基于记忆启发的强化学习方法研究

刘晓峰,刘智斌,董兆安

(1.曲阜师范大学 图书馆,山东 日照 276826;2.曲阜师范大学 计算机学院,山东 日照 276826)

0 引 言

强化学习[1-2]是机器学习的一个重要分支,它的基本思想来源于心理学和生物学,在计算机科学、决策理论以及控制工程等领域得到了普遍重视,其应用范围也越来越广泛。采用强化学习方法,不需要进行显式编程,Agent在一定的环境中,其每一步都收到一个报酬值,强化学习方法试图通过学习得到报酬值最大的策略。然而采用传统的强化学习算法,收敛速度是很慢的,例如：从目标状态将报酬值传递到较远的状态需要无数次的迭代。对于大型状态空间,由于存在“维数灾难”,使采用强化学习的方法进行求解几乎成为不可能。为了提高学习效率,人们不断探索各种方法。Sutton等[3]提出了Option方法,他们将状态空间分解为若干个子集,采用分而治之的策略进行求解。Parr R[4]提出了HAM方法,他将每个子任务抽象为一个建立在MDP上的随机有限状态机。Bernhard Hengst[5]提出了HEXQ方法,他利用时域和状态抽象的方法生成小规模的状态变量子空间。Thomas G. Dietterich[6]提出了MAXQ方法,这种方法则将动作序列或动作集进行分组,将强化学习中的单步决策扩展到多步决策,减少了决策次数。Hashemzadeh等人[7]提出将具有相似策略的状态分类到同一个集群中,并且通过这种定位,Agent可以更多地利用子空间学习的泛化,有效地提高了学习效率。

以上方法将大问题划分为较小问题来解决,同时也使简单问题复杂化。强化学习中Agent的学习是盲目的,没有任何先验知识,学习过程全靠其不断摸索,这样势必造成学习效率较低,难以应用到实际问题中。人们开始用间接知识指导Agent的探索行为,减小问题的搜索域,从而提高学习效率。Peter Dayan等[8]提出了Feudal方法,简单地将一个迷宫问题由下往上进行聚合,上层作为下层的管理者,这样Agent的学习有了指导,效率有了提高。Shi等人[9]提出了一种高效的模糊规则分层强化学习算法(HFR),这是一种将人的先验知识与分层策略网络相结合的新框架,可以有效地加速策略的优化。Cai等人[10]增强了启发式算法的能力,以贪婪地改进RL生成的现有初始解,并展示了新颖的结果,其中RL能够利用启发式的性能作为学习信号来进行更好的初始化。

在不具有先验知识或先验知识不够明晰的情况下,还要靠Agent自我学习。其实,Agent在每一轮学习过程中也是在不停地获得经验知识,希望Agent在不具有先验知识或拥有先验知识较少时,也能利用自身学习的经验提高效率。该文提出一种基于记忆启发的强化学习方法,不需要植入先验知识,自主Agent能将学习中获得的知识作为启发知识应用到以后的学习中,利用启发式Shaping回报函数改造Q学习方法,使Agent在一定程度上脱离盲目探索,以提高效率。

1 强化学习机制

强化学习与监督学习和无监督学习不同,它强调在环境中交互学习,通过在学习过程中取得的评价性的反馈信号作为回报,在学习过程中,通过最大化其积累回报,选取最优行为[11]。

Qπ(s,a)=E{rt+1+γrt+2+γ2rt+3+…

|st=s,at=s,π}

(1)

其中,0<γ<1。

进而求得状态行为对的Q值为：

(2)

对于状态s,定义：

若环境模型和转移概率为已知,上述问题归结为动态规划问题。然而,在实际应用中,环境模型和转移概率往往不可知。针对这个问题,Watins[14]提出了Q学习算法同时证明了它的收敛性。表示为：

Q(s,a))

(4)

其中,0<γ<1。

Agent在每次迭代中更新Q(s,a)值,在多次迭代后Q(s,a)值收敛。

有了上述关于Q值的定义,很容易通过策略迭代得到V*值和最优策略π*,表示如下：

(5)

(6)

2 启发式Shaping回报函数

Agent在学习中从环境中获得报酬值,以更新当前的Q值或V值。在Agent学习过程中,提供附加的报酬值将会有效地提高学习性能,这种思想被称为Shaping[15]。若提供一个合适的启发回报函数：F(s,a,s'),则式(4)改写为：

Q(st+1,at+1)=Q(st,at)+α(r+F(s,a,s')+

(7)

一个学习策略的选择就从一个马尔可夫决策过程M=(S,A,T,γ,R)转换为在M'=(S,A,T,γ,R')中学习优化策略。其中：R'=R+F为新定义的报酬值。假如在马尔可夫决策过程M=(S,A,T,γ,R),Agent从状态s到s'从环境得到报酬为R(s,a,s'),那么在新的马尔可夫决策过程M'=(S,A,T,γ,R'),Agent收到的报酬为：R(s,a,s')+F(s,a,s')。

定义1：在马尔可夫决策过程中,已知S,A,γ,给定一个Shaping回报函数F：S×A×S|→R。令F(s,a,s')=γφ(s')-φ(s),其中：φ(s)和φ(s')分别为状态s和状态s'下的势场函数。

推论1：在一个Shaping回报函数启发的马尔可夫决策过程中,M=(S,A,T,γ,R)转化为M'(S,A,T,γ,R'),其中：γ'(s,a,s')=r(s,a,s')+F(s,a,s')。Shaping回报函数为：F：S×A×S|→R。

定理1：如果F是一个基于势场函数的Shaping函数,F(s,a,s')=γφ(s')-φ(s),则在M'(S,A,T,γ,R')中的优化策略在M=(S,A,T,γ,R)中也必为优化策略。

证明：对于M有：

-φ(s)=

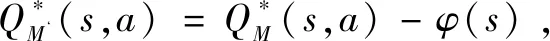
(8)

定理2：如果F是一个基于势场函数的Shaping函数,F(s,a,s')=γφ(s')-φ(s),则在M=(S,A,T,γ,R)中的优化策略在M'(S,A,T,γ,R')中也必为优化策略。

证明思路与定理1类似。

3 算法实现

标准的强化学习方法都是通过探索-利用过程以发现搜索目标,然而在找到目标后,又开始了新的探索过程,使得原来获得的经验结果大部分被遗忘。

对于Agent,给定一个初始状态,让它不断学习,当它到达目标后,记下目标的位置goal,然后围绕goal形成一个势能场,为以后的Agent学习提供了一个启发势场函数。势场函数定义为：

φ(s)=λh(s,goal)

(9)

其中,s为当前状态,λ为启发强度因子,势场函数形式视具体问题而定。

算法描述如下：

初始化Q(s,a);

从状态s开始搜索,经过一个episode(轮),直到发现目标goal,记录下goal的状态;

for each episode

{

选择状态s∉goal;

While(没有满足终止条件)

{

计算φ(s);

从当前状态s下按某种策略(如：ε-greedy)选择行为a;

执行行为a,获得报酬值rt,进入到下一状态s';

计算φ(s');

根据收敛情况,采取某种方法(如：模拟退火法)选择学习率α;

计算F(s,a,s');

更新Q值：

}

}

4 实验与结果分析

4.1 实验环境

算法采用路径规划问题作为一个算例(如图1所示),实验环境采用一个30×30的网格,图中S为Agent所处的初始位置,G为目标点。图中白色的部分为Agent的自由活动区域,灰色的区域为障碍物,四周为墙壁,Agent不能穿过墙壁也不能穿过障碍物。假定Agent能感知自身所处的位置,但它起初对环境的一无所知。该问题是让Agent以尽可能短的时间,搜索到一条通往G点的最短路径。

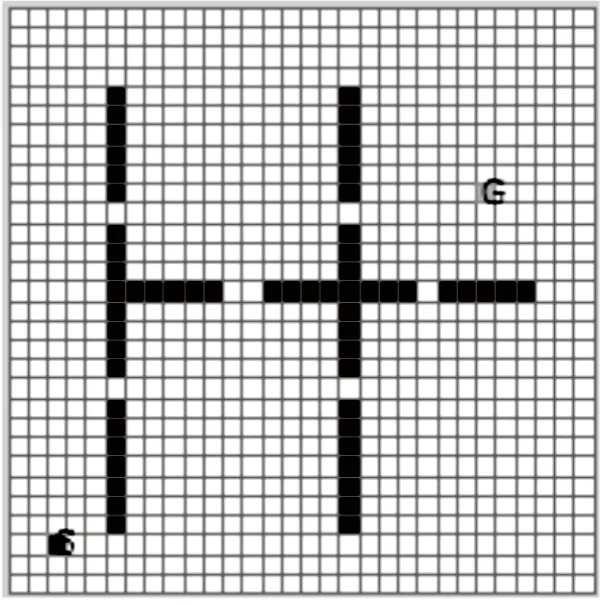
图1 一个路径规划实例

显然,该问题是无法用Dijkstra或A*等算法解决的,因为对Agent来说环境是未知的。Agent通过不断地学习,探索一条合适的通向G点的优化路径。

采用Q学习方法,Agent在任意状态s可选的行为集合为：{向上,向下,向左,向右}。

实验参数设置为：初始学习率α=0.1,折扣因子γ=0.95,采用ε-greedy方法选择优化行为,ε=0.1。

Agent被盲目地置于任何合法位置而开始学习,Agent的测试源坐标定义为[2 2],目标坐标定义为[24 20]。

报酬值设定为：若Agent到达目标G,将从环境获得100的奖赏;若Agent撞到墙壁上将退回到原处,奖惩值为0;Agent每移动一步将获得-1的惩罚。

4.2 采用标准Q学习的学习性能

采用标准的Q学习算法进行训练。在每轮学习中,设置Agent的搜索步数上限为3 000,超过3 000步还找不到目标点,本轮搜索就失败,开始新一轮的搜索。从图2发现,随着不断地学习,每一轮的学习时间在逐步缩短。当Agent学习了599轮,测试从S点到G点的学习结果如图3所示,可见Agent从测试点出发能搜索到目标点,但是仍然走了若干冗余步,获得的路径还不是最优的,若想得到最优结果还需继续学习。

图2 Q学习每轮步数

图3 用Q学习实现路径规划

4.3 基于记忆启发的学习性能

Agent在学习过程中搜索到目标,记下目标点位置,以此为依据进行启发搜索,启发势场函数为：

φ(s)=

(10)

其中,λ为启发因子,λ>0。

Shaping函数为：

F(s,a,s')=γφ(s')-φ(s)

(11)

其中,γ为折扣因子,取值0.95。

在实验中,令λ=0.3,实验结果如图4、图5所示,设定学习轮数为300。由结果可见,因为加入了启发函数,收敛速度较没有启发的Q学习算法快了很多,但是还是有冗余步,分析原因为：采用该文定义的势能场函数,离目标越远,Agent可选的几个行为所得的启发回报值F区别越不明显,其学习效果与没有启发的Q学习越接近;反正,离目标点越近,启发效果越明显。

图4 启发Q学习(λ=0.3)每轮步数

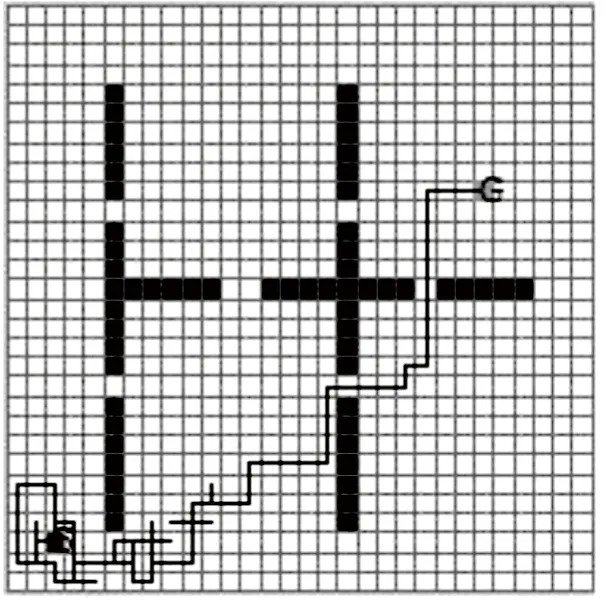
图5 用启发Q学习(λ=0.3)实现路径规划

为了提高启发效果,在实验中,令λ=0.8,实验结果如图6、图7所示,学习轮数在75左右,算法就能达到收敛,并且Agent在测试点能搜索到最优路径。由结果可见,适当提高启发因子,有利于Agent快速找到目标。

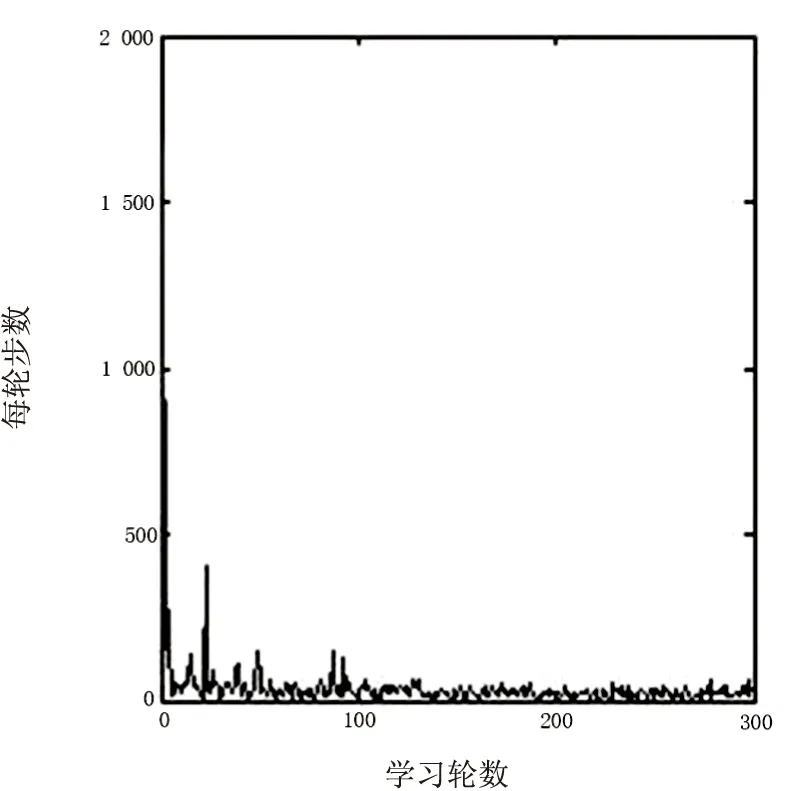
图6 启发Q学习(λ=0.8)每轮步数

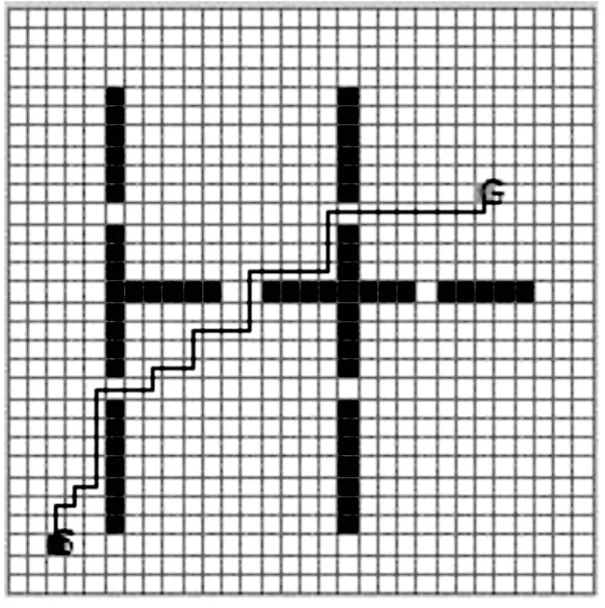
图7 用启发Q学习(λ=0.8)实现路径规划

令λ=1.6,做了同样的实验,实验结果如图8、图9所示。由结果可见,Agent能很快发现最优路径,但是也发现在学习中出现了一些“死点”,Agent一旦陷入到这些点往往不能自拔,当学习步数达到3 000,当前轮就被强制终止,这种现象是由于“过启发”造成的。现分析如下：

图8 启发Q学习(λ=1.6)每轮步数

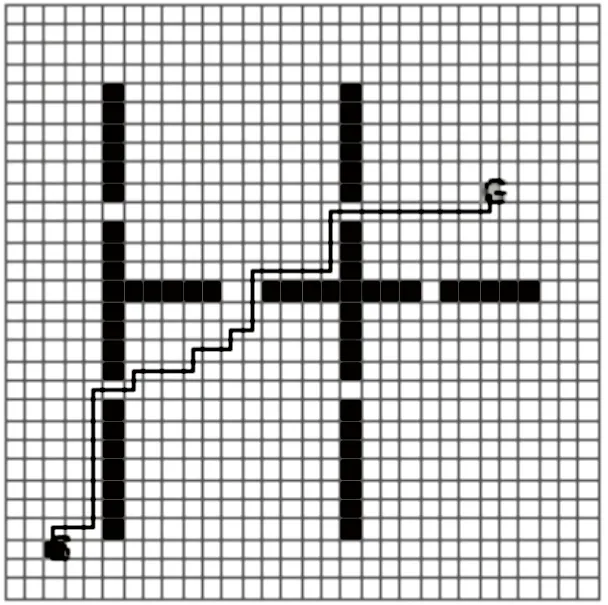
图9 用启发Q学习(λ=1.6)实现路径规划

在F(s,a,s')=γφ(s')-φ(s)中,若Agent从某s点执行行为a碰壁后又回到s点,也就是s=s',于是有：F(s,a,s')=F(s,a,s)=γφ(s)-φ(s)=φ(s)(γ-1),又因为φ(s)<0,γ-1<0,所以F(s,a,s)>0。而λ越大,则启发值F也就越大,造成Q(s,a)越大,并不断积累。以后Agent在状态s下,选择行为a的概率将不断加大。在以后的学习中,这个Q(s,a)会把值向周围状态扩散,于是s状态就变成一个“死点”或伪目标,致使Agent走到这个区域便陷入并无法逃脱。针对这个问题,该文提出一种修改回馈报酬的方法,检测Agent的行为和新的状态,一旦发现Agent陷入死点,就对这个状态-行为对的Q值增加一个惩罚值,惩罚值的大小视Agent陷入的深度而定,这样随着Agent不断学习,会跳出这个死点到别处进行探索。经这种方法处理后,实验表明：死点被较理想地消除了。

通过以上分析可以看出,应选择合适的λ值。λ值太小,启发效果不明显;启发太大,易产生死点。

5 结束语

无须先验知识为指导,Agent在发现目标后,基于目标位置,再进一步搜索优化策略,这样Agent的搜索将不再盲目。该文构造了一个基于势能场的启发函数,利用Shaping回报函数,以路径规划问题作为一个算例,证明基于记忆启发的强化学习算法能大大提高学习效率。

针对不同的问题,势能场启发函数可以有多种不同的构造方法,相应启发因子的选取也是一个需要进一步讨论的问题。另外,Agent在搜索中除了以目标位置作为启发,在其学习过程中所得到的过程知识也可以作为启发知识加入到以后的学习过程中,这也是本课题需要继续研究的问题。在多Agent的环境中,Agent可以利用自己学习到的知识,也应该能利用其它Agent所学到的知识。该文提出的方法可以应用到许多领域[16],比如路由问题、资源分配、搜索问题、web服务组合、数据挖掘、机器人以及网络拓扑优化等,都有望得到较好的结果。