连通子集性质的推广与等价刻画
黄 瑞
(阜阳师范大学 数学与统计学院,安徽 阜阳 236037)
集合上赋予一个拓扑就得到了该集合上的一个拓扑空间,一个集合上可以定义若干个不同的拓扑空间,如3个点的集合上能定义29个拓扑,在不区分同胚的情况下,这29个拓扑空间共分成9类,每一类的结构和拓扑性质各不相同。一般地,对一个拓扑空间的研究往往是从研究该空间中的特殊子集开始的,如邻域、导集、闭包等概念的“源头”都是拓扑空间中的特殊子集“开集”,局部连通空间的“源头”是拓扑空间中的特殊子集“开集”和“连通子集”,局部道路连通空间的“源头”是拓扑空间中的特殊子集“开集”和“道路连通子集”。连通子集是拓扑空间中的一类特殊子集,很多文献中都阐述了连通子集的性质,[1-7]给出了连通子集的一些重要性质,如文中预备知识中的引理2-5,除此之外一般文献中还会给出连通子集的其他一些重要性质,如若一个子集被“夹在”了一个连通子集和其闭包之间,则这个子集也是连通子集。
关于连通性的研究有很多,文献[8]研究了连通子集的充要条件,[9]研究了一类正弦曲线的连通性,[10]则研究了一般拓扑空间的连通性,其中给出了二维欧氏平面中所有至少有一个坐标为有理数的点的全体构成的集合是一个连通子集的结论,[11]和[12-13]分别研究了点集拓扑中的连通性和子基的连通性,[14-20]则研究了特殊拓扑空间的一些特殊连通性。本文将进一步研究连通子集的性质。
1 预备知识
定义1[1]已知拓扑空间(X,Γ),若(X,Γ)中存在两个非空的隔离子集A,B,且满足A⋃B=X,则称拓扑空间(X,Γ)是不连通空间,否则称(X,Γ)是连通空间。
定义2[1]已知Y是拓扑空间(X,Γ)的子集,若Y作为(X,Γ)的子空间是连通空间,则称Y是拓扑空间(X,Γ)的连通子集,否则称Y是拓扑空间(X,Γ)的不连通子集。
引理1已知拓扑空间(X,Γ),A⊂Y⊂X,则A是(Y,Γ|Y)的连通子集 ⇔A是(X,Γ)的连通子集。
证 明A是(Y,Γ|Y)的通子集 ⇔(A,Γ|Y|A)=(A,Γ|A)是连通空间 ⇔A是拓扑空间(X,Γ)的连通子集。
引理2[1]设{Yγ}γ∈Γ是拓扑空间X的连通子集族,且,则是X的连通子集。
引理3[1]设C是拓扑空间X的连通分支,则
(1)若Y是X的连通子集,且Y⋂C≠∅,则Y⊂C;
(2)C是拓扑空间X的连通的闭集。
引理4[1]设Y是拓扑空间X的连通子集,A,B是拓扑空间X的隔离子集,且Y⊂A⋃B,则或者Y⊂A或者Y⊂B。
引理5[1]已知拓扑空间X,则下列条件等价
(1)拓扑空间X是不连通空间;
(2)拓扑空间X存在两个非空的闭集A,B,满足A⋃B=X,A⋂B=∅;
(3)拓扑空间X存在两个非空的开集A,B,满足A⋃B=X,A⋂B=∅;
(4)拓扑空间X存在既开又闭的非空真子集。
引理6已知拓扑空间(X,Γ),A⊂Y⊂X,则
(1)若(Y,Γ|Y)是(X,Γ)的开子空间,则A是(Y,Γ|Y)的开集⇔A是(X,Γ)的开集;
(2)若(Y,Γ|Y)是(X,Γ)的闭子空间,则A是(Y,Γ|Y)的闭集⇔A是(X,Γ)的闭集。
证明(1)若A是(Y,Γ|Y)的开集,则存在(X,Γ)中的开集U使得A=U⋂Y,又Y也是(X,Γ)中的开集,故A=U⋂Y是(X,Γ)中的开集;
若A是(X,Γ)的开集,则A⋂Y=A就是(X,Γ)的子空间(Y,Γ|Y)的开集。
同理可得(2)的证明。
引理7设A,B是拓扑空间(X,Γ)中的隔离子集,若A⋃B是拓扑空间X的开集(闭集),则A,B是拓扑空间X的开集(闭集)。
证明若A,B中有一个是空集,则结论显然成立。下设A,B≠∅,令Y=A⋃B,则拓扑空间(X,Γ)的子空间(Y,Γ|Y)是不连通空间。
若Y=A⋃B是(X,Γ)中的开集,由引理 5的证明过程知A,B是开子空间(Y,Γ|Y)中既开又闭的非空真子集,再由引理6知A,B是拓扑空间(X,Γ)中的开集。
同理,若Y=A⋃B是(X,Γ)中的闭集,则A,B是拓扑空间(X,Γ)中的闭集。
2 连通子集两条性质的推广
由定义1知判断拓扑空间X是否是连通空间的一个重要思路是将X表示成两个隔离子集A,B的并,即X=A⋃B,然后通过已知条件确定A,B是否非空。若A,B都非空,则拓扑空间X是不连通空间,若A,B有一个非空,另一个是空集,则X是连通空间。引理2正是用上面的思路给出的证明,事实上引理2中“交集非空的连通子集族”这个条件可放宽,引理2可以推广成下面的定理1。
定理1设{Yr}r∈Γ是拓扑空间X的连通子集族,∀α,β∈Γ,在指标集Γ中有有限个元素γ1=α,γ2,…γn,γn+1=β,使得与Yγi+1不隔离,则是X的连通子集。
证明设,其中A,B是拓扑空间X中的隔离子集。∀α∈Γ,则Yα是拓扑空间X的连通子集,且Yα⊂A⋃B,由引理 4知要么Yα⊂A,要么Yα⊂B。
不失一般性设Yα⊂A,则∀β∈Γ,在指标集Γ中有有限个元素γ1=α,γ2,…γn,γn+1=β,使得∀i=1,2,…,n,都不隔离。
综上,∀α∈Γ,不失一般性设Yα⊂A,则∀β∈Γ,都有Yβ⊂A,故即从而得到是拓扑空间X中的连通子集。
定理1给出了连通子集的并仍是连通子集的一个充分条件。事实上,连通子集的交也未必是连通子集,如在有限补空间R中,A={-1,0,1,2,…},B={1,0,-1,-2,…}都是连通子集,但A⋂B={-1,0,1}却不是有限补空间R中的连通子集。
引理4中连通子集包含在两个隔离子集的并之中,这“两个隔离子集”可放宽松为“两个无交的开(闭)集”,结论仍然成立,引理4可推广成下面的定理2。
定理2设Y是拓扑空间(X,Γ)的非空连通子集,A、B是拓扑空间X中的无交开(闭)集,且Y⊂A⋃B,则或者Y⊂A或者Y⊂B。
证明若A,B是拓扑空间(X,Γ)中的无交闭集,则A,B就是拓扑空间X中的隔离子集,由引理4知结论成立。
下设A,B是拓扑空间(X,Γ)中的无交开集,则A⋂Y,B⋂Y就是连通空间(Y,Γ|γ)中的开集,且(A⋂Y)⋂(B⋂Y)=∅,(A⋂Y)⋃(B⋂Y)=(A⋃B)⋂Y=Y。由引理5知,要么A⋂Y=∅,要么B⋂Y=∅。
若A⋂Y=∅,则B⋂Y=Y,即Y⊂B;若B⋂Y=∅,则A⋂Y=Y,即Y⊂A。
3 连通子集和不连通子集的等价刻画
由定义2知连通子集作成的子空间是连通空间,因此连通空间具有的性质连通子集也必定满足,而由引理5可得拓扑空间是连通空间的充要条件是该拓扑空间中既开又闭的子集只能是空集和全集,于是得到下面的定理。
定理3Y是拓扑空间(X,Γ)的连通子集⇔(Y,Γ|Y)中既开又闭的子集只有∅和Y。
定理4设Y是拓扑空间(X,Γ)的一个包含多于1个点的子集,则Y是拓扑空间(X,Γ)的连通子集⇔Y中的任意两个点在(Y,Γ|Y)中是连通的。
证明充分性。取a∈Y,∀y∈Y,则a,y在(Y,Γ|Y)中是连通的,即在 (Y,Γ|Y)中存在连通子集Yay,使得a,y∈Yay⊂Y。
必要性。(Y,Γ|Y)是连通空间,则 (Y,Γ|Y)中任意两个点在(Y,Γ|Y)中都是连通的。
由定理4易见拓扑空间X是连通空间的一个充要条件是拓扑空间X中的任意两个点在拓扑空间X中是连通的,这是连通空间的一个“正面”的等价刻画。
定理5设Y是拓扑空间(X,Γ)的一个子集,则Y是拓扑空间(X,Γ)的不连通子集⇔存在(X,Γ)的开集(闭集)A,B,使得Y⊂A⋃B,A⋂B⊂X-Y,A⋂Y≠∅ ,B⋂Y≠∅成立。
证明必要性。拓扑空间(Y,Γ|Y)是不连通空间,由引理5得,存在(Y,Γ|Y)中的非空开集(闭集)AY,BY,使得AY⋃BY=Y,AY⋂BY=∅。从而存在(X,Γ)中的开集(闭集)A,B,使得A⋂Y=AY,B⋂Y=BY。
易见
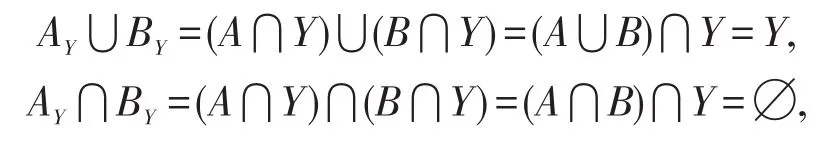
从而得到

成立。
充分性。由条件知A⋂Y,B⋂Y为拓扑空间(Y,Γ|Y)中的非空开集(闭集),且满足
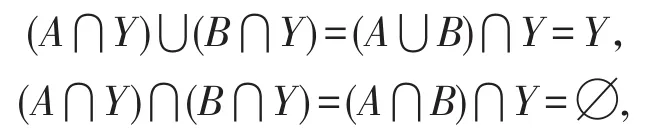
由引理5得,Y是(X,Γ)的不连通子集。
易见当定理5中的Y=X时,定理5就变成了引理5,因此从这个意义上来说,定理5可看成是引理5的一个推广。
定理6设Y是拓扑空间(X,Γ)的一个子集,则是拓扑空间(X,Γ)的不连通子集⇔ 存在(X,Γ)的非空子集A,B,使 得,A⋂Y≠∅ ,B⋂Y≠∅ 成立。
证明必要性。由拓扑空间是不连通空间知,存在(X,Γ)中的非空隔离子集A,B,且,即Y⊂A⋃B成立。
若A⋂Y=∅,由(A⋂Y)⋃(B⋂Y)=(A⋃B)⋂Y=Y,得到B⋂Y=Y,即Y⊂B,则,从而得到。
由定理5知是(X,Γ)的不连通子集。
4 连通子集与既开又闭的子集之间的关系
连通子集和既开又闭的子集都是拓扑空间中的特殊子集,由引理5知两者之间存在着“密切”的关系,下面将进一步研究两者之间的关系。
定理7设Y是拓扑空间(X,Γ)的连通子集,B是拓扑空间(X,Γ)的既开又闭的子集,则或者Y⋂B=∅,或者Y⋂B=Y。
证明B⋂Y是拓扑空间(X,Γ)的子空间(Y,Γ|Y)中既开又闭的子集,且(Y,Γ|Y)是连通空间,由引理5知,若Y⋂B≠∅,则必有Y⋂B=Y。
定理8拓扑空间中既开又闭的非空连通子集必是该拓扑空间的连通分支。
证明设B是拓扑空间(X,Γ)中的既开又闭的非空连通子集,取a∈B⊂X,设a在拓扑空间(X,Γ)中所在的连通分支为C。
一方面,B是拓扑空间(X,Γ)中的连通子集,且B⋂C≠∅,由引理3知,B⊂C;另一方面,由引理3知,连通分支C是拓扑空间(Y,Γ)中连通子集,C⋂B≠∅ ,由定理 7知,C⋂B=C,即B⊃C。综上B=C,结论得证。
5 小结
连通子集是拓扑空间中的一类重要的特殊子集。文中首先推广了[1]中的连通子集的两条重要性质,定理1推广了引理2中连通子集的并仍是连通子集的充分条件,定理2推广了引理4中的结论;其次给出了连通子集的两个等价刻画,不连通子集的两个等价刻画;最后研究了拓扑空间中连通子集与既开又闭的子集之间的关系。另外,文中还给出了拓扑空间中连通子集的交不是连通子集的一个具体的例子。

