偏序集的序连通关系及其序连通分支

唐照勇

(扬州大学 广陵学院,江苏扬州 225000)

§1 引言

偏序集刻画了事物的顺序特征,连通性是偏序集理论重要研究内容.元素间连通具有很强的直观性,表现为其Hassse图两个元素都是相连的.文献[1]阐述了序连通概念,即任意两个元素间可以找到有限多个元素,使得这些元素间是依次可比地.唐照勇等在文献[2-4]中也研究了偏序集的连通性,不过构造的集列中每个步集(除了第一个步集外)既是上升集,也是下降集.在此基础上,本文以上集列为工具,构造上集列连通分支来刻画偏序集的连通性,提供描述偏序集连通性的新方法及新形式.由此得到许多良好的结论,并且由此可知,刻画偏序集连通性的途径可以是多样地.

§2 预备知识

定义2.1[1]设E是一个非空集合.如果R是E上的一个二元关系并满足下面条件(1)-条件(3),则称R是E的序关系.

(1) 自反性: (∀x ∈E)xRx;

(2) 反对称性: (∀x,y ∈E)若xRy,yRx,则x=y;

(3) 传递性: (∀x,y,z ∈E)若xRy,yRz,则xRz.

通常把这样的一个序关系R写为≤(称为小于或等于).称赋予序≤的集合E为偏序集,记为(E,≤).

定义2.2[1]设(E,≤)是偏序集,D是E的非空子集.定义D上的一个序关系

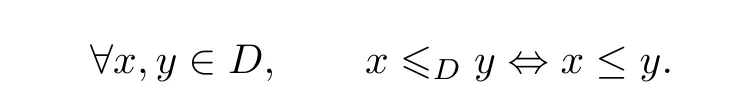
则(D,≤D)是一个偏序集,称为(E,≤)的子偏序集.

定义2.3[1]设(E,≤)是偏序集,D是E的非空子偏序集.若对任意x ∈D和任意y ∈E,y ≤x蕴含y ∈D,则称D是E的一个下降集;对偶地,称D是E的一个上升集,如果对任意x ∈D和任意y ∈E,y ≥x蕴含y ∈D.

定义2.4[1]设(E,≤)是偏序集,若对任意x,y ∈E,inf{x,y}和sup{x,y}在E中存在,则称E是一个格.

定义2.5[5]设f:是一个保序双射.如果f的逆映射f-1:也是保序映射,那么称f是保序同构映射,并称偏序集E和F是保序同构,记为.

引理2.1[5]设(E,≤)是偏序集,H是E的非空子集.则H是上升(下降)集当且仅当

其中↑H={x ∈E |x ≥y,y ∈H},↓H={x ∈E |x ≤y,y ∈H}.

引理2.2设(E,≤)是偏序集,A,B是E的非空子集.则有

由此引理,易得下列推论.

推论设(E,≤)是偏序集,A,B是E的非空子集.若B ⊆A,则有

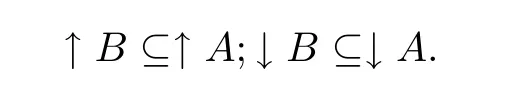
引理2.3[1]设E,F是偏序集.则f:是一个保序同构映射当且仅当下面的条件成立.

(1)f是满射;(2) (∀x,y ∈E)x ≤y ⇔f(x)≤f(y).

§3 上集列与上集列连通分支

定义3.1(上集列)设(E,≤)是偏序集,a ∈E.按以下步骤操作.

定义3.2(上集列连通分支)设(E,≤)是偏序集,a ∈E,是上集列.记

则称[↑a]为元素a的上集列连通分支.在不引起混乱的情况下,简称连通分支.本文中所提到的连通分支都是指上集列连通分支.

定理3.1设(E,≤)是偏序集,a,b ∈E.a ∈[↑b]的充要条件是存在有限个元素

注1定理结论中(2)式和(3)式是可以相互转化的.例如当n是一个偶数时,结论(2)的形式

也可以写成(3)的形式

因而无论采用哪种形式来说都不影响定理的正确性.

注2这些有限个元素xi ∈[↑b],i=1,2,···,n.这由定理的证明过程容易得到.

§4 刻画连通性

下面将利用上集列连通分支来刻画偏序集的连通性.

定义4.1(连通)设(E,≤)是偏序集,x,y ∈E.若存在一个连通分支[↑a],使得x,y ∈[↑a],则称x和y在E上是连通的,简称x和y连通,记作x～y,也就是说属于同一个连通分支的两个元素是连通的.

定理4.1设(E,≤)是偏序集,a,b ∈E.若[↑a]∩[↑b]∅,则[↑a]=[↑b].

证假设[↑a]∩[↑b]∅,则存在e ∈E,使得e ∈[↑a]且e ∈[↑b].任取x ∈[↑a],下证x ∈[↑b].

依据定理3.1必要条件可知,存在有限个元素

将这些元素合起来便有p+m+n个元素使得(相同元素重复计算)

在依据定理3.1充分条件可知x ∈[↑b],故[↑a]⊆[↑b].同理可证[↑b]⊆[↑a],所以[↑b]=[↑a].

连通关系构成了偏序集元素间的一个关系,而且这个关系是一个等价关系.

定理4.2偏序集的连通关系是一个等价关系.

证设(E,≤)是偏序集,x,y,z ∈E.

(1) 显然连通关系～满足反身性: 因为x ∈[↑x],故x～x;

(2) 满足对称性: 假设x～y,由连通定义知存在一个连通分支[↑z],使得x,y ∈[↑z],故y～x;

(3) 关系满足传递性: 假设x～y,y～z.由连通定义知存在连通分支[↑a],[↑b],使得

从而[↑a]∩[↑b]∅,故[↑a]=[↑b].所以x,z ∈[↑b],即x～z.

由近世代数[6]知识可知,一个等价关系必然形成一个分类.必须指出的是上述连通分支就是分类中的一个类,即有如下结论.

定理4.3设(E,≤)是偏序集,a ∈E.则[↑a]=[a](其中[a]是一个类).

证设类[a]={x|x～a}.

由x～a知,存在一个连通分支[↑c],使得x,a ∈[↑c].则a ∈[↑a]∩[↑c]∅,故[↑a]=[↑c],x ∈[↑a].由x的任意性可知,

此定理揭示了由连通关系产生的类具体的构造,即每一个类都是一个连通分支.这样就不难得到下述定理.

定理4.4设(E,≤)是偏序集,a,b ∈E.a ∈[↑b]当且仅当a～b.

由定理3.1,定理4.4立马可得下述定理.

定理4.5设(E,≤)是偏序集,a,b ∈E.a～b当且仅当存在在有限个元素

另外依据定理4.1还可得下面结论.

定理4.6 设(E,≤)是偏序集,a,b ∈E.a ∈[↑b]当且仅当[↑a]=[↑b].

证(必要性)由a ∈[↑b]且a ∈[↑a]知[↑a]∩[↑b]∅,从而[↑a]=[↑b].

充分性显然.

§5 连通子集

定义5.1 设(D,≤D)是偏序集(E,≤)的非空子偏序集,如果D中任意两个元素在(D,≤D)上都是连通的,称D是E的连通子集.否则称D为不连通子集.特别地,若E是连通的,则称偏序集(E,≤)是连通偏序集;若E是不连通的,则称偏序集(E,≤)是不连通偏序集.

值得注意的是,子偏序集上的连通概念,也是在子偏序集上相应的定义步集,上集列,上集列连通分支等概念基础上的.这里就不赘述了.

定理5.1格都是连通偏序集.

由此定理可知,格的连通分支只有一个,就是其本身.事实上,任何一个连通偏序集的连通分支都只有一个,就是其本身.反过来,有且仅有一个连通分支的偏序集必是连通偏序集.

下例指出一个事实,偏序集中的两个元素在此偏序集中是连通的,但是在子偏序集中可能是不连通的.反过来,如果两个元素在子偏序集中连通,必然在偏序集中连通,这点可由定理4.5得知.

例1设(E,≤)是偏序集,其Hasse图如下图1-1所示.

图1-1 (E,≤)

易得由元素a产生的上集列

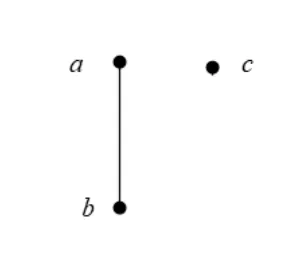
图1-2 (D,≤D)

定理5.2设(E,≤) 是偏序集,a ∈E.则连通分支[↑a]是E的连通子集.

证设b,c ∈[↑a],即b～c.下证b和c在子偏序集([↑a],≤[↑a]) 上也是连通的.一方面,依据定理4.5必要条件,由b～c可知,存在有限个元素

由定理3.1的注2知xi ∈[↑b](i=1,2,3···n).

另一方面,依据定理4.6,由b ∈[↑a]得[↑a]=[↑b],故xi ∈[↑a](i=1,2,3···n).再依据定理4.5充分条件知在子偏序集([↑a],≤[↑a])上b,c之间也是连通的.所以连通分支[↑a]是E的连通子集.

由定理4.3和定理5.2可知

推论1连通分支[↑a]是含元a的最大连通子集.

定理5.3设(E,≤)是偏序集,则E可以唯一分解为一些连通分支的不交并.

证一方面,取a ∈E,有a ∈[↑a],即对于E中每个元素,都存在某一个连通分支使得该元素属于这个连通分支;

另一方面,设a ∈[↑x],a ∈[↑y],则由定理4.1可知[↑x]=[↑y],即每个元素不能同时属于两个不同的连通分支,也就是说只能属于一个连通分支.综上可知,对于E中每个元素有且只能属于一个连通分支.故

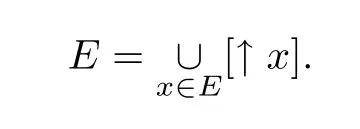
定义5.2设H是偏序集(E,≤)的非空子集.若H=↑H=↓H,则称H是分支并,即分支并既是上升集又是下降集.

下述定理揭示了连通分支应该满足的特征.

定理5.4设H是偏序集(E,≤)的非空子集.则H是E的连通分支当且仅当H既是分支并又是连通子集,简称连通分支并.

证必要性 设a ∈E,不妨令H=[↑a],即H是E的连通分支.由定理5.2可知H是连通子集.下证H是分支并.

设b ∈H,x ∈E,x ≤b.则∃n ∈N+,使得于是必有

由此可知H是下降集.同理可证H是上升集,所以H是分支并.必要性得证.

充分性 设H是一个连通分支并,a ∈H.由预备知识中的推论,有

以此类推下去知对任意n ∈N+,都有,从而,即连通分支[↑a]⊆H.下证[↑a]=H.

定理5.5在保序同构映射下,连通子集的像(原像)也是连通子集.

证一方面,设f:是一个保序同构映射.其中H是偏序集(E,≤E)的非空连通子集,下证像f(H)是偏序集(F,≤F)的连通子集.

任取x,y ∈f(H),则有唯一元a,b ∈H使得a=f-1(x),b=f-1(y).依据定理4.5,由a～b可知存在有限个元素

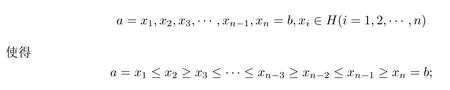
依据引理2.3知在f(H)中必存在唯一一些元素

从而x与y在f(H)上连通,故f(H)是连通子集.

另一方面,设H是偏序集(F,≤F)的非空连通子集,类似证明可得原像f-1(H)是偏序集(E,≤E)的连通子集.

另外,不难验证在保序同构映射下,上升集的像(原像)也是上升集,下降集的像(原像)也是下降集.于是结合定理5.5可知,连通分支并的像(原像)也是连通分支并.最后再由定理5.4可得下列结论.

定理5.6在保序同构映射下,连通分支的像(原像)也是连通分支.

最后指出,就(序)连通关系和(序)连通分支而言,偏序集与其对偶偏序集是“等同”的.