一类特殊笛卡尔乘积网络的泛圈性

张治成

(石河子大学 理学院,新疆石河子 832003)

§1 引言

互连网络是超级计算机的重要组成部分,在很大程度上决定着超级计算机的性能,其拓扑结构是指超大规模计算机系统中的元件(处理器)的连接模式.互连网络的结构和性质是超级计算机研究的重要课题.在设计和选择一个互连网络的拓扑结构时,Hamilton性,泛圈性,连通度,直径等指标对分析网络性能发挥了重要作用.

在分析网络拓扑结构时,通常将互连网络拓扑结构模型化为一个无向图,图的顶点对应处理器,图的边对应网络的通讯链路[1-4].因而在研究互连网络的拓扑结构时,往往通过研究一个无向图来深入研究互连网络.互连网络拓扑的性能可以通过图的性能和指标来度量,如Hamilton性,嵌入性,容错性,泛圈性等[1-12].因此,图论是设计和分析互连网络最基本且强有力的工具.

图嵌入是一个客图到一个主图的映射,它保留了一些被要求的性质.如果一个客图能够嵌入到一个主图,那就意味着在客图网络上能够执行的算法同样能够在主图网络上模拟执行.在众多的互连网络拓扑中,路和圈是最为基础,也是最为重要的两种网络拓扑结构.在路和圈网络中,容易设计出简单而又高效的路由算法.因此,在设计和选择互连网络时路和圈的可嵌入性是一个非常重要的考虑因素.近年来,Bondy提出了泛圈性问题,即寻找所有可能长度的圈[1].泛圈性是判断一个网络拓扑是否适合将不同长度的圈映射到其上的重要测量值.圈的嵌入是对互连网络的图嵌入问题研究的重点之一,它可以用图的泛圈性和边泛圈性来衡量.

在大规模并行系统中,互连网络在硬件成本,通信性能,高效算法和容错能力方面扮演着重要的角色.近年来,学者们提出了许多互连网络拓扑.笛卡尔乘积网络DSCC(k)×K2是师海忠等提出的一类重要的互连网络拓扑[5-6],由于它具有较好的正则性,连通性,Hamilton性等性质,从而为大规模超级计算机系统和互连网络的优化设计提供了理论参考价值,得到了广泛的关注和研究.

§2 预备知识

下面介绍文中用到的一些基本知识.

定义2.1[1-2]设G=(V,E)是一个图,下述概念中顶点均取自V,边均取自E.如果在图G中点v是边e的一个端点,则称顶点v与边e在图G中相关联;如果图上两点u,v被同一条边相连,则称u,v在图G中相邻;若图G中两条边有至少一个公共端点,则称这两条边在图G相邻;端点重合为一点的边称为环;端点不相同的边称为连杆;设u和v是图G的顶点,图G中连接u和v的两条或两条以上的边称为图G中u,v间的重边或平行边;既无环边也无重边的图称为简单图;|V|和|E|都是有限的图称为有限图(finite graph).本文只考虑有限无向简单图.用图表示互连网络时,顶点代表网络节点(处理器),边代表节点之间直接的通信连接.

定义2.2[1-2]设G是一个无向图,G中一个点边连续交替出现的序列ω=v0e1v1e2···vkek称为图G的一条途径,其中v0和vk分别称为途径ω的起点和终点,ω上其余顶点称为中途点;图G中边不重复出现的途径称为迹;顶点不重复出现的迹称为路,起点和终点相同的途径称为闭途径,边不重复出现的闭途径称为闭迹,中途点不重复出现的闭迹称为圈;经过图G的每个顶点一次的圈称为一个Hamilton圈,记为H.

定义2.3[1-2]若一个图具有这样的一个图形,它的边仅在端点处相交,则该图称为平面图.设x和y是G中的两顶点,如果G中存在xy路,那么称x和y在G中是连通的.若一个图中任意两个顶点之间都有一条Hamilton 路,则称这个图为Hamilton连通图.

定义2.4[1-2]设G1=(V1,E1)和G2=(V2,E2)是两个无向图.G1和G2的笛卡尔乘积(Cartesian product)是无向图,记为G1×G2,其中V(G1×G2)=V1×V2={(v1,v2)|v1∈V1且v2∈V2},两个不同的顶点(x1,x2) 和(y1,y2)(其中x1,y1∈V(G1),x2,y2∈V(G2))相邻当且仅当或者x1=y1且x2y2∈E(G2),或者x2=y2且x1y1∈E(G1).

定义2.5[4]设G是n阶图,如果G中存在任意长为l(3≤l ≤n)的圈,则G称为泛圈的;如果在G中,对于任意一个顶点v,存在任意长为l(3≤l ≤n)的包含v的圈,则G称为点泛圈的;如果在G中,对于任意一条边e,存在任意长为l(3≤l ≤n)的包含e的圈,则G称为边泛圈的.在一个n阶二部图G中,如果G中存在任意长为偶数l(4≤l ≤n)的圈,则G称为偶泛圈的;如果在G中,对于任意一个顶点v,存在任意长为偶数l(4≤l ≤n)的包含v的圈,则G称为点偶泛圈的;如果在G中,对于任意一条边e,存在任意长为偶数l(4≤l ≤n)的包含e的圈,则G称为边偶泛圈的.

定义2.6[5]将十二面体连通圈网络中的每个顶点用一个三角形(3长的圈C3)来代替,且三角形的每个顶点仅位于十二面体中与该顶点关联的一条边上,得到的新网络称为1次十二面体-师连通圈网络,记为DSCC(1);再将1次十二面体-师连通圈网络DSCC(1)中的每个顶点用一个三角形来代替,且三角形的每个顶点仅位于DSCC(1)中与该顶点关联的一条边上,得到的新网络称为2次十二面体-师连通圈网络,记为DSCC(2);重复代替k次,得到的新网络称为k次十二面体-师连通圈网络,记为DSCC(k).

定义2.7[6]将k次十二面体-师连通圈网络DSCC(k)与K2的笛卡尔乘积定义为无向图,生成是新网络称为笛卡尔乘积网络DSCC(k)×K2.

引理2.1[6]DSCC(0)×K2是偶泛圈的.

引理2.2[6]DSCC(k)×K2是偶泛圈的.

§3 主要结果

通过引理2.1和2.2的结果,提出一个更一般性的结论,对于任意Hamilton平面连通图,它与K2的笛卡尔乘积图都有引理2.2的结果成立.结论的具体内容及其证明以定理的形式给出如下：

定理3.1任何一个Hamilton平面连通图G与K2的笛卡尔乘积G×K2都是偶泛圈的.

证设G=(V(G),E(G))是一个n阶的Hamilton平面连通图,其中

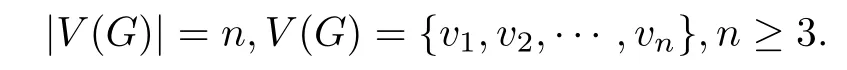
设G的一个Hamilton圈HG=v1v2···vi···vj···vnv1,其中1≤i,j ≤n.作出G×K2如图3.1所示,图中是HG的一个复制,HG和之间的边是序号相同的对应顶点之间的匹配,|V(G×K2)|=2n.在圈HG和中不相邻顶点之间的边未画出,因为这些边在G×K2中不影响它的偶泛圈性.

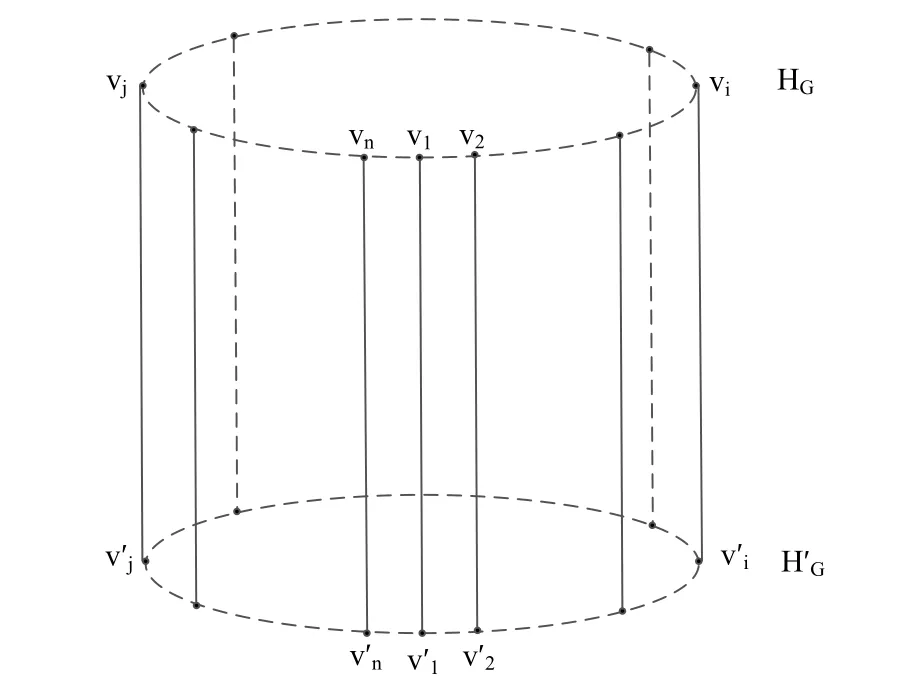
图3.1 DSCC(k)×K2

根据偶泛圈性的定义,只需证明G×K2中存在任意偶数长度l(4≤l ≤2n) 的圈即可.选择以边作为起始边,不妨假设i=1,以为起始边,向右依次找长为l的偶圈.在G×K2中观察到,圈长l是顶点序数i的两倍,利用在HG和中的序数i同时逐次递增的方式,找到包含边的所有偶数长度l(4≤l ≤2n)的圈如下.

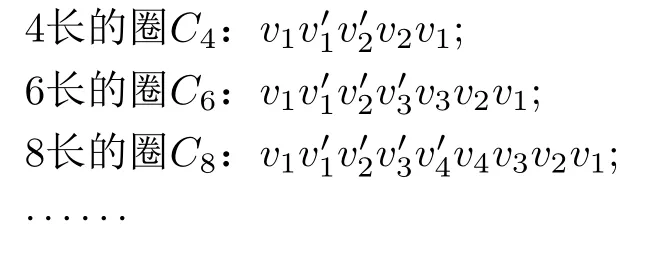
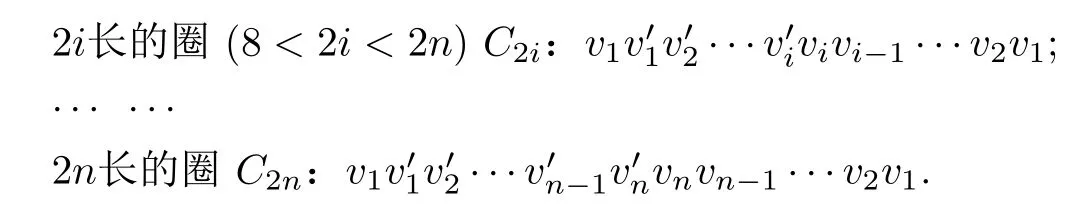
因此G×K2中存在长为4到2n的所有偶圈,故笛卡尔乘积G×K2是偶泛圈的.

下面讨论DSCC(k)×K2的泛圈性.当k ≥1时,DSCC(k)×K2的泛圈性如下.

定理3.2DSCC(k)×K2(k ≥1)是泛圈的.

证由泛圈性的定义知,只需证明DSCC(k)× K2(k ≥1)中存在任意长为l(3≤l ≤40×3k)的圈.根据圈长l的奇偶性,分为两种情形来讨论这些圈的存在性.

情形1 当l是偶数时,记m=l.

证明DSCC(k)×K2(k ≥1)中存在任意长为偶数m(3≤m ≤40×3k,m=4,6,···,40×3k)的偶圈,即证DSCC(k)×K2是偶泛圈的.根据定理3.1的结果,由于DSCC(k)是Hamilton平面连通图,所以DSCC(k)×K2是偶泛圈的.所以当l是偶数m时,所有m长的偶圈都是存在的.

情形2 当l是奇数时,记n=l.

证明DSCC(k)×K2(k ≥1)中存在任意长为奇数n(3≤n ≤40×3k,n=3,5,···,40×3k-1)的奇圈.当n=3时,因为DSCC(k)是由DSCC(k-1)中的每一个顶点被一个三角形代替得到的,所以DSCC(k)×K2中显然存在3 长的圈C3.

当n ＞3时,接着证明DSCC(k)×K2中存在任意长为n(5≤n ≤40×3k -1)的所有奇圈Cn.在情形1中,证明了DSCC(k)×K2中存在长为偶数m(4≤m ≤40×3k -2)的所有偶圈.现在任取其中的一个偶圈,记为Cm,通过偶圈Cm来构造出奇圈Cn=Cm+1.首先,显然DSCC(k)×K2中的每个顶点都是某一个三角形的顶点,故在找到m长的偶圈Cm中,它的每个顶点也是属于某一个三角形的.

其次,在构造偶圈Cm的过程中,在满足其条件的情况下,总能使得找到的圈Cm中存在至少一个这样的情况,那就是Cm(m为偶数)当且仅当包含某一个三角形中的两个顶点.假设这个三角形的顶点分别是vi1,vi2和vi3,包含在Cm中的顶点是vi1和vi2.此时把第三个顶点嵌入到偶圈Cm中,就能得到奇圈Cm+1,如图3.2所示.由m的任意性可知,在DSCC(k)×K2中能由偶圈Cm(4≤m ≤40×3k -2)构造出长为奇数n=m+1 (5≤n ≤40×3k -1)的所有奇圈.故当l是奇数n时,所有n长的奇圈都是存在的.

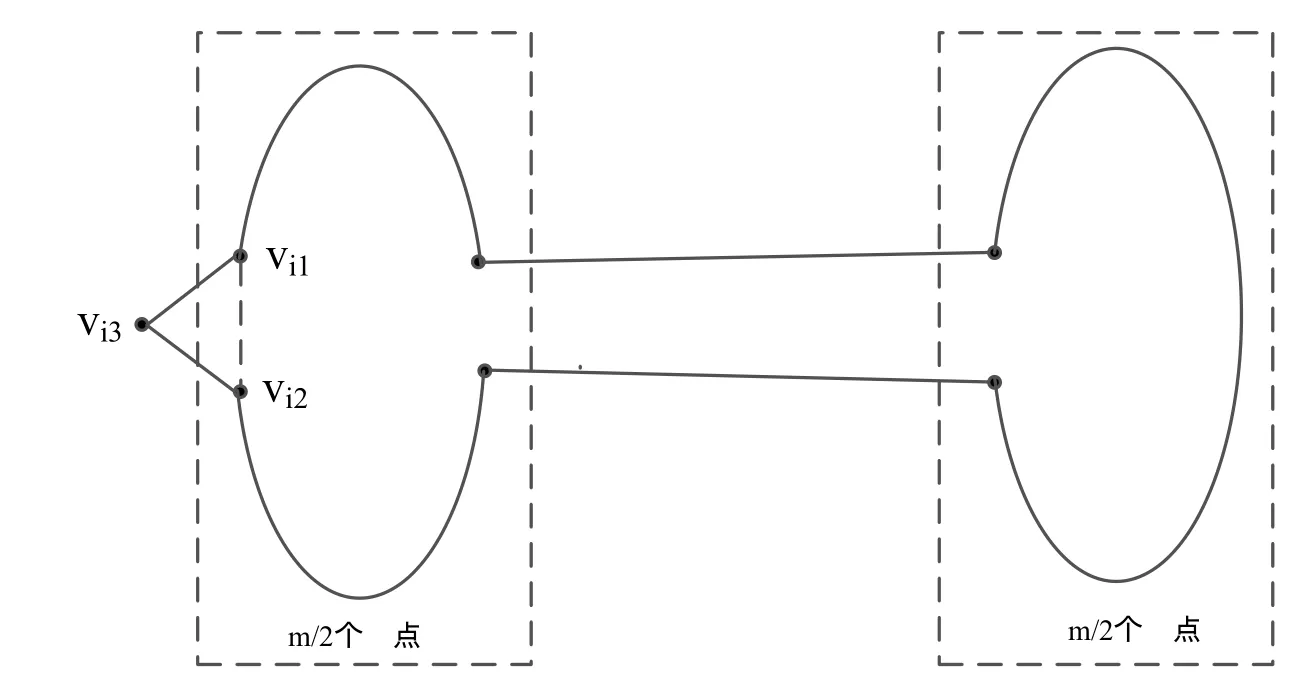
图3.2 Cm+1

综合以上所有情形,知道DSCC(k)×K2(k ≥1)中存在任意长为l(3≤l ≤40×3k) 的圈,即DSCC(k)×K2(k ≥1)是泛圈的.