关于G连通子集

平 征

(宁德师范学院数理学院,福建宁德 352100)

§1 引言

连通性是一类重要的拓扑性质,在拓扑学,分析学,几何学及相关的物理学,计算机科学等学科中发挥了积极的作用.作为连通性的拓展,A.Fedeli和A.Le Donne[1]定义了拓扑空间的序列连通性.H.C¸akallı等[2-3]引入并研究了满足第一可数公理的Hausdorff拓扑群中的G连通性,并将序列连通性归结为在通常收敛方法下的G连通性.林寿和刘丽[4]定义了一般集上的G方法及G收敛性,建立了较之于拓扑空间中通常收敛性更为一般的收敛概念;随后刘丽[5-7]研究了由G开集等确定的特殊集的性质和G序列紧空间;而后吴永兴和林福财[8]讨论了拓扑群的G连通相关性质和G拓扑;接着平征[9]借助G方法,引入G隔离集,讨论了一般集上的G连通性;近期刘丽和平征[10]引入了积集的G方法并讨论了积集的G连通性.

在研究过程中发现了文[2]的定义1给出的G序列连通子集的定义有一些瑕疵,导致在此基础上给出的四个等价条件并不成立.本文纠正了文[2]的定义1,给出了G序列连通子集的正确定义,并进一步验证该定义与文[9]中的G连通子集的定义是一致的.文[4]中介绍了X的子集Y上的子方法G|Y,本文在此基础上引入G|Y隔离集并定义了G|Y连通子集,讨论了G|Y连通子集与G连通子集的关系.

§2 预备知识

设X是一个集,记s(X)是X中的所有序列组成的集,s(X)的元写为x={xn}n∈N.设映射f:X →Y,记f(x)={f(xn)}n∈N.若X是一个拓扑空间,记c(X)是X中的所有收敛序列所组成的集,集X上的一种方法(简称为G方法)是一个函数G:cG(X)→X,其中cG(X)⊂s(X).序列x∈s(X)称为G收敛于l ∈X,若x∈cG(X)且G(x)=l.方法G:cG(X)→X称为正则的[4],若c(X)⊂cG(X)且对任何x∈cG(X)有G(x)=lim x.方法G:cG(X)→X称为子序列的[4],若x∈cG(X)且G(x)=l,且存在x 的子序列x′ ∈c(X)有lim x′=l.

定义2.1[4]设X是一个集,G是集X上的一个方法且A ⊂X.

(1)A称为X的G闭集,若x∈s(A)∩cG(X),则G(x)∈A.

(2)A称为X的G开集,若X A是G闭集.

(3) 集∩{F:F是X的G闭集,且A ⊂F}称为A的G闭包,记为.

对于集合X上的一个G方法及X上的任一子集A,A的G闭包是X的G闭集.

定义2.2[2]设X是一个集,G是集X上的一个方法且A ⊂X.A的子集F称为A中的G闭集,若存在X的G闭集U使得F=U ∩A.V称为A中的G开集,若AV是A中的G闭集.

引理2.3[11]设C是拓扑空间X的连通子空间.如果X中有一对隔离子集X1和X2使得C ⊂X1∪X2,则有C ⊂X1或C ⊂X2.

定义2.4[9]设G是集X上的一个方法,若X的子集A,B满足,则称A,B是G隔离的.

定义2.5[9]设G是集X上的一个方法,Y ⊂X,若Y不能表示为X的一对非空G隔离集之并,则子集Y称为G连通的.

定义2.6[4]设G是X上的一个方法,Y ⊂X.令cG|Y(Y)={x∈s(Y)∩cG(X):G(x)∈Y},G|Y:cG|Y(Y)→Y且G|Y(x)=G(x),x∈cG|Y(Y).则G|Y是X的子集Y上的子方法.

引理2.7[4]设G是X上的一个方法,A ⊂Y ⊂X,则

本文未定义的术语和符号,请参照文献[11].

§3 G序列连通子集

文[2]定义1给出了G序列连通性的下述定义.

设G是集X上的一个方法,A ⊂X,A称为G序列连通的,若不存在不交G闭子集U和V使得A ⊂U ∪V,且A ∩U和A ∩V是非空的.特别地,X称为G序列连通的,若不存在非空,不交G闭子集U和V使得X=U ∪V.

在此基础上,文[2]在引理1给出了G序列连通性的4个等价条件.

引理3.1[2]设G是集X上的一个方法,A ⊂X,下述条件等价：(i)A是G序列连通的;(ii)A不能表示成A中非空,不交G闭子集之并;(iii)A不能表示成A中非空,不交G开子集之并;(iv)不存在A中G开且G闭的真子集.

关于上述引理,给出下述例子.

例3.2设X=[0,2]赋予通常拓扑,G为通常收敛,G闭集即为闭集.取A=[0,1)∪(1,2]⊂X.下证A是G序列连通的.假设A不是G序列连通的,则存在不交闭集U,V使得A ⊂U ∪V,且∅,∅.因为[0,1),(1,2]分别是连通的,由引理2.3不妨设[0,1)⊂U,(1,2]⊂V.因为U,V为闭,所以1∈U ∩V.这与U,V不交相矛盾,因此A是G序列连通的.但是A=[0,1)∪(1,2],其中[0,1)=[0,1]∩A,(1,2]=[1,2]∩A分别是A中闭集,即A能表示为A中非空,不交闭集之并,所以A不满足引理2.1的(ii).

正是由于上述G序列连通子集定义不恰当,导致引理3.1中的条件(i)与(ii)并不等价.

本文将文[2]关于G序列连通的定义修订为下述定义3.3,并在此基础上修改引理3.1为下述引理3.4.

定义3.3设G是集X上的一个方法,Y ⊂X,Y称为G序列连通的,若Y不能表示成Y中非空,不交的G闭子集之并.

引理3.4设G是集X上的一个方法,Y ⊂X,下述条件等价.

(1)Y是G序列连通的;

(2)Y不能表示成Y中非空,不交G开子集之并;

(3) 不存在Y中非空G开且G闭的真子集.

证(1)⇒(2).假设Y能表示成Y中非空,不交G开集之并,即Y=U∪V,U和V均为Y中G开集,U ∩V=∅.由于U和V均为Y中G开集,得Y U=V和Y V=U分别是Y中G闭集,即Y能表示成Y中非空,不交G闭子集之并,即Y不是G序列连通的.矛盾,从而(1)⇒(2).

(2)⇒(3).假设存在Y中非空G开且G闭的真子集U,则Y U也是Y中非空G开且G闭的真子集.Y=U ∪(Y U),且U ∩(Y U)=∅,即Y能表示成Y中非空,不交G开子集之并.矛盾,从而(2)⇒(3).

(3)⇒(1).假设Y不是G序列连通的,则Y能表示成Y中非空,不交G闭子集之并,即Y=U ∪V,U和V均为Y中G闭集,U ∩V=∅.由于U为Y中G闭集,可知V=Y U为Y中G开集,因此V为Y中非空G开且G闭的真子集.矛盾,从而(3)⇒(1).

通过下面讨论可知上述所给出的G序列连通性实际上与定义2.5所给出的G连通性定义是一致的.

定理3.5设G是集X上的一个方法,Y ⊂X.Y是G序列连通与Y是G连通是一致的.

另一方面,假设Y不是G序列连通,则Y能够表示为Y中一对非空,不交G闭子集A,B之并,即Y=A ∪B,A=U ∩Y,B=V ∩Y,A ∩B=U ∩V ∩Y=∅,其中U,V分别是X中G闭.,同理.所以A,B为X上一对非空,不交G隔离集之并,因而Y不是G连通的.

综上可得Y是G序列连通的与Y是G连通是一致的.

§4 G|Y 连通子集

定义4.1设G是X上的一个方法,Y ⊂X,若Y不能表示为Y上一对非空G|Y隔离集之并,则子集Y称为G|Y连通的.

引理4.2设G是X上的一个方法,Y ⊂ X,A,B ⊂ Y.若A,B是X上一对G隔离集,则A,B是Y上一对G|Y隔离集.

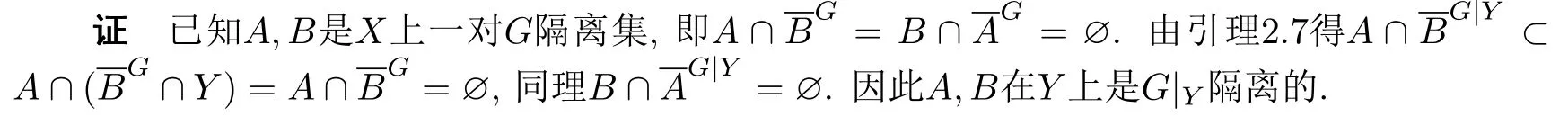
定理4.3设G是集X上的一个方法且Y ⊂X.若Y是G|Y连通,则Y是G连通.

证假设Y不是G连通的,则存在X上一对非空G隔离集A,B使得Y=A ∪B,由引理4.2得,A,B是Y上一对G|Y隔离集,因此Y不是G|Y连通的,矛盾.

定理4.3的逆命题不一定成立.

例4.4存在集X上的一个方法G及Y ⊂X满足

(1) 存在A,B是Y上G|Y隔离集,但不是X上G隔离集.

设X=[0,1],G是X上的一个方法,

(2)Y是G连通,但不是G|Y连通.

由(1)可知Y不是G|Y连通的.下面证明Y是G连通的.

设Y=[0,1)=A∪B,A∩B=∅,A,B非空.不妨设0,即0∈B,由A ⊂(0,1)知进而故Y不能表示为X中一对非空G隔离集之并,从而Y是G连通的.

致谢本文是在林寿教授的悉心指导下完成的,特此致谢！