一类双曲方程解的空间渐近性态

石金诚

(广州华商学院 数据科学学院,广东广州 511300)

§1 引言

1856年,Saint-Venant提出了一个著名的在数学和力学上具有广泛应用的原理,称之为Saint-Venant原则.随后Saint-Venant原则成为数学与力学领域最流行的研究内容之一.有关Saint-Venant原则的详细介绍可见文献[1-3].Saint-Venant型定理的一个共同特点是建立解的能量的指数衰减估计,当空间变量由近端向无穷远端移动时,其解的能量呈指数衰减.为了得到Saint-Venant型的解的空间指数衰减,人们总是假设解在无穷远处必须满足一些限制条件,可是,这样的假设在实际应用中并不一定成立,为此,许多学者转向研究Phragm´en-Lindelöf二择一结果.经典的Phragm´en-Lindelöf二择一定理指出: 调和方程的解从圆柱面有限的一端到无穷远处必随距离增长而呈指数增长或指数衰减.在研究Phragm´en-Lindelöf二择一定理时,不需要对解在无穷远处加任何限制条件.Payne等[4]给出了双调和方程在三个不同区域的Phragm´en-Lindelöf二择一结果.对于解的Saint-Venant原则或Phragm´en-Lindelöf 二择一研究目前也取得了一些成果(见[5-9]).已有的文献主要研究椭圆与抛物方程解的空间性态,对双曲方程研究较少.最近,一些新的文献开始研究双曲方程解的时间性态(见[10-13]).

解的“爆破”或“不存在”是偏微分方程一个重要的研究方向,在文献[14-17]中有详细的介绍,但大多数是关于椭圆或抛物方程的爆破研究.他们均是采用能量方法去研究解的爆破现象,得到一些解的爆破结果.特别的,在文献[17]中,Quintalina研究了一类非线性抛物方程解的空间性态,在给定的限制条件下,得到了一个类似于Phragm´en-Lindelöf二择一的结果,该结果表明,解或者在有限空间内爆破,或者解随着空间变量的增长而衰减.受文献[17]的启发,尝试研究双曲方程的解的空间衰减估计与爆破,得到解的类似于Phragm´en-Lindelöf二择一的结果: 解沿着空间趋于无穷远的过程中要么不整体存在,要么整体存在且沿着空间变量的增长而指数衰减.特别指出,国内也有一些学者开始进行解的空间衰减估计或Phragm´en-Lindelöf二择一的研究,文献[18-24]得到一些抛物方程解的空间性质.本文主要研究双曲型方程

的经典解,其中q2=u,iu,i,ρ是一个函数并且γ是一个大于零的常数.考虑半无限带形区域上方程(1)的一个初边值问题,初始条件为

其中R={(x1,x2)|0＜x2＜h,x1＞0}.边界条件为

假设满足(1)的经典解是存在的.其中函数g满足边界条件g(0,t)=g(h,t)=0.为了方便起见,引入符号

对函数ρ,假设存在一个大于零的常数ρM满足

本文讨论了解关于空间的性态,得到一个类似于Phragm´en-Lindelöf二择一的结果.对于解的爆破现象的研究,现有文献主要集中在解的时间爆破,除文献[17] 外,尚未发现有文献研究解的空间爆破.相对于文献[17],由于考虑对象由抛物方程变为双曲方程,如何构造能量函数是本文的关键.如何推导出能量函数所满足的微分不等式以及巧妙求解的方法,是本文最大的特色.本文所得的解的点点估计结果是双曲方程所特有的.

本文采取以下符号约定,˙u表示对u关于时间t求导数.用逗号表示求偏导,用,i表示对xi求偏导数(i=1,2),如:u,i表示.重复指标表示求和,如

§2 解的空间爆破或衰减

在下文中将使用如下引理.

引理2.1[16]对于光滑函数u(ξ),当u(0)=u(h)=0时,Poincar´e不等式

成立.而对于光滑函数u(ξ),当u(0)=0或u(h)=0时,Poincar´e不等式

成立,其中π是大于零的常数.

引理2.2定义函数

证首先考虑

因此可得

定义函数W满足

当q2=0时,W=0.联合(12) 与(13)即可得到(10)的结果.

定理2.1设u是方程(1)满足初边值条件(2)-(4)的解,当空间变量z趋于无穷时,解的能量表达式或者满足

该不等式表明解在有限空间内爆破.或者解的能量表达式满足估计

该不等式表明解的能量按照幂函数衰减,(14)式的结果与(15)式的结果有且只有一个成立.其中M6(t) 是一正函数.

证(10)式两边同时对z求偏导,可得

如果假设˙uf满足

其中α是任意大于1的常数.由(10)式可知

其中

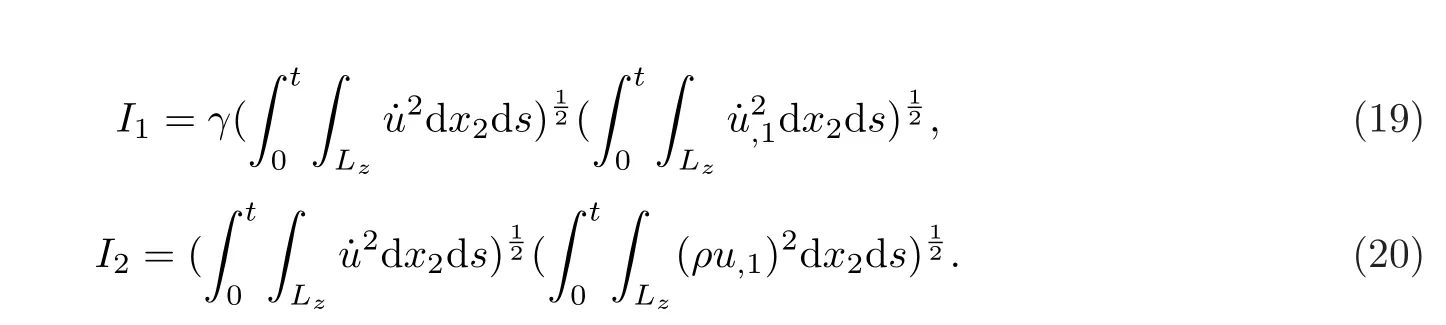
由Hölder不等式和(19)式,可得

由Young不等式和(22)式,可得

其中M4(t)=M1(t).将(8)代入(25)式,可得

下面分两种情形来讨论.

情形1若假设存在一个z0＞0,使得G(z0,t)＜0,那么对于所有的z ≥z0,有G(z,t)＜0.因此得出结论

对(29)式从0到z积分,可得

不等式(30)表明,当z →∞时,-G(z,t)＜0,显然与假设矛盾.故解在z为有限值时不存在.

情形2另一方面,如果假设G(z,t)≥0对于所有的z ≥0,得到

它描述了当z ≥0时,解是沿着空间z →∞时按照幂函数衰减.结合以上两种情况,证明了定理2.1的结果.

§3 解的指数衰减估计

在定理2.1情形2的条件下,当G(z,t)≥0时,建立了解的渐近衰减估计.下面证明该衰减至少是指数衰减.

定理3.1设u是方程(1)满足初边值条件(2)-(4)的解,且假设(9)式中定义的函数G(z,t)≥0,则解的能量表达式满足空间衰减估计

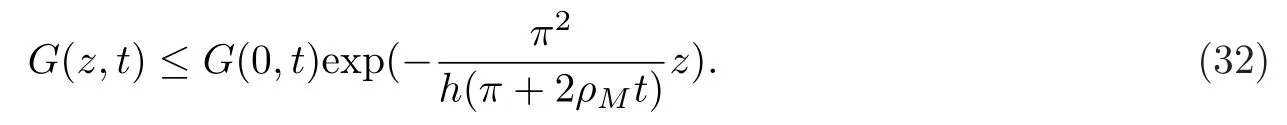
如果定义一个新的能量函数

则对于所有的z ≥0满足估计

由Hölder不等式及(7)和(9)式,可得

(37)式可变形为

求解(38)式可得

(39)式表明(15)式中的渐近衰减可以达到指数衰减,(32)式的结果得证.显然

成立.(39)式,由L’Hospital法则可得

联合(40)和(41)式可得

联合(7),(33)和(41)式,由Cauchy-Schwarz不等式,可得

由(42)可得

联合(40)和(43)式可得

§4 解的点点衰减估计

在定理2.1情形2的条件下,还可以得到u2(z,x2,t)的渐近性态.

定理4.1在情形2的假设下,则

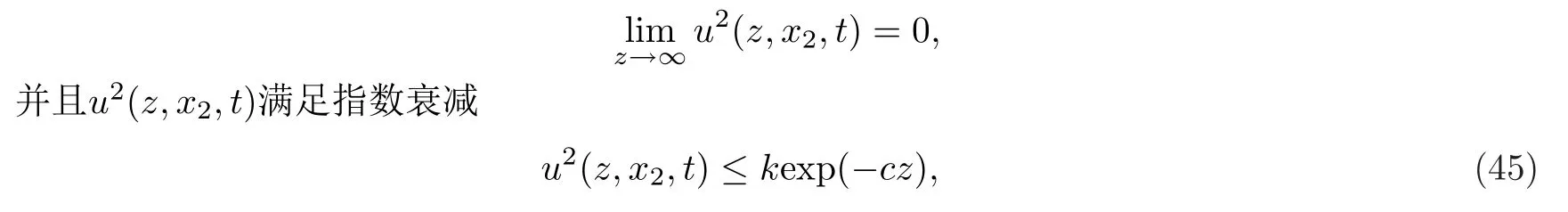
其中k和c均是大于零的常数.

证在情形2中,可知

由Hölder不等式,可得

由(3)式可知

联合(8)和(49)式可得

对(32)式应用L’Hospital法则得: 当z →∞时

联合(50)和(51)式可得

下一步证明当z →∞时

由(3)式可知

由上式有

联合(34),(52)和(53)式可得

结合(48),(52)和(54)式可得

所以证明了定理4.1的第一部分.定义一个新的函数

采用类似于(48)-(55)式的过程,可得

其中k是一个大于零的常数.所以定理4.1得证.