有限正交空间中格的秩生成函数和特征多项式

李 艳 ,赵燕冰 ,霍元极

(1.张家口学院 数学与信息科学学院,河北张家口 075000;2.张家口职业技术学院 基础部,河北张家口 075000;3.河北北方学院理学院,河北张家口 075000)

§1 引言

在偏序集和格中的秩生成函数和特征多项式有许多文献都做了介绍和研究[1-3],文献[4]对一致偏序集作了进一步的研究.有限域上的典型群几何有着广泛的应用,如文献[5]研究了伪辛空间中全迷向子空间的Critical问题,文献[6-9]研究了在有限典型群作用下,由子空间轨道生成格的秩函数和特征多项式,并给出了相应的定义和表示式.本文讨论有限典型群的正交群O2ν+δ,Δ(Fn)作用奇特征正交空间下,子空间轨道生成格的秩生成函数和特征多项式.本文沿用文献[1,9]中的名词术语,并引用[1-2]和[9-10]中的一些结果.

设Fq是q个元素的有限域,q是一个素数幂.是Fq上2ν+δ维行向量空间,其中ν是非负整数,δ=0,1或2,charFq2,用[M1,M2,···,Ml]表示对角矩阵,其主对角线上依次是方阵.令上满足TS2ν+δ,Δ tT=S2ν+δ,Δ的所有(2ν+δ)×(2ν+δ)的矩阵T,对矩阵的乘法作成一个群,称为Fq上关于S2ν+δ,Δ的2ν+δ级正交群,记作O2ν+δ,Δ(Fq).它在上作用如下

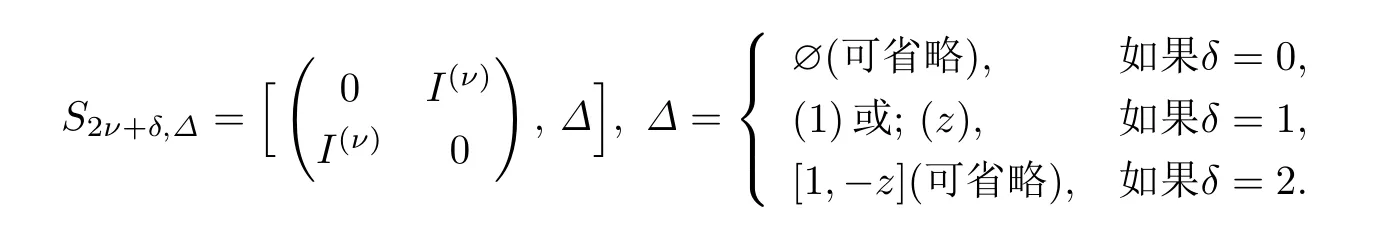
众所周知PS2ν+δ,Δ tP合同于标准形[10]

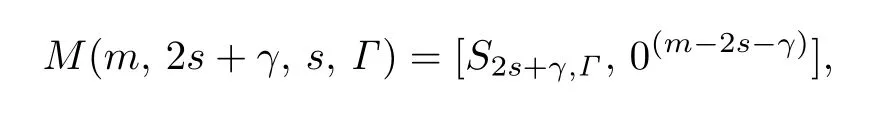
其中0≤s ≤[(m-γ)/2],Γ=0,1或2,并且

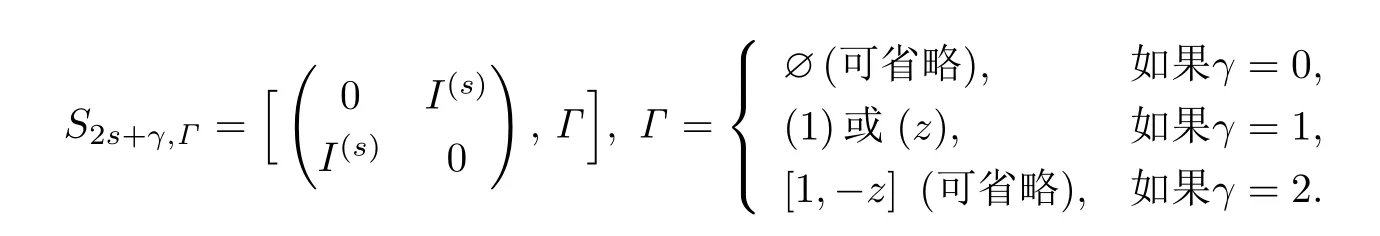
称P是中关于S2ν+δ,Δ的(m,2s+γ,s,Γ)型子空间,简称(m,2s+γ,s,Γ)型子空间.

§2 预备知识

首先回顾文献[9-10]中关于奇特征有限几何理论的一些基本知识.

引理2.1(见[9,p60]) 在中,关于S2ν+δ,Δ存在(m,2s+γ,s,Γ)型子空间当且仅当

用M=M(m,2s+γ,s,Γ;2ν+δ,Δ)表示中关于S2ν+δ,Δ的全体(m,2s+γ,s,Γ)型子空间的集合.当δ=0或2时,分别写成M(m,2s+γ,s,Γ;2ν)或M(m,2s+γ,s,Γ;2ν+2).M是中的子空间集在正交群O2ν+δ,Δ(Fq)作用下的一条轨道[9-10].

令L(M)=L(m,2s+γ,s,Γ;2ν+δ,Δ)是M中子空间非空交组成的集,约定是M中0个子空间的交.如果按子空间的反包含关系,规定L(m,2s+γ,s,Γ;2ν+δ,Δ)的偏序≥,即对于的子空间U,W,有.那么L(m,2s+γ,s,Γ;2ν+δ,Δ)作成有限格,称为由M(m,2s+γ,s,Γ;2ν+δ,Δ)生成的格,记为LR(m,2s+γ,s,Γ;2ν+δ,Δ).由[9]中定理5.12,如果

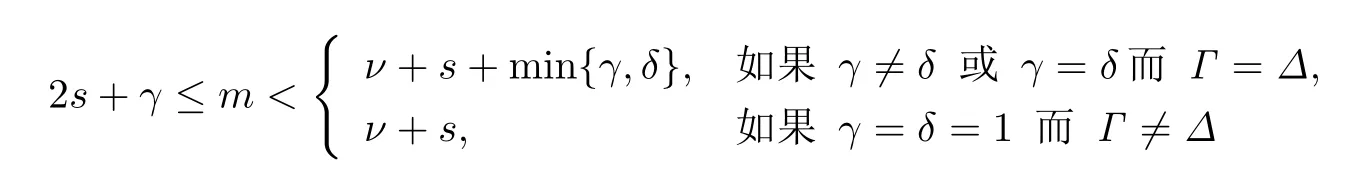
成立,那么LR(m,2s+γ,s,Γ;2ν+δ,Δ)由和满足

的所有(m1,2s1+γ1,s1,Γ1)型子空间组成.如果

成立,那么LR(m,2s+γ,s,Γ;2ν+δ,Δ)由和满足(2)而不列入文献[9]中表5.5中的所有(m1,2s1+γ1,s1,Γ1)型子空间组成.

定义2.1[9]设P是有0的偏序集,N0是非负整数所成的集合.函数

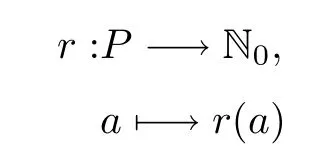
叫P上的秩函数,如果下面的(i)和(ii)成立.

(i)r(0)=0;

(ii) 对于a,b ∈P而ab[9],那么r(b)=r(a)+1.

若含有0的有限偏序集P中,P的所有极大链都具有相同的长度n,则称P的秩为n,记为r(P)=n,并且称P为秩n的分次偏序集,如果此偏序集是格,就称它为秩n的分次格.

定义2.2[2]若P是秩n的分次偏序集,并且其中有pi个元素的秩为i,则称多项式

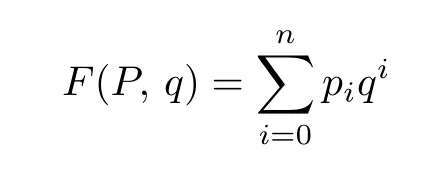
为P的秩生成函数.当P是一个格L时,F(P,q)就称为格L的秩生成函数.

引理2.2(见[9,p97]) 设n=2ν+δ ＞m ≥1,而(m,2s+γ,s,Γ)满足引理2.1中(1)式,对于

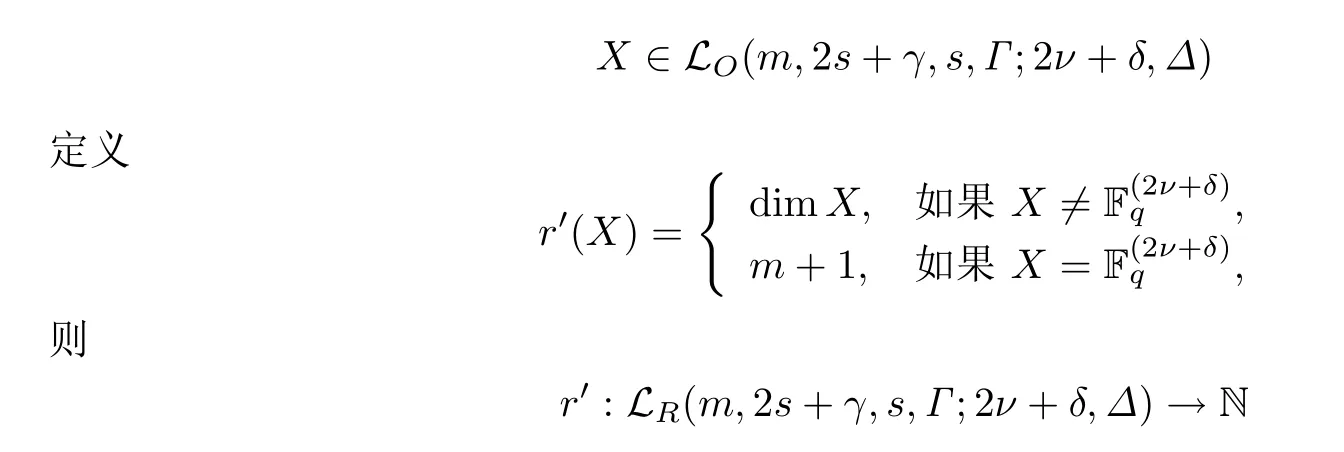
是格LR(m,2s+γ,s,Γ;2ν+δ,Δ)的秩函数.

定义2.3[9]设P是有最小元0和最大元1的有限偏序集,并且P上有秩函数r和Möbius函数μ,那么多项式

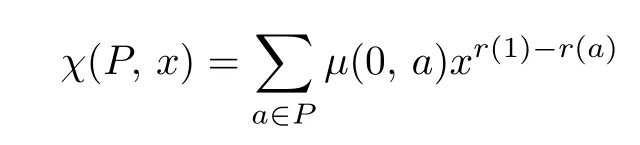
叫做P上的特征多项式.

§3 主要结果

关于格LR(m,2s+γ,s,Γ;2ν+δ,Δ)的秩生成函数,特征多项式有如下结果.为了表述上的方便,记

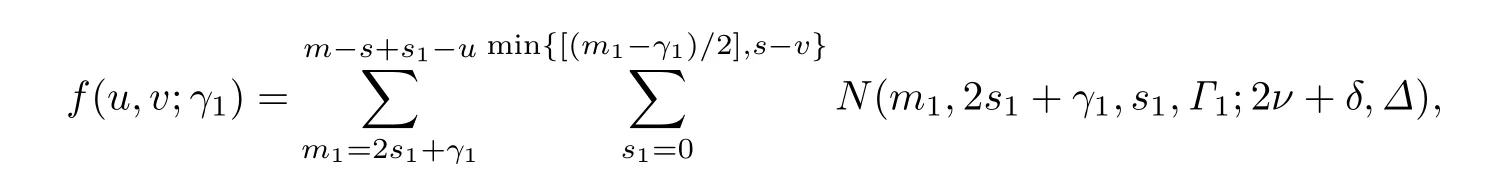
其中(m1,2s1+γ1,s1,Γ1)满足引理2.1中(1)和(2)而γ1=0,1或2,

定理3.1设1≤m1≤m ≤2ν+δ-1,子空间(m,2s+γ,s,Γ)与(m1,2s1+γ1,s1,Γ1)满足(1)式且(2)式成立

(i) 如果γ=0,那么LR(m,2s,s;2ν+δ,Δ)的秩生成函数是

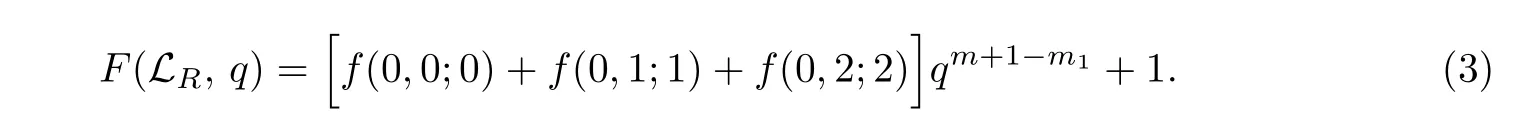
(ii) 如果γ=1,那么LR(m,2s+1,s,Γ;2ν+δ,Δ)的秩生成函数是

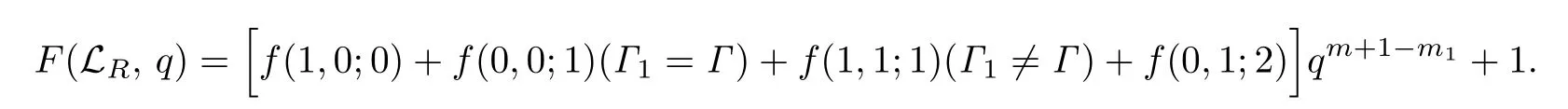
(iii) 如果γ=2,那么LR(m,2s+2,s,Γ;2ν+δ,Δ)的秩生成函数是

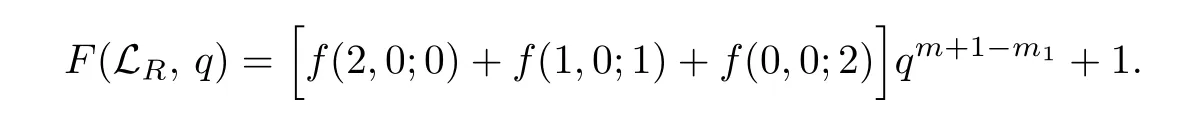
证由引理2.2知,对于X ∈LR(m,2s+γ,s,Γ;2ν+δ,Δ),定义

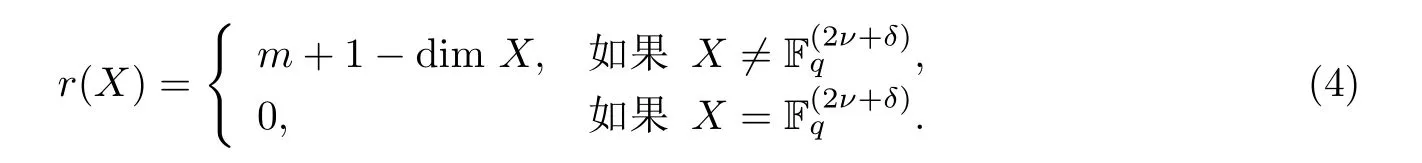
那么r:LR(m,2s+γ,s,Γ;2ν+δ,Δ)→N0是格LR(m,2s+γ,s,Γ;2ν+δ,Δ)的秩函数.

设P ∈LR(m,2s+γ,s,Γ;2ν+δ,Δ),考虑到LR(m,2s+γ,s,Γ;2ν+δ,Δ)中子空间的组成,如果,那么r(P)=0,所以LR(m,2s+γ,s,Γ;2ν+δ,Δ)中秩为0的子空间个数是1.由文献[9]中定理5.10可知

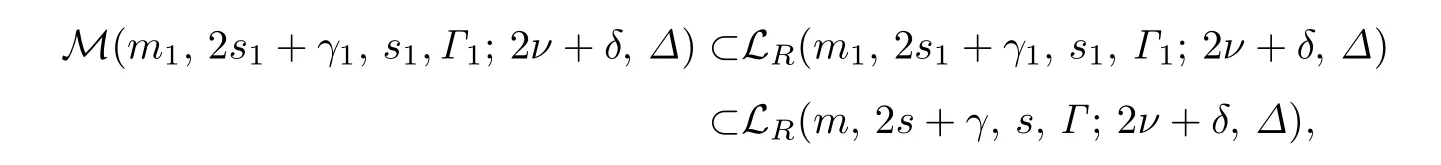
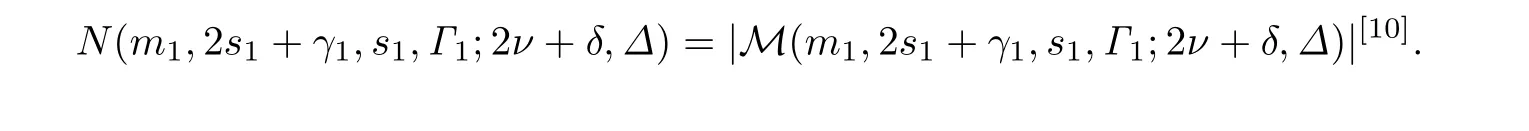
只证明情形(i),对于情形(ii),(iii)类似可证.下面分别对γ1=0,1或2进行计算.

a)γ1=0.这时(1) 式成为

(2)式变成

在m1取定后,s1满足0≤s1≤min{[m1/2],s}.所以当(m1,2s1+γ1,s1,Γ1)满足(1) 和(2)时,秩为i=m+1-m1的子空间P的个数是

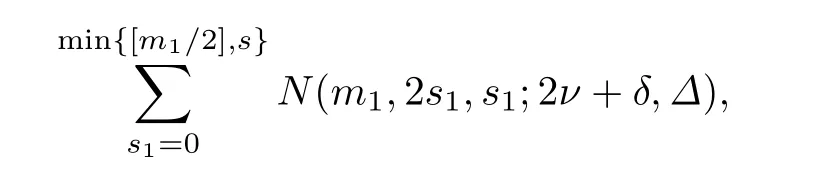
由(6)有0≤m1≤m-s+s1,所以m-s+s1≤ν+s1.由(5)和m1≤m-s+s1,可得2s1≤m1≤m-s+s1.因此当(m1,2s1,s1)满足(1)和(2)时,LR(m,2s+γ,s,Γ;2ν+δ,Δ)中F(2ν+δ)q的个数是

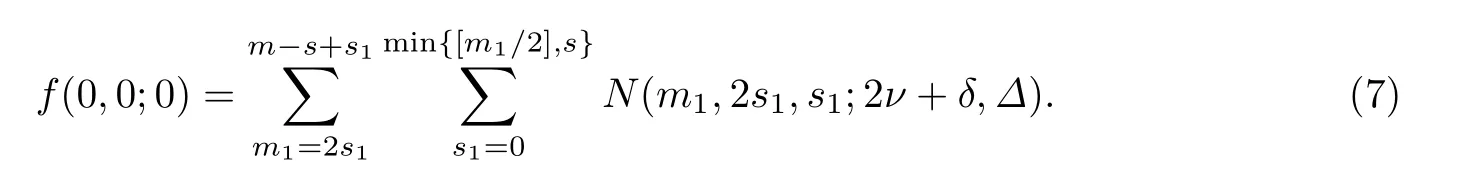
b)γ1=1.这时(1)式成为

(2)式变成

在m1取定后,s1满足0≤s1≤min{[(m1-1)/2],s -1},所以在(m1,2s1+1,s1,Γ1)满足(1)和(2)时,秩为i=m+1-m1的子空间P的个数是

由(9)有0≤m1≤m-s+s1,从(8)和m1≤m-s+s1,可得2s1+1≤m1≤m-s+s1.所以在(m1,2s1+1,s1,Γ1)满足(1)和(2)时,LR(m,2s+γ,s,Γ;2ν+δ,Δ)中的个数是

c)γ1=2.这时(1)式成为

(2)式变成

在m1取定后,s1满足0≤s1≤min{[(m1-2)/2],s-2},所以在(m1,2s1+2,s1)满足(1)和(2)时,秩为i=m+1-m1的子空间P的个数是

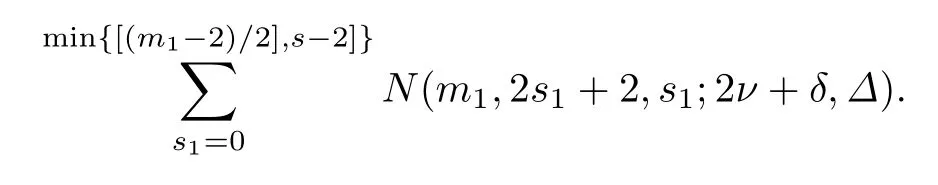
由(12)有0≤m1≤m-s+s1.从(11)和m1≤m-s+s1可得2s1+2≤m1≤m-s+s1.所以在(m1,2s1+2,s1)满足(1)和(2)时,LR(m,2s+γ,s,Γ;2ν+δ,Δ)中的个数是

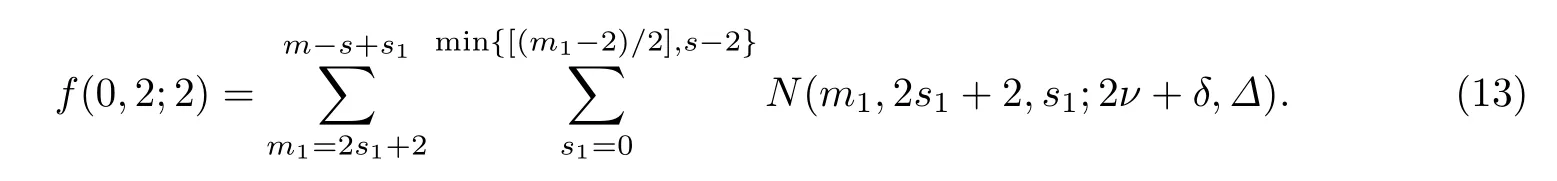
定理3.2设n=2ν+δ ＞m ≥1,并且(m,2s+γ,s,Γ)满足(1)式.

(i) 如果γ=0,那么特征多项式χ(LR(m,2s,s;2ν+δ,Δ),x)为

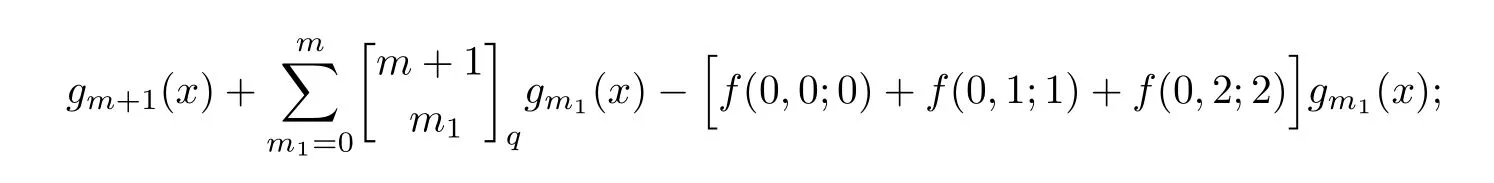
(ii) 如果γ=1,那么特征多项式χ(LR(m,2s,s;2ν+δ,Δ),x)为

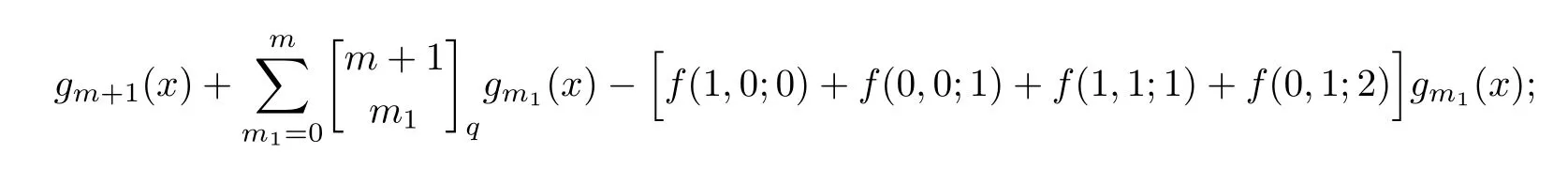
(iii) 如果γ=2,那么特征多项式χ(LR(m,2s,s;2ν+δ,Δ),x)为

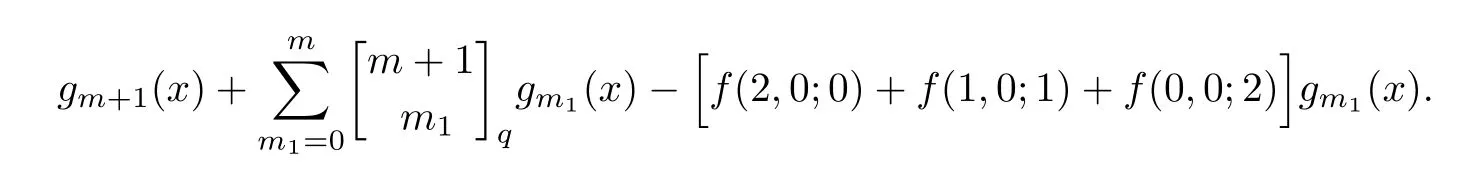
其中gm+1(x),gm1(x)为Gauss多项式[9],x为未知元.

证由(4)式及引理2.2,可知r是LR(m,2s+γ,s;2ν+δ,Δ)的秩函数.

和r(X)=m+1-dimX,,并且特征多项式χ(L1,x)=χ(LR(Fm+1),x),而L0的最大元和最小元分别是0和V0,L1的最大元和最小元分别是0和V1所以L0和L1的特征多项式分别是

对上述两个等式进行Möbius 反演,可得

取定满足(1)和(2)的(m1,2s1+γ1,s1,Γ1),那么由[10]中的定理6.26,可知

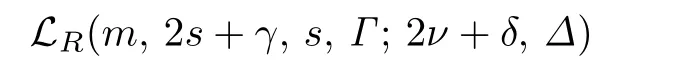
中(m1,2s1+γ1,s1,Γ1)型子空间的个数是N(m1,2s1+γ1,s1,Γ1;2ν+δ,Δ).因为L1{V1}中m1维子空间的个数是所以

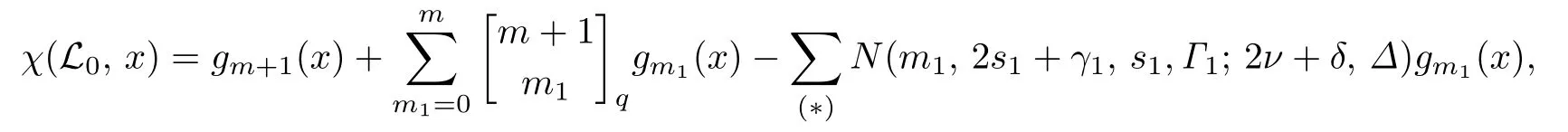
其中(*)表示(m1,2s1+γ1,s1,Γ1)满足(1)和(2).

在定理3.1的证明中,对γ=0,1,或2分别算出了满足(1)和(2)的LR(m,2s+γ,s,Γ;2ν+δ,Δ)中的个数及其表示式,将其代入上式可得定理3.2.

作为定理3.2的特殊情形,有如下结果.

推论3.3设n=2ν+δ ＞1,那么

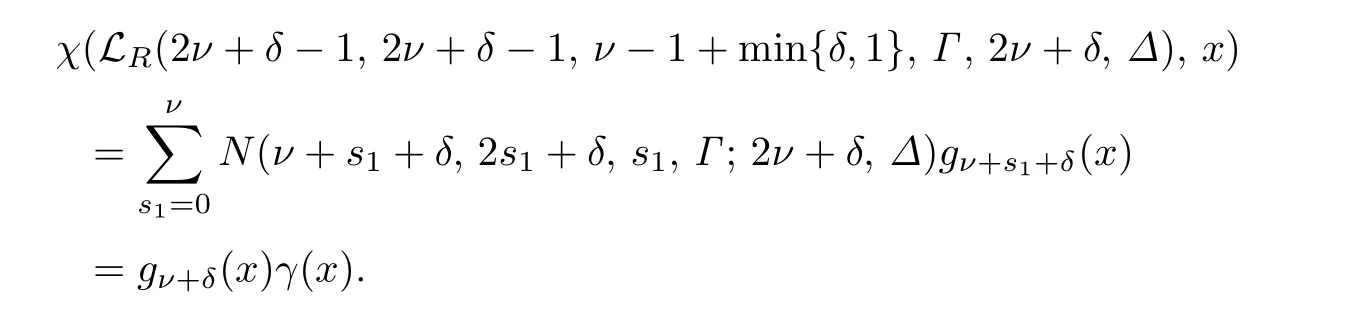
其中gν+s1+δ(x),gν+δ(x)为Gauss多项式,γ(x)∈Z[x]是首一多项式.

证类似于文献[9]中推论8.20的证明,可证推论3.3.