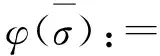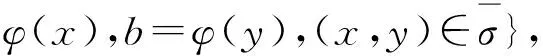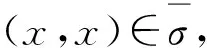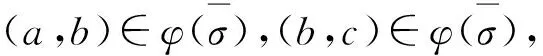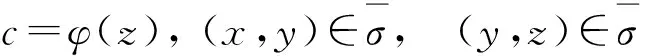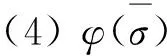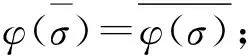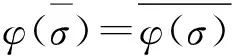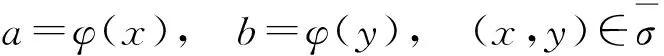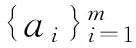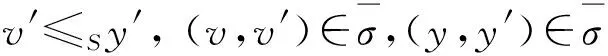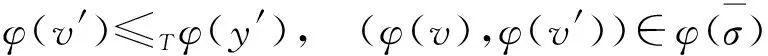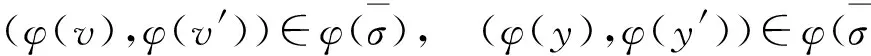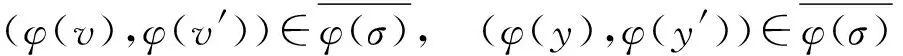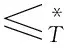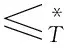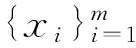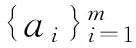可消偏序半群的可消偏序扩张与商序同态
邵海琴, 郭莉琴
(天水师范学院 数学与统计学院, 甘肃 天水 741001)
可消偏序半群的可消偏序扩张与商序同态
邵海琴, 郭莉琴
(天水师范学院 数学与统计学院, 甘肃 天水 741001)
引入偏序半群的商半拟序的概念,利用商半拟序给出了可消偏序半群上的偏序可扩张为可消偏序的充分条件.通过偏序半群的半拟序σ、模σ的闭半拟链,商半拟序和偏序扩张以及可消偏序半群的可消偏序扩张,对偏序半群的商序同态进行了刻画,得到了若干重要的结论.
可消偏序半群; 半拟序; 商半拟序; 闭半拟链; 偏序扩张; 可消偏序扩张; 商序同态
Journal of Zhejiang University(Science Edition), 2016,43(5):512-516,536
1 引言和预备知识
设(S,·,≤)是偏序半群[1].对∀a,b,c∈S,若S满足
ac≤bc⟹a≤b,ca≤cb⟹a≤b,
则称(S,·,≤)是可消的.S上的一个二元关系σ,若满足:(1)≤⊆σ;(2)若(a,b)∈σ,则对任意的c∈S,(ac,bc)∈σ,(ca,cb)∈σ,称σ为S上的半拟序[2]. 若S中的元素列(x,a1,b1,…,an,y)满足
x≤a1σb1≤…≤an-1σbn-1≤anσy,
则称其为S上模σ的半拟链[2], 若x=y, 则称该半拟链为闭的, 其中,n为该半拟链的长度,x,y分别为该半拟链的首项与尾项. 对于模σ的闭半拟链(x,a1,b1,…,an,x),若x=ai=bj(i=1,2,…,n;j=1,2,…,n-1), 则称此闭半拟链的长度为零.
设(S,·,≤S),(T,*,≤T)是偏序半群,φ:S→T是偏序同态[1].若对∀a,b∈S,∃x,y∈S,φ满足
φ(a)≤Tφ(b)⟹x≤Sy,φ(a)=φ(x),φ(b)=φ(y),
则称φ为S到T的商序同态[3].
设(S,·,≤)是偏序半群. 若≤*为S上的另一个偏序关系,且对∀a,b∈S,a≤b⟹a≤*b, 则称≤*为≤的偏序扩张[4]. 若S是可消偏序半群,≤*为≤的偏序扩张, 且≤*为S上的可消偏序,则称≤*为≤的可消偏序扩张[4].
偏序代数系统的偏序扩张一直受学者关注,文献[2,4-8]等对其进行了深入细致的研究.设(S,·,≤)是可换偏序幺半群,P1是S的正锥[4],若令P={x∈S|(∃a,b∈S)b≤a,xb=a}, 则P是S的偏序幺子半群,且P1⊆P. 文献[4]通过S包含P的子幺半群,讨论了可换偏序半群的偏序扩张与有限全序扩张问题,但其中给出的偏序扩张的方法只适用于可换偏序幺半群, 且在实际操作时难度较大. 为了解决这一问题,文献[2]引入了偏序半群的半拟序、半拟链, 通过半拟序、半拟链讨论了偏序半群的偏序扩张与有限全序扩张问题. 虽然文献[2]给出的偏序扩张方法适用于一般偏序半群和偏序半环[9],且较易操作,但仍无法解决可消偏序半群的可消偏序扩张问题. 为此,需引入偏序半群S上的商半拟序的概念.
定义1设(S,·,≤)是偏序半群,σ为S上的半拟序.对∀a,b∈S,∃x,y∈S,若σ满足
则称σ为S上的商半拟序.
商序同态是偏序半群中一个重要的研究课题,而偏序半群的一些重要概念在偏序半群各类问题特别是在与偏序同态和商序同态有关的问题的研究上具有举足轻重的作用[3,10-13].本文在文献[2]的基础上,给出了可消偏序半群上的偏序可扩张为可消偏序的一个充分条件,且通过偏序半群的半拟序σ、模σ的闭半拟链、商半拟序、偏序扩张以及可消偏序半群的可消偏序扩张,对偏序半群的商序同态进行了刻画.
本文还用到以下引理、定理、术语和符号.
引理1[13]设(S,·,≤)是偏序半群,σ为S上的半拟序. 若令
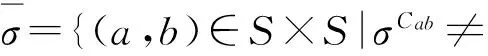
定理1[2]设(S,·,≤)是偏序半群,σ为S上的半拟序. 若S中任意模σ的闭半拟链的长度均为零, 则可将≤扩张为≤*, 使得(S,·,≤*)是偏序半群.
这里, 把定理1中的≤*称为≤关于σ的偏序扩张, 用σCxy表示S的所有以x为首项,y为尾项的模σ的半拟链集.
另外, 文中未加以说明的术语和符号均来自文献[1-2,4,11].
2 主要结果
定理2设(S,·,≤)是可消偏序半群,σ为S上的商半拟序. 若S中任意模σ的闭半拟链的长度均为零, 则可将≤扩张为≤*, 使得(S,·,≤*)是可消偏序半群.
证明定义S上的二元关系≤*如下:
对∀x,y∈S,有x≤*y⟺σCxy≠∅.
由定理1知,可将≤扩张为≤*, 使得(S,·,≤*)是偏序半群.下面只需证明≤*是可消的即可.
对任意的a,b,c∈S, 若ac≤*bc, 则σC(ac)(bc)≠∅, 于是由σ为S上的商半拟序知, ∃x,y∈S,有

ac≤a1σb1≤…≤an-1σbn-1≤anσx,
x≤c1σd1≤…≤cm-1σdm-1≤cmσac;
bc≤e1σf1≤…≤ep-1σfp-1≤epσy,
y≤g1σh1≤…≤gq-1σhq-1≤gqσbc.
从而有
ac≤a1σb1≤…≤an-1σbn-1≤anσx≤c1σd1≤…≤
cm-1σdm-1≤cmσac;
bc≤e1σf1≤…≤ep-1σfp-1≤epσy≤g1σh1≤…≤
gq-1σhq-1≤gqσbc.
由于S中任意模σ的闭半拟链的长度均为零,因此,
ac=ai=bj=cs=dt=x(i=1,2,…,n;j=1,2,…,
n-1;s=1,2,…,m;t=1,2,…,m-1);
bc=eu=fv=gw=hz=y(u=1,2,…,p;v=1,2,…,
p-1;w=1,2,…,q;z=1,2,…,q-1).于是,由x≤y得ac 引理2设(S,·,≤S),(T,*,≤T)是偏序半群,φ是S到T的商序满同态,σ为S上的半拟序, 若令 a=φ(x),b=φ(y), 于是∃xz,yz∈S,有 引理3设(S,·,≤S),(T,*,≤T)是偏序半群,φ是S到T的商序满同态,σ为S上的半拟序. 若令φ(σ):={(a,b)∈T×T|(∃x,y∈S)a=φ(x),b=φ(y),(x,y)∈σ}, 则 (2) 若σ是可消的, 则φ(σ)也是可消的; (3) 若σ是商半拟序, 则φ(σ)也是商半拟序; (4) 若S中任意模σ的闭半拟链的长度均为零, 则T中任意模φ(σ)的闭半拟链的长度也均为零. 证明(1)(i)≤T⊆φ(σ). 对∀a,b∈T, 若a≤Tb, 则∃x,y∈S,有 a=φ(x),b=φ(y),φ(x)≤Tφ(y), 由φ是商序同态,∃x1,y1∈S,有 x1≤Sy1,a=φ(x)=φ(x1),b=φ(y)=φ(y1). 于是有(x1,y1)∈σ, 从而有(φ(x1),φ(y1))∈φ(σ), 即(a,b)∈φ(σ), 因此≤T⊆φ(σ); (ii)φ(σ)对T的运算相容.对∀a,b∈T, 若(a,b)∈φ(σ), 则∃x,y∈S,有 a=φ(x),b=φ(y), (x,y)∈σ. 又对任意的c∈T, 由φ是满同态和σ的相容性得∃z∈S,有 c=φ(z),a*c=φ(xz), b*c=φ(yz), (xz,yz)∈σ,于是有(a*c,b*c)∈φ(σ); 同理可得,(c*a,c*b)∈φ(σ). 综上所述,φ(σ)是T上的半拟序. 由此得 a=φ(x),b=φ(y), (x,y)∈σ,(y,x)∈σ, a=φ(x),b=φ(y), (x,y)∈σ,(y,x)∈σ, (2)对∀a,b,c∈T,∃x,y,z∈S,若(a*c,b*c)∈φ(σ), 则 a=φ(x),b=φ(y),c=φ(z), (xz,yz)∈σ, 由σ是可消的,得(x,y)∈σ, 由此得(a,b)∈φ(σ), 即φ(σ)是右可消的; 同理可证φ(σ)是左可消的; a≤Ta1σb1≤T…≤Tam-1σbm-1≤Tam≤Tb. 对a,b,ai,bj(i=1,2,…,m;j=1,2,…,m-1),由φ是满同态知,存在x,y,xi,yj∈S(i=1,2,…,m;j=1,2,…,m-1),使得 a=φ(x),b=φ(y),ai=φ(xi),bj=φ(yj), i=1,2,…,m;j=1,2,…,m-1, 于是有 φ(x)≤Tφ(x1)φ(σ)φ(y1)≤T…≤T φ(xm-1)φ(σ)φ(ym-1)≤Tφ(xm)φ(σ)φ(y). 对φ(x)≤Tφ(x1),φ(yi)≤Tφ(xi+1)(i=1,2,…,m-1),∃v,ui,vj∈S,由φ是S到T的商序同态得 v≤Su1,vi≤Sui+1,i=1,2,…,m-1, φ(x)=φ(v),φ(xi)=φ(ui),φ(yj)=φ(vj), i=1,2,…,m;j=1,2,…,m-1. 对φ(xi)φ(σ)φ(yi),有φ(ui)φ(σ)φ(vi)(i=1,2,…,m-1);对φ(xm)φ(σ)φ(y),有φ(um)φ(σ)φ(y).由此得uiσvi(i=1,2,…,m-1),umσy. 于是由v≤Su1,uiσvi,vi≤Sui+1(i=1,2,…,m-1),umσy,得∃v′,有 v≤Su1σv1≤S…≤Sum-1σvm-1≤Sumσy, 即σCvy≠∅. 又因为σ为S上的商半拟序,∃v′,y′∈S,所以有 从而有 即∃φ(v′),φ(y′)∈T,使得 φ(v′)≤Tφ(y′), φ(v′)≤Tφ(y′), 由定义1知,φ(σ)是T上的商半拟序; (4) 设(a,a1,b1,…,am-1,bm-1,am,a)是T中任意模φ(σ)的闭半拟链,则有 a≤Ta1φ(σ)b1≤T…≤Tam-1φ(σ)bm-1≤Tamφ(σ)a. 对a,ai,bj,由φ是满同态知,存在y0,xi,yj∈S(i=1,2,…,m;j=1,2,…,m-1),使得 a=φ(y0),ai=φ(xi),bj=φ(yj)(i=1,2,…,m;j=1,2,…,m-1), 于是有 φ(y0)≤Tφ(x1)φ(σ)φ(y1)≤T…≤T φ(xm-1)φ(σ)φ(ym-1)≤Tφ(xm)φ(σ)φ(y0). 对φ(yi)≤Tφ(xi+1),由φ是商序同态得,存在ui,vi+1∈S,ui≤Svi+1(i=1,2,…,m-1),使得 φ(yi)=φ(ui),φ(xi+1)=φ(vi+1)(i=0,1,…,m-1). 于是对φ(xi)φ(σ)φ(yi),有φ(vi)φ(σ)φ(ui),从而有viσui(i=1,2,…,m-1); 对φ(xm)φ(σ)φ(y0),有φ(vm)φ(σ)φ(u0), 从而有vmσu0. 因此, 由ui≤Svi+1,vjσuj(i=0,1,…,m-1;j=1,2,…,m-1),vmσu0得 u0≤Sv1σu1≤S…≤Svm-1σum-1≤Svmσu0,又因为S中任意模σ的闭半拟链的长度均为零, 所以 u0=vi=uj(i=1,2,…,m;j=1,2,…,m-1), 于是有φ(u0)=φ(vi)=φ(uj)(i=1,2,…,m;j=1,2,…,m-1), 即 φ(y0)=φ(xi)=φ(yj)(i=1,2,…,m;j=1,2,…,m-1),由此得,a=ai=bj(i=1,2,…,m;j=1,2,…,m-1), 即T中任意模φ(σ)的闭半拟链的长度也均为零. 定理3设(S,·,≤S),(T,*,≤T)是偏序半群,且S中任意模σ的闭半拟链的长度均为零,φ是S到T的商序满同态,σ为S上的半拟序,≤*是≤S关于σ的偏序扩张, 那么 (2) 若令φ(≤*):={(a,b)∈T×T|(∃x,y∈S)a=φ(x),b=φ(y),x≤*y},则φ(≤*)是≤T关于φ(σ)的偏序扩张. (2) 首先,证明(T,*,φ(≤*))是偏序半群. (i)φ(≤*)自反. 对∀a∈T, 由φ是满的,存在x∈S,使得a=φ(x),由于x≤*x,因此,aφ(≤*)a; (ii)φ(≤*)传递. 对∀a,b,c∈T,∃x,y,z∈S,若aφ(≤*)b,bφ(≤*)c, 则 a=φ(x),b=φ(y),c=φ(z),x≤*y,y≤*z, 于是有x≤*z,从而有aφ(≤*)c; (iii)φ(≤*)反对称.对∀a,b∈T,∃x,y∈S,若aφ(≤*)b,bφ(≤*)a, 则 a=φ(x),b=φ(y),x≤*y,y≤*x, 于是有x=y,从而有φ(x)=φ(y), 即a=b; (iv)φ(≤*)关于T的运算相容.对∀a,b∈T,∃x,y∈S,若aφ(≤*)b, 则 a=φ(x),b=φ(y),x≤*y. 又对∀c∈T,由φ是满的知,存在z∈S,使得c=φ(z),于是对z∈S,x≤*y, 有xz≤*yz,由此得φ(xz)φ(≤*)φ(yz), 即a*cφ(≤*)b*c; 同理可以证明c*aφ(≤*)c*b. 其次, 证明φ(≤*)是≤T的偏序扩张. 对∀a,b∈T, 若a≤Tb,∃x,y∈S,则由φ是满的得 a=φ(x),b=φ(y),φ(x)≤Tφ(y), 由于φ是商序同态,因此,∃u,v∈S,使得 u≤Sv,φ(x)=φ(u),φ(y)=φ(v). 对u≤Sv,因为≤*是≤S关于σ的偏序扩张,所以u≤*v,于是有φ(u)φ(≤*)φ(v),即aφ(≤*)b,因此,≤T⊆φ(≤*),即φ(≤*)是≤T的偏序扩张. 最后,证明φ(≤*)是≤T关于φ(σ)的偏序扩张,即只需证明∀a,b∈T, aφ(≤*)b⟺φ(σ)Cab≠∅. 一方面, 对∀a,b∈T,∃x,y∈S,若aφ(≤*)b, 则 a=φ(x),b=φ(y),x≤*y, x≤Sx1σy1≤S…≤Sxm-1σym-1≤Sxmσy, 由此得 φ(x)≤Tφ(x1)φ(σ)φ(y1)≤T…≤T φ(xm-1)φ(σ)φ(ym-1)≤Tφ(xm)φ(σ)φ(y). 因此,φ(σ)Cφ(x)φ(y)≠∅, 即φ(σ)Cab≠∅; a≤Ta1φ(σ)b1≤T…≤Tam-1φ(σ)bm-1≤Tamφ(σ)b, 由≤T⊆φ(≤*)得aφ(≤*)a1φ(σ)b1φ(≤*)…φ(≤*)am-1φ(σ)bm-1φ(≤*)amφ(σ)b, 于是∃x,y,xi,yj∈S(i=1,2,…,m;j=1,2,…,m-1),使得 x≤*x1σy1≤*…≤*xm-1σym-1≤*xmσy. y0≤Su01σv01≤S…≤Su0,n0-1σv0,n0-1≤Su0,n0σx1, y1≤Su11σv11≤S…≤Su1,n1-1σv1,n1-1≤Su1,n1σx2, y2≤Su21σv21≤S…≤Su2,n2-1σv2,n2-1≤Su2,n2σx3, … ym-2≤Sum-2,1σvm-2,1≤S…≤Sum-2,nm-2-1σvm-2,nm-2-1≤S um-2,nm-2σxm-1,ym-1≤Sum-1,1σvm-1,1≤S…≤Sum-1,nm-1-1σvm-1,nm-1-1≤S um-1,nm-1σxm. 又因为xiσyi(i=1,2,…,m-1),xmσy, 所以有 x=y0≤Su01σv01≤S…≤Su0,n0-1σv0,n0-1≤S u0,n0σx1≤Sx1σy1≤Su11σv11≤S…≤S u1,n1-1σv1,n1-1≤Su1,n1σx2≤Sx2σy2≤Su21σv21≤S …≤Su2,n2-1σv2,n2-1≤Su2,n2σx3≤Sx3σy3≤S, … ym-2≤Sum-2,1σvm-2,1≤S…≤S um-2,nm-2-1σvm-2,nm-2-1≤S um-2,nm-2σxm-1≤Sxm-1σym-1≤S um-1,1σvm-1,1≤S…≤S um-1,nm-1-1σvm-1,nm-1-1≤S um-1,nm-1σxmσy, 即σCxy≠∅, 由≤*是≤S关于σ的偏序扩张,得x≤*y, 从而有aφ(≤*)b. 定理4设(S,·,≤S), (T,*,≤T)是偏序半群,且≤S是可消的,φ是S到T的商序满同态,σ为S上的商半拟序,且S中任意模σ的闭半拟链的长度均为零. 若令 φ(≤*):={(a,b)∈T×T|(∃x,y∈S)a= φ(x),b=φ(y),x≤*y}, 其中≤*是≤S关于σ的可消偏序扩张, 则φ(≤*)是≤T关于φ(σ)的可消偏序扩张. 证明由定理3知,φ(≤*)是≤T关于φ(σ)的偏序扩张. 又对∀a,b,c∈T, ∃x,y,z∈S,若a*cφ(≤*)b*c, 则 a=φ(x),b=φ(y), c=φ(z),φ(xz)φ(≤*)φ(yz). 对φ(xz)φ(≤*)φ(yz),有xz≤*yz,从而有x≤*y,由此得φ(x)φ(≤*)φ(y),即aφ(≤*)b, 因此,φ(≤*)是右可消的; 同理可证φ(≤*)是左可消的. 综上所述,φ(≤*)是≤T关于φ(σ)的可消偏序扩张. [1]谢湘云.序半群引论[M].北京:科学出版社,2001:1-67. XIE Xiangyun. An Introduction to Ordered Semigroups Theory[M]. Beijing: Science Press,2001:1-67. [2]邵海琴,薛占军,雷振亚.偏序半群的偏序扩张[J].纯粹数学与应用数学,2008,24(4):730-736.SHAO Haiqin, XUE Zhanjun, LEI Zhenya. The extension on partial order of partially ordered semigroups[J]. Pure and Applied Mathematics,2008,24(4):730-736. [3]CAO Y L. Quotient ordered homomorphisms of ordered semigroups[J]. Communications in Algebra,2003,31:5563-5579. [4]XIE X Y . An extension of partial orders of commutative partially ordered semigroups[J]. Journal of Mathematical Research and Exposition,2005,25(4):676-682. [5]NAKADA O. Partially ordered Ablian semigroups I[J]. J Fac Sct Hokkaido Univ,1951,11:181-189. [6]NAKADA O. Partially ordered Ablian semigroups II[J]. J Fac Sct Hokkaido Univ,1952,12:73-86. [7]HULIN A J. Extensions of ordered semigroups[J]. Semigroups Forum,1971(2):336-342. [8]HULIN A J. Extensions of ordered semigroups[J]. Czech Math J,1976,26:1-12. [9]邵海琴.偏序半环的偏序扩张[J].宁夏大学学报:自然科学版,2007,28(4):293-296. SHAO Haiqin. The extension on partial order of partially ordered semirings[J]. Journal of Ningxia University: Natural Science Edition,2007,28(4):293-296. [10]邵海琴,何万生,杨随义,等.偏序半群的同态和商序同态的若干重要性质[J].兰州理工大学学报,2011,37(5):137-141. SHAO Haiqin, HE Wansheng, YANG Suiyi, et al. Some important properties on homomorphisms and quotient ordered homomorphisms of partially ordered semigroups[J]. Journal of Lanzhou University of Technology,2011,37(5):137-141. [11]邵海琴,何万生,郭莉琴,等.可换偏序半群的同态和商序同态的若干重要性质[J].浙江大学学报:理学版,2013,40(4):367-370. SHAO Haiqin, HE Wansheng, GUO Liqin, et al. Some important properties on homomorphisms and quotient ordered homomorphisms of commutative partially ordered semigroups[J]. Journal of Zhejiang University: Science Edition,2013,40(4):367-370. [12]CAO Y L. Decompositions and pseudo-orders of ordered semigroups[J]. Semigroups Forum,2004,68:177-185. [13]邵海琴,何万生,郭莉琴.偏序半群的半拟序、正则同余与商序同态[J].宁夏大学学报:自然科学版,2015, 36(2):109-114. SHAO Haiqin, HE Wansheng, GUO Liqin. Semi-pseudoorder, regular congruence and quotient ordered homomorphism of partially ordered semigroups[J]. Journal of Ningxia University: Natural Science Edition,2015,36(2):109-114. The extension on cancellative partial order and quotient ordered homomorphism of cancellative partially ordered semigroup. SHAO Haiqin, GUO Liqin (SchoolofMathematicsandStatisticsInstitute,TianshuiNormalUniversity,Tianshui741001,GansuProvince,China) This paper studies the cancellative partial ordered extension and properties of quotient ordered homomorphisms of cancellative partially ordered semigroups(CPOS). The notion on quotient semi-pseudoorder of partially ordered semigroup(POS) is introduced. With the quotient semi-pseudoorder of CPOS and using the method of partial ordered extension of POS, the sufficient condition for extending a cancellative partial order of CPOS to another cancellative partial order is derived. It is also shown that quotient ordered homomorphism of partially ordered semigroup POS can be depicted by semi-pseudoorderσ, closed semi-pseudochain of moduloσ, quotient semi-pseudoorder, partial ordered extension of partially ordered semigroup, and cancellative partial ordered extension of CPOS. Some important conclusions are obtained. cancellative partially ordered semigroup; semi-pseudoorder; quotient semi-pseudoorder; closed semi-pseudochain; partial ordered extension; cancellative partial ordered extension; quotient ordered homomorphism 2014-10-20. 甘肃省教育厅科学研究基金项目(1108B-03);天水师范学院中青年教师科研资助项目(TSA1311). 邵海琴(1971-),ORCID:http://orcid.org/0000-0002-2409-9696,女,硕士,副教授,主要从事偏序代数研究,E-mail:shaohq12@163.com. 10.3785/j.issn.1008-9497.2016.05.002 O 152.7 A 1008-9497(2016)05-512-05