一类带有对数非线性项的拟线性椭圆方程解的存在性及多重性

刘晓莉,贾 高

(上海理工大学 理学院,上海 200093)

§1 引言

考虑如下拟线性椭圆方程弱解的存在性和多重性

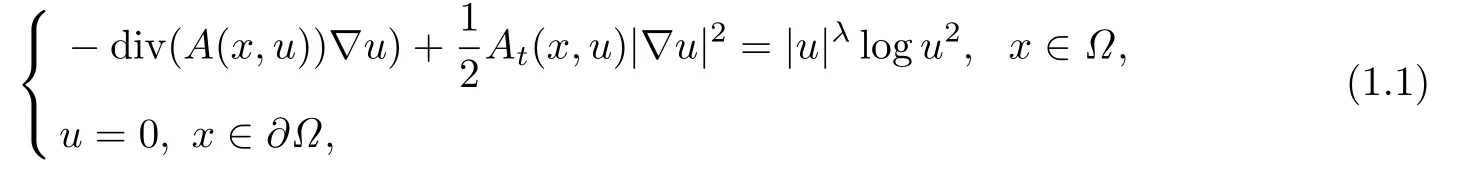
其中Ω ⊂RN是一个具有光滑边界的有界区域,N ≥2,λ ∈(1,2*-1),A(x,t),At(x,t)是RN ×R上的Carath´eordory函数.方程(1.1)和Schrödinger方程的驻波解是密切相关的,并且广泛应用在等离子体物理学,量子光学,量子力学和超流体理论等领域的研究中(见[1-2]).

问题(1.1)对应的自然泛函为

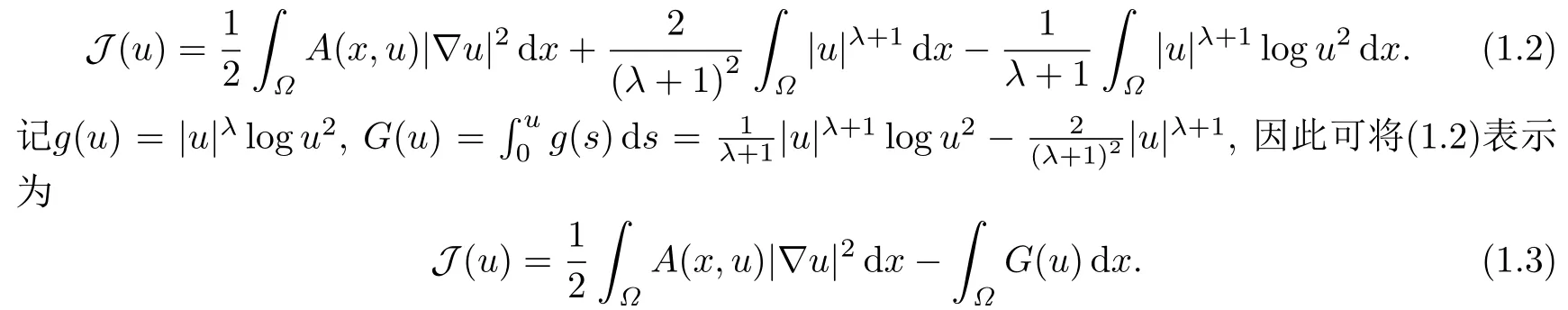
容易看出,|g(u)| ≤C1(1+|u|θ),θ ∈(λ,2* -1),C1＞0,所以对(Ω),关于u是C1的(见[3]).然而,由于泛函的主体部分中有函数A(x,t),导致泛函在(Ω)上有可能不是良定义的.进一步发现,即使A(x,t)是光滑有界的正函数,这时泛函J在(Ω)是良定义的,但是如果,J只能在方向上是Gâteaux可导的.

近年来,一些学者通过使用非光滑临界点理论[4-12]研究如下类型问题

例如,在[6]和[10]中,Candela,Palmieri和Salvatore在有界区域考虑问题(1.4),非线性项g(x,t)关于t满足合适的增长条件,利用弱形式的山路引理和对称山路定理,证明解的存在性和多重性.进一步,Candela 和Salvatore在[8]中证明了当Ω是无界区域时,问题(1.4)径向解的存在性.而带有对数非线性项的Schrödinger方程也引起了很多学者的兴趣,并得到了系列重要成果,见[13-19].

受到上述及相关成果的启发,对函数A(x,t)提出合适的条件,使泛函在空间上是C1的.因为泛函可能不满足经典的(CPS)条件[9],将使用弱形式的(CPS)c条件,以及与之对应的山路引理和对称山路定理.尽管本文的非线性项是对数形式,但是它并不能满足之前很多文献对于非线性项的要求,比如AR条件,这也是本文的创新点和需要克服的难点.

在本文中,假设函数A(x,t)满足以下条件.(A0)A(x,t)是C1的Carath´eordory函数,即

A(·,t):(x,t)∈R对于所有t ∈R是可测的,

A(x,·):t ∈R(x,t)∈R对几乎处处的x ∈Ω是C1的;(A1) 当t有界时,A(x,t)和At(x,t)是本性有界的,即

(A5)A(x,t)=A(x,|t|) a.e.x ∈Ω,对所有t ∈R.

注记1.1经过简单计算可得,若a(x)是可测函数,且满足0＜a1≤a(x)≤a2,那么A(x,t)=a(x)(1+|t|λ-1)满足条件(A0)-(A5).

注记1.2根据条件(A1)-(A4),可得当|t|≥R0时,有

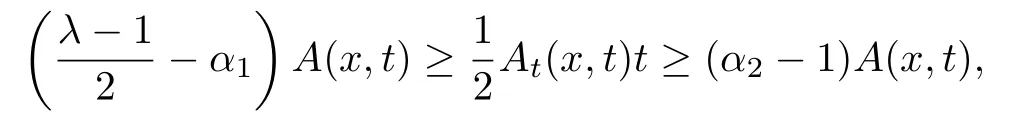
经过简单的计算,可知存在正常数C2,C3,当|t|≥R0时,成立

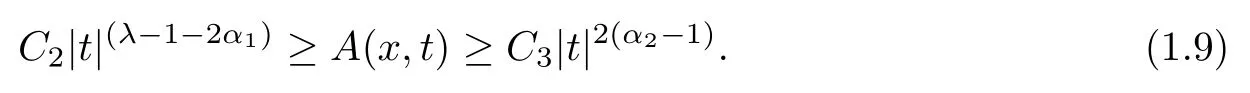
注记1.3因为

故存在正常数C4,C5,成立

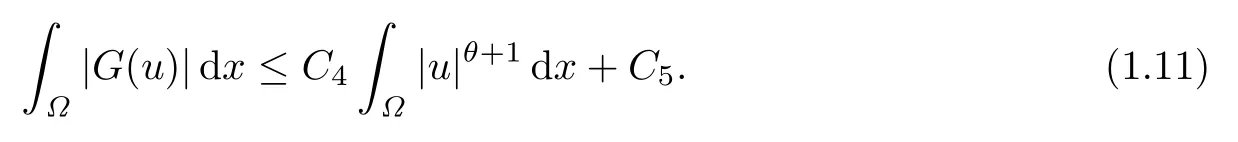
注记1.4由于

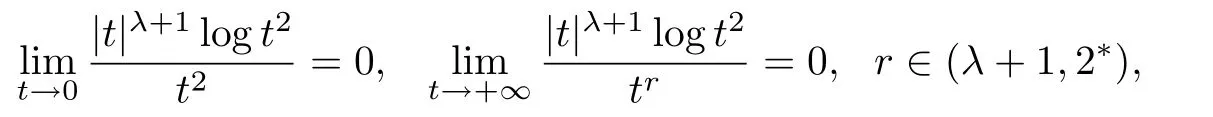
故对于任意的∈＞0,存在常数C∈,成立

本文的主要结果如下.

定理1.1设N ≥2,λ ∈(1,2*-1),函数A(x,t)满足条件(A0)-(A4),则问题(1.1)存在一个山路解.

定理1.2设N ≥2,λ ∈(1,2*-1),函数A(x,t)满足条件(A0)-(A5),则问题(1.1)存在无穷多个非平凡解.

§2 预备知识和主要引理

首先说明文中的一些符号.Lp(Ω)(1≤p ＜+∞)和(Ω)是标准的Lp空间和Hilbert空间,它们的范数分别定义为是Lebesgue可测且本性有界的函数的集合,范数定义为本文工作空间,它的对偶空间记为(X′,‖·‖X′),在X上赋予范数‖·‖X=‖·‖H+|·|∞.在本文中,Ci,i ∈{1,2,3,···},表示正常数,εn表示当n →∞时的无穷小量,εk,n表示与k有关的当n →∞时的无穷小量.

定义2.1设Z是Banach空间,泛函I在Z上的Frechet导数dI存在,称序列{un} ⊂Z是I的一个(CPS)c序列,如果该序列满足

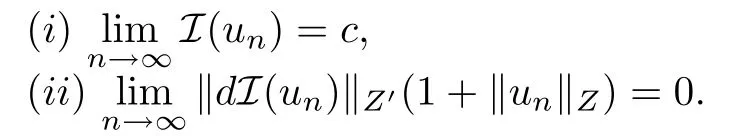
定义2.2设Z是Banach空间,若存在Banach空间(B,‖·‖B),使得(连续嵌入).称泛函I在水平c上满足(wCPS)c条件,如果对于I的每个(CPS)c序列{un} ⊂Z,都存在{un}的子列(仍记为{un})以及u ∈Z,使得

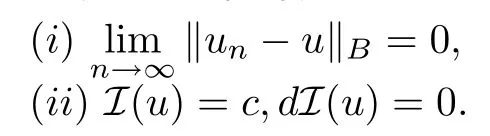
因为(wCPS)c条件(i)只表明在‖·‖B意义下的收敛,故I的临界点集在‖·‖B意义下是紧的,但在‖·‖Z意义下不能保证是紧的.幸运的是,在这个弱条件下,形变引理和一些临界点定理仍然成立[6-7].

定理2.1(山路引理) 设Z是Banach空间,且存在Banach空间(B,‖·‖B),使得.泛函I ∈C1(Z,R),I(0)=0,满足(wCPS)c条件,且存在正常数r0,ρ0,存在点e ∈Z,且

(i) 当u ∈Z,且‖u‖B=r0时,有I(u)≥ρ0,

(ii)‖e‖B ＞r0,且I(e)＜ρ0,

则I有一个山路临界点u* ∈Z,且I(u*)≥ρ0.

定理2.2(对称山路定理) 设Z是Banach空间,且存在Banach空间(B,‖·‖B),使得.设I ∈C1(Z,R)是偶泛函,满足(wCPS)c条件,I(0)=0.存在ρ ＞0,使得

(i)存在Z的闭子集Vρ和Wρ,满足

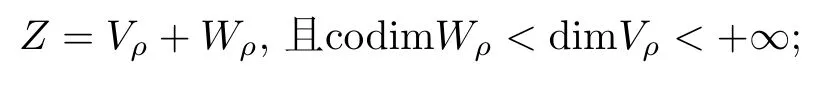
(ii)存在常数rρ ＞0,当u ∈Wρ,且‖u‖B=rρ时,有I(u)≥ρ;

(iii)存在常数Rρ ＞0,当u ∈Vρ,且‖u‖Z ≥Rρ时,有I(u)≤0.

则I在Z内至少有一对临界点,且临界值位于

注记2.1记Γρ={γ:Z →Z |γ是一个奇的连续映射,当u ∈Vρ且‖u‖Z ≥Rρ时,γ(u)=u},根据文献[6],对γ ∈Γρ有

下面给出可以获得序列在空间强收敛的引理.

引理2.1[20]设W是一致凸的Banach空间,算子A ∈C(W,W′),且对任意的u,v ∈W,存在正常数a,成立

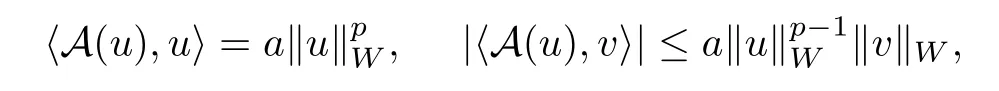
其中p ∈(1,+∞).如果当j →+∞时序列{uj}⊂W满足

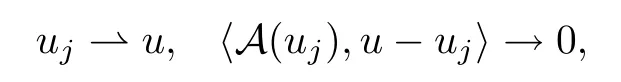
则{uj}在W中有强收敛子列.

下面的引理将保证在某些条件下W1,p(Ω)中函数的有界性.

引理2.2[6]设Ω是RN内的有界区域,且有光滑边界∂Ω.对于v ∈W1,p(Ω)(1≤p ≤N),如果存在b ＞0和k0∈N使得

§3 泛函J 的正则性

容易证明,在空间X上,泛函J的Gâteaux导数为

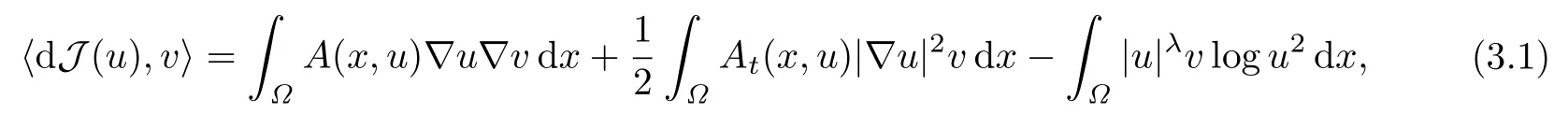
且dJ是泛函J的Frechet导数,dJ在‖·‖H意义下是连续的.

引理3.1设u ∈X,{un} ⊂X,|un|∞＜M,且当n →∞时,‖un -u‖H →0,则成立|J(un)-J(u)|→0和‖dJ(un)-dJ(u)‖X′ →0.

证记

则J=J1-J2.由注记1.3,J2在X上是C1的,因此只要分析J1的连续性和可微性.

设{un}是满足条件的序列,由于

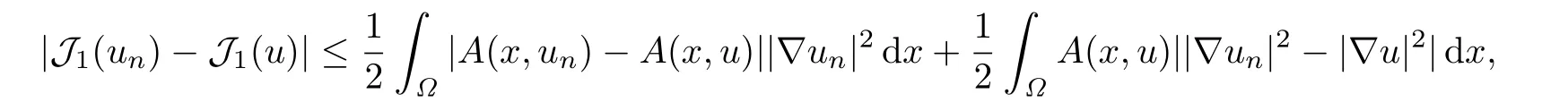
根据|un|∞＜M以及(A0),(A1),那么存在正常数C6,使得

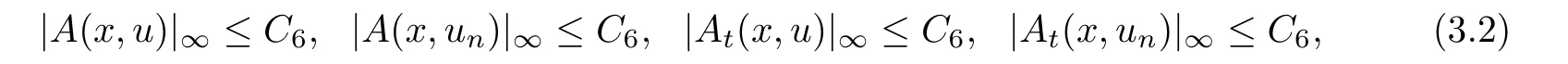
且当n →∞时,有un →ua.e.x ∈Ω.利用(3.2),‖un-u‖H →0和Lebesgue控制收敛定理可得

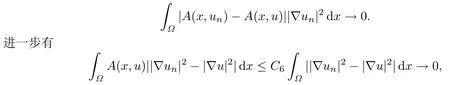
即|J1(un)-J1(u)|→0,故泛函J1是连续的.

另一方面,对任意v ∈X,且‖v‖X=1,有

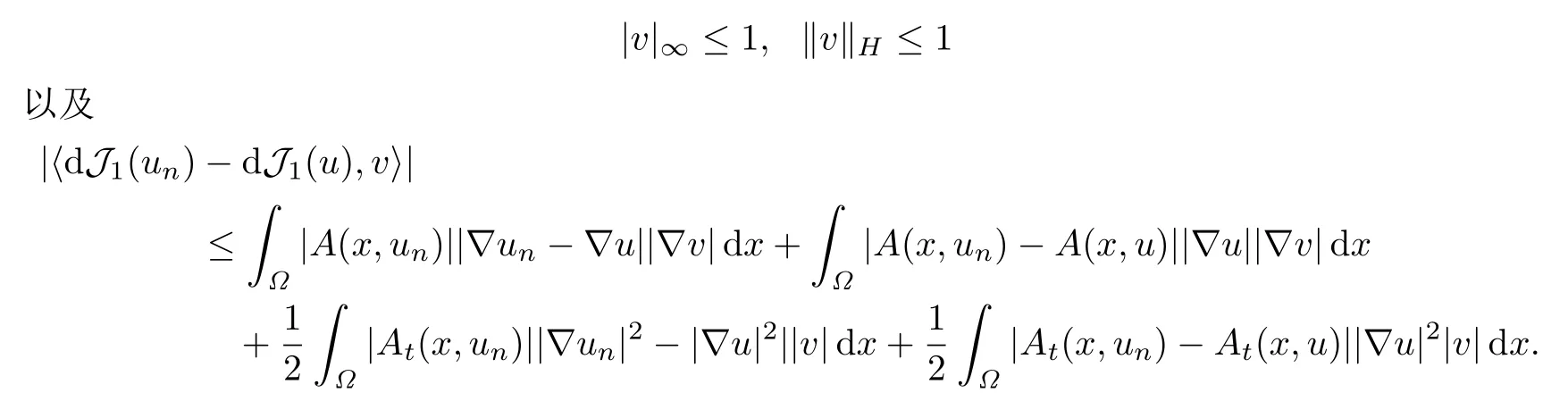
因为‖un-u‖H →0,由式(3.2),利用Hölder不等式和Lebesgue控制收敛定理,可得

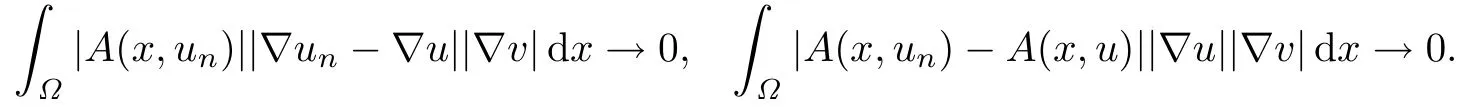
重复证明J1连续性的步骤,可得

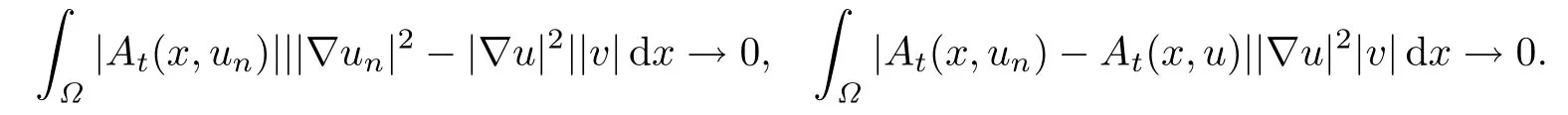
综合分析可知,对任意v ∈X,且‖v‖X=1,当n →∞时,有|〈dJ1(un)-dJ1(u),v〉| →0一致成立,故‖dJ1(un)-dJ1(u)‖X′ →0.

§4 山路解的存在性

引理4.1设N ≥2,λ ∈(1,2*-1),A(x,t)满足条件(A0)-(A4),则对任意c ∈R,泛函J满足(wCPS)c条件.

证对c ∈R,设{un}⊂X为J的(CPS)c序列,即

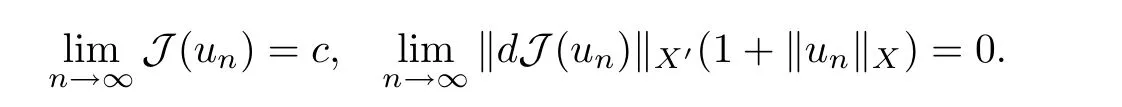
Step 1证明{un}在(Ω)上是有界的.

由于

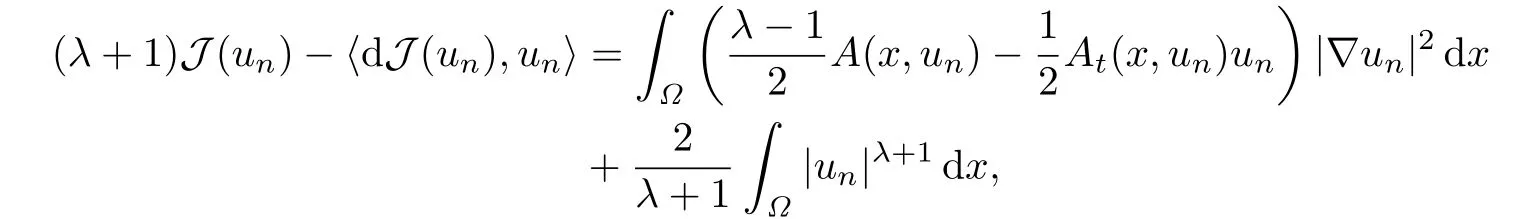
结合(A2),(A3),从上式可得

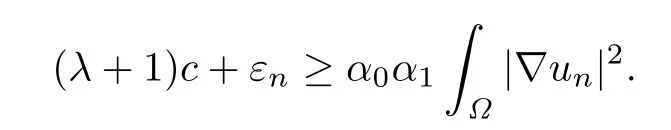
因此{un}在(Ω)上有界,故存在{un}的子列(仍记为其本身)及(Ω),当n →∞时有

Step 2证明u ∈L∞(Ω).

反证,如果uL∞(Ω),则有

若第一种情况成立,则对于固定的k ∈N,k ＞R0(R0由(A4)给出),有meas()＞0,其中.定义,考虑函数

故存在nk ∈N,当n ≥nk时,有

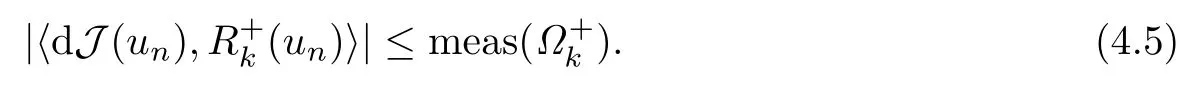
利用(A4)可得

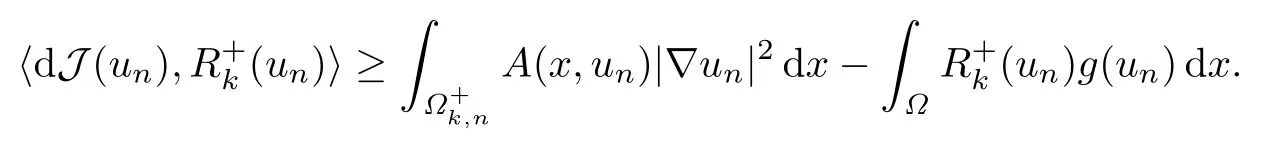
进而利用(A2),有

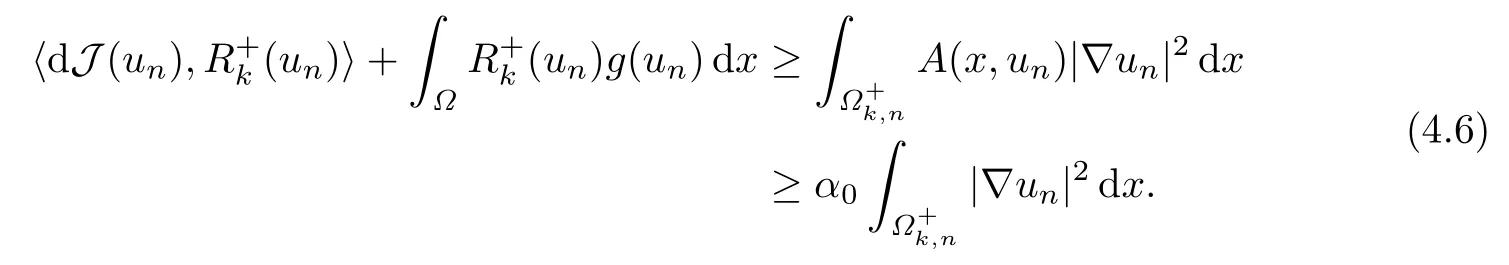
注记1.3表明

从而利用Lebesgue控制收敛定理有

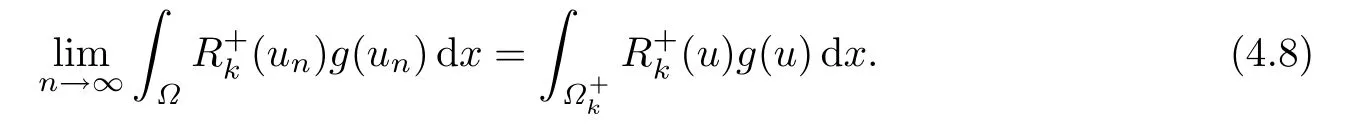
由(4.2)-(4.8),可得

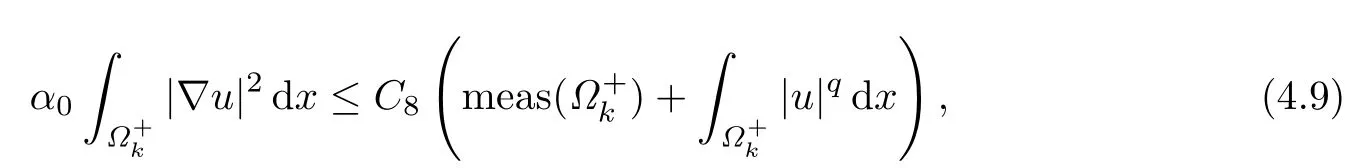
由于上式对所有k ＞R0都成立,利用引理2.2便得到矛盾.因此第一种情况不成立.

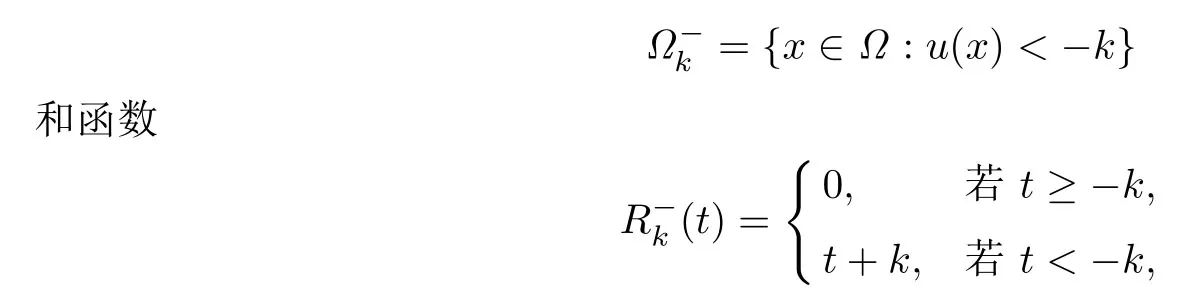
重复以上步骤,同样可以得到矛盾.因此第二种情况也不成立,故u ∈L∞(Ω).

Step 3构造新的(CPS)c序列.

定义函数Tk:R→R

下面证明当k ≥max{|u|∞,R0}+1时,{Tk(un)}也是(CPS)c序列.

定义Ωk={x ∈Ω:|u(x)|＞k}和Ωk,n={x ∈Ω:|un(x)|＞k},由函数Tk的定义可得

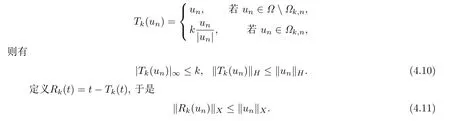
因为k ＞|u|∞,所以有

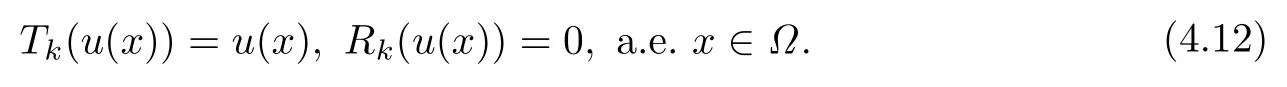
再由(4.1),当n →∞时,有

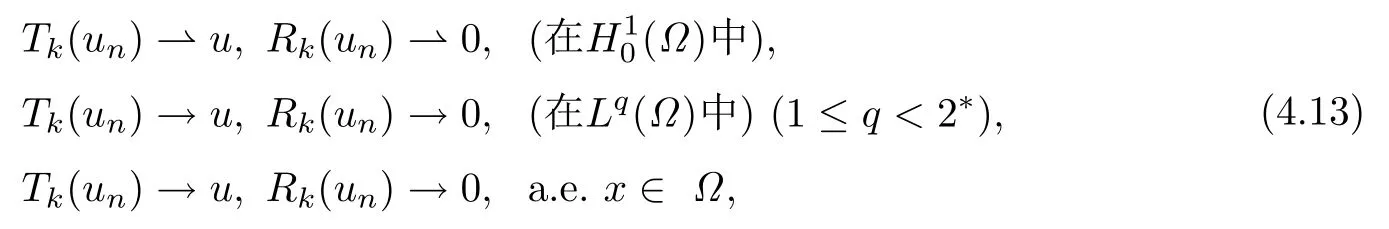
且由k ＞|u|∞可得

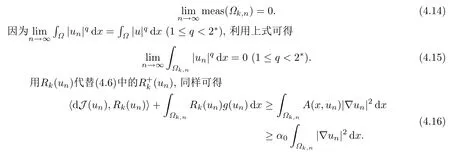
从(4.14)和(4.15)有

由(4.11)有

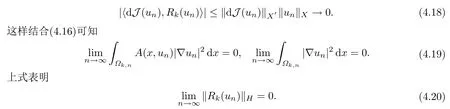
根据Tk(un)的定义有

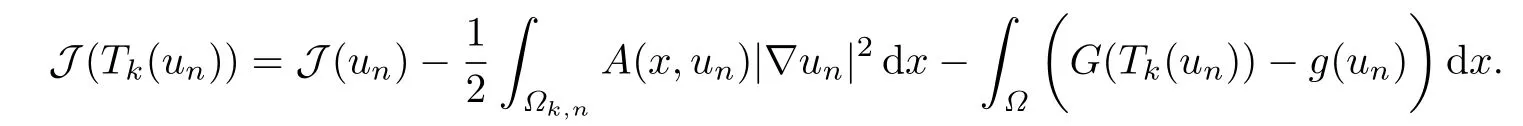
利用(4.14),(4.15)和注记1.3得到

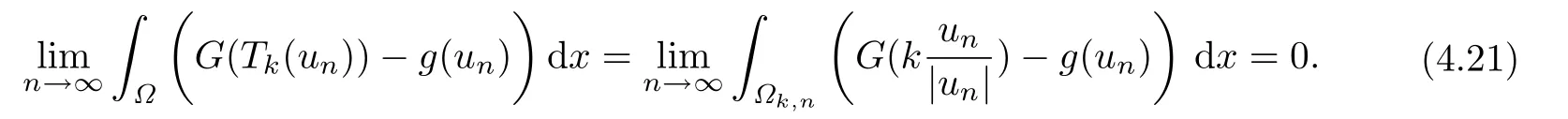
结合(4.19)可知

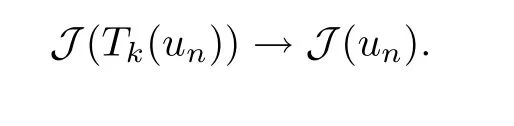
任取v ∈X,且满足‖v‖X=1,有

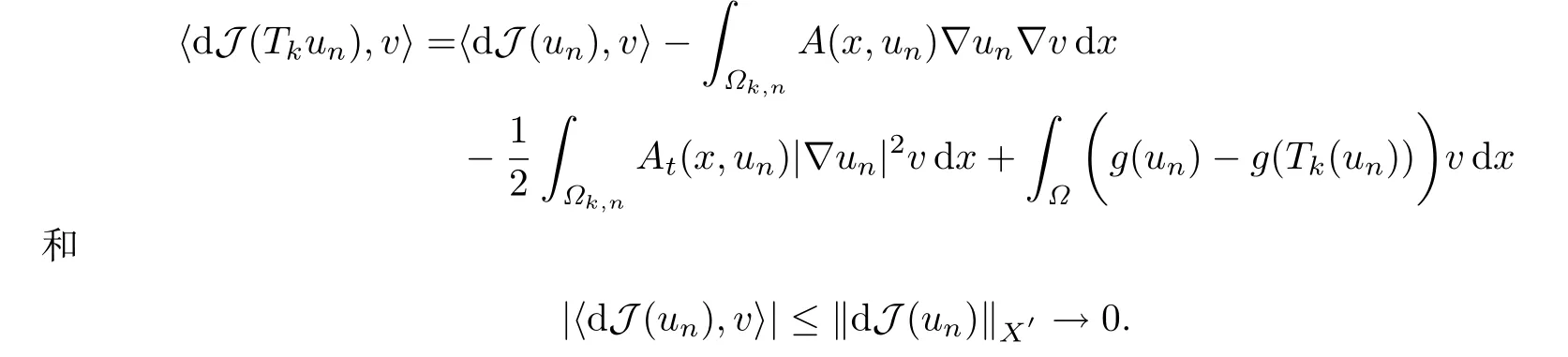
运用类似于证明(4.21)的方法可得

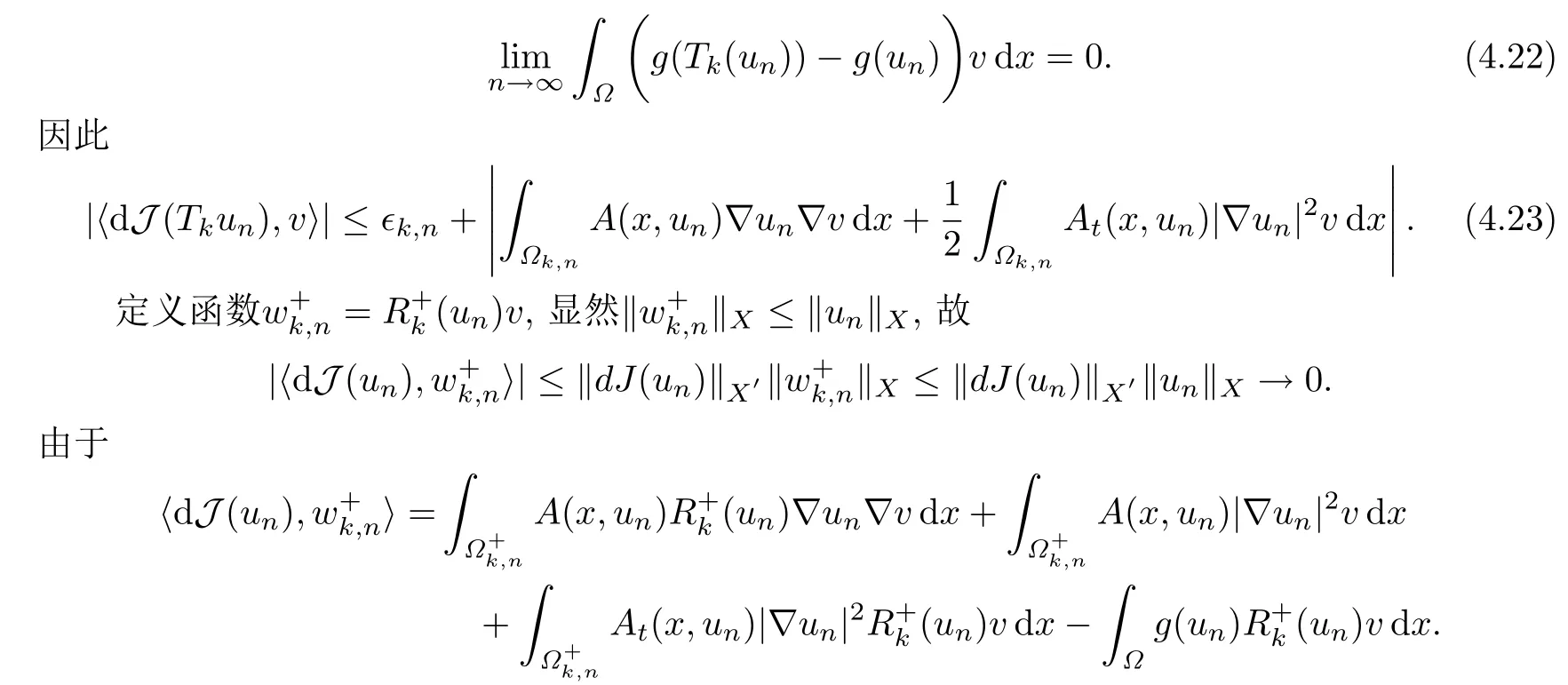
注意到v ∈L∞(Ω),综合(4.19),(4.12)和(4.8)可得

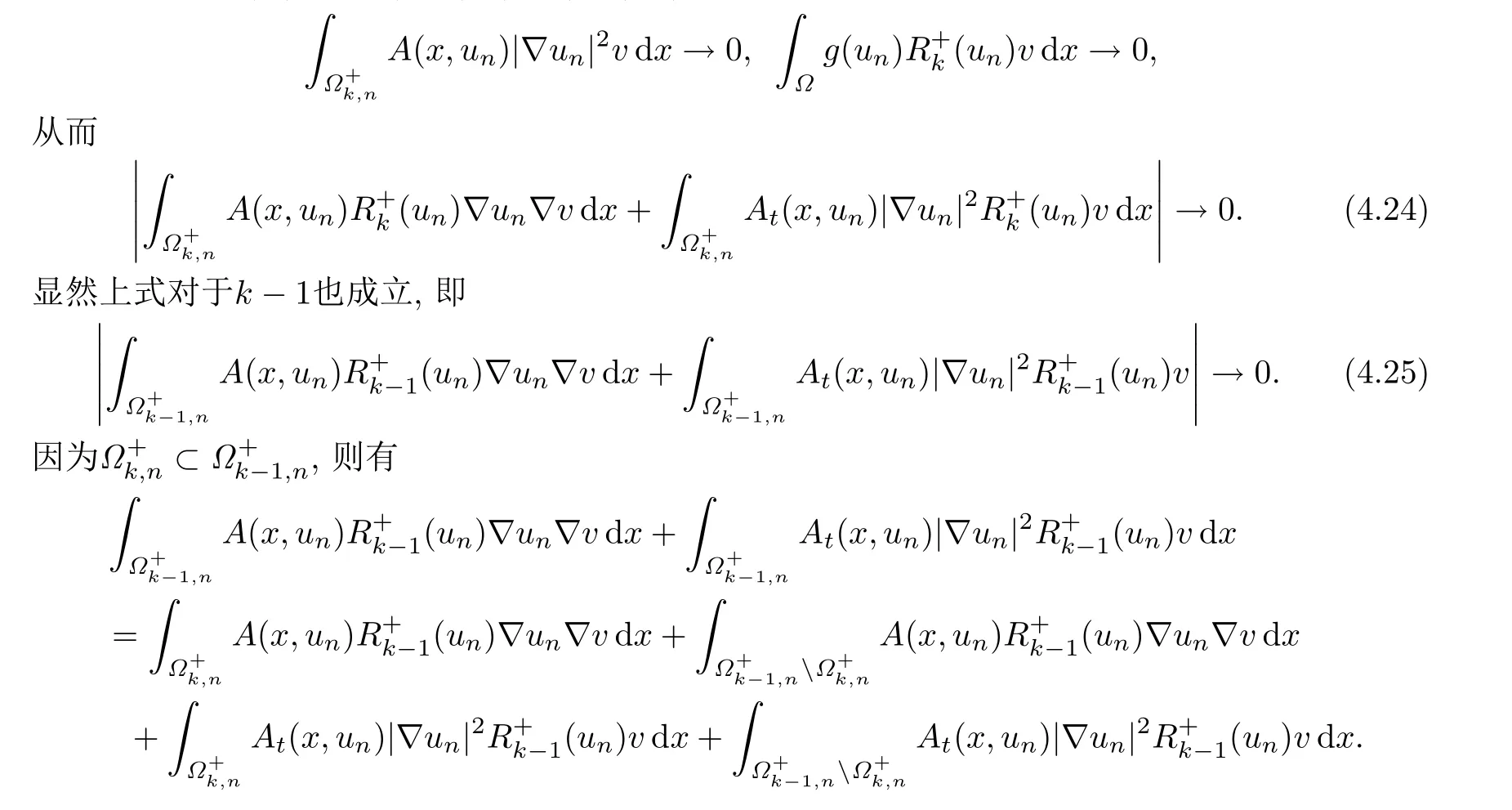
由(4.23),当n →∞时,有〈dJ(Tk(un)),v〉→0,所以序列Tk(un)是J的(CPS)c序列.

Step 4证明当n →∞时,有‖Tk(un)-u‖H →0和‖un-u‖H →0.

定义函数

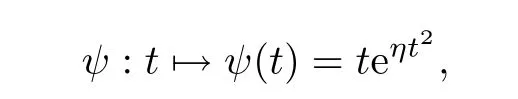
定义函数vk,n=Tk(un)-u,由(4.10)和|u|∞＜k,知|vk,n|∞＜2k.由ψ的定义和(4.13),当n →∞时有

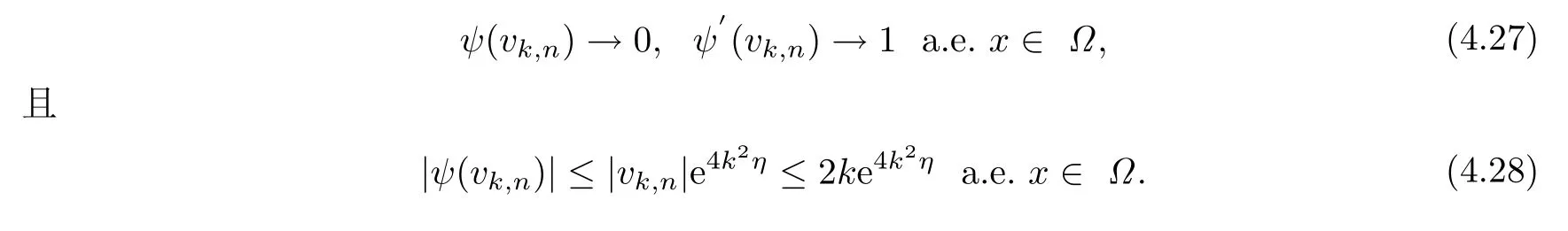
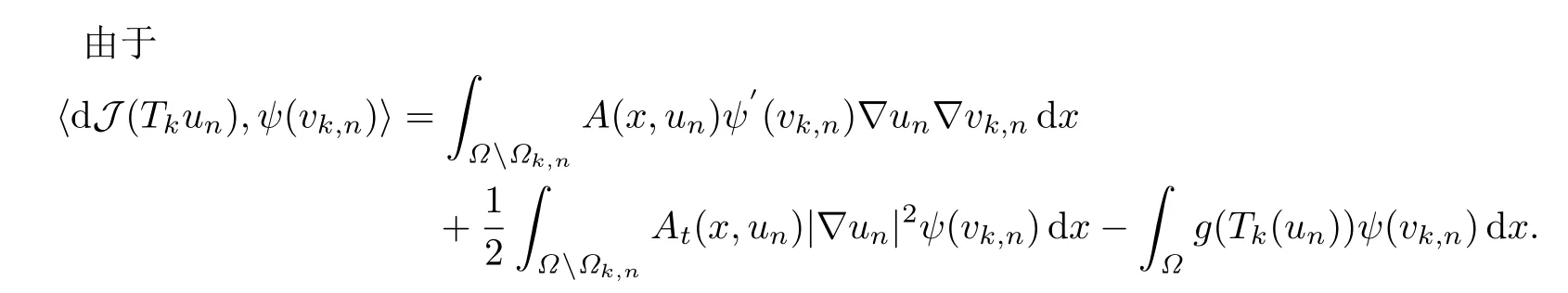
根据Step 2的结论,可得

由(4.10),(4.27),(4.28)和注记1.3,利用Lebesgue控制收敛定理有

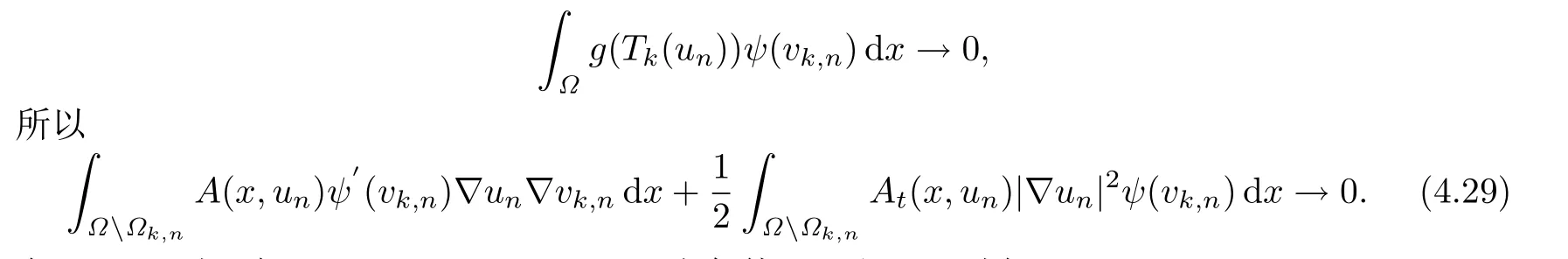
在Ω Ωk,n上,有|un(x)|≤ka.e.x ∈Ω,由条件(A1)和(A2)则有

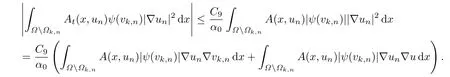
由条件(A1)和(4.27),利用Hölder不等式和Lebesgue控制收敛定理可得

根据{un}和{vk,n}在(Ω)上的有界性,以及{A(x,un)}在Ω Ωk,n上有界,运用(A1),Hölder不等式和Lebesgue控制收敛定理可得

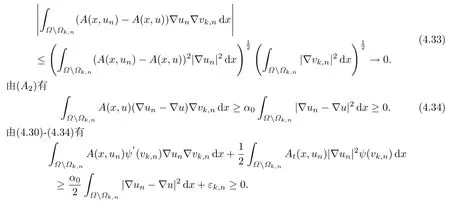
结合(4.29)可得

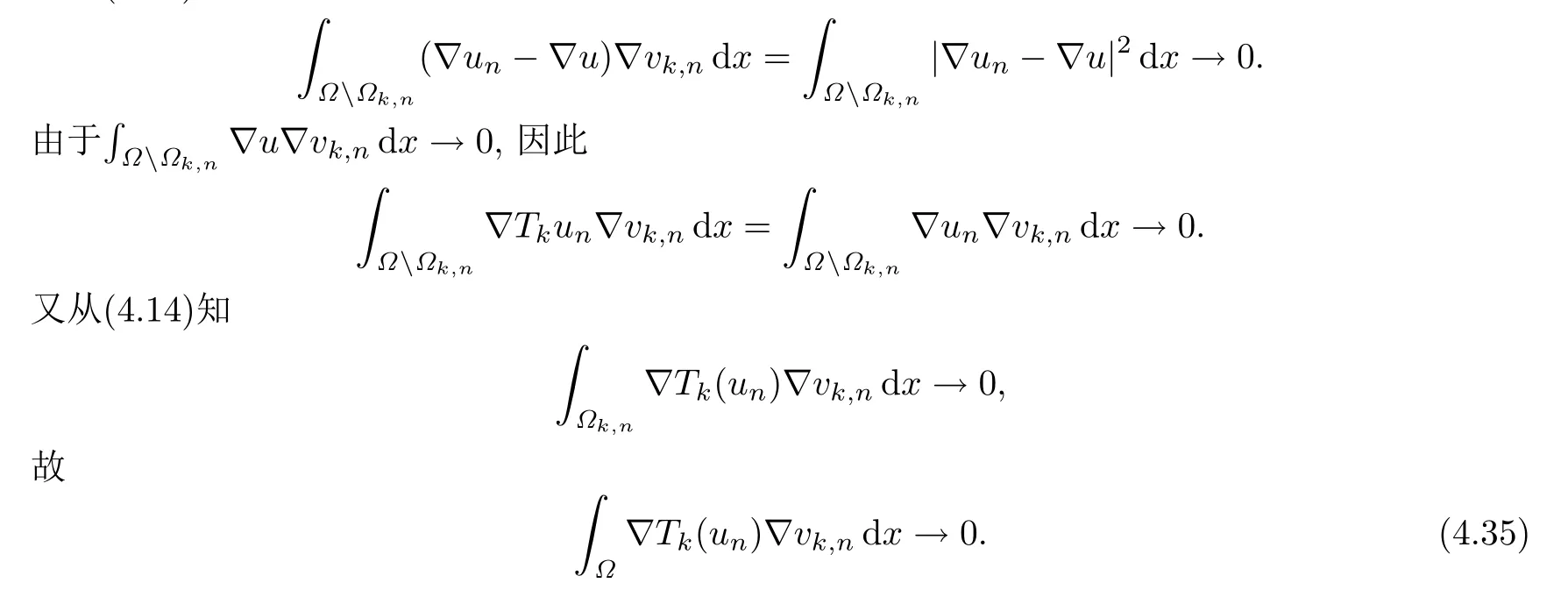
对(Ω),定义算子L(u)满足

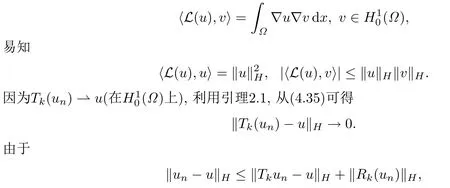
结合(4.20),当n →∞时有

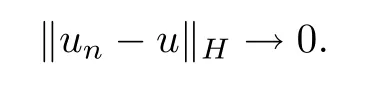
Step 5证明J(u)=c,dJ(u)=0.

由上述讨论可知,当k充分大时,{Tk(un)}是(CPS)c序列,且对所有n ∈N,有|Tk(un)|∞≤k,‖Tk(un)-u‖H →0,由引理3.1可知J(u)=c,dJ(u)=0.

引理4.2设N ≥2,λ ∈(1,2*-1),A(x,t)满足(A0)-(A4),则泛函J满足山路引理的几何条件.

证由(A2),(1.12)和嵌入不等式有

取∈足够小,使得,故|∇u|2充分小时,即‖u‖H充分小时,就有J(u)＞0.

设φ1为(-Δ,(Ω))的第一特征函数,不妨设φ1＞0,由注记1.2,对s ＞0有

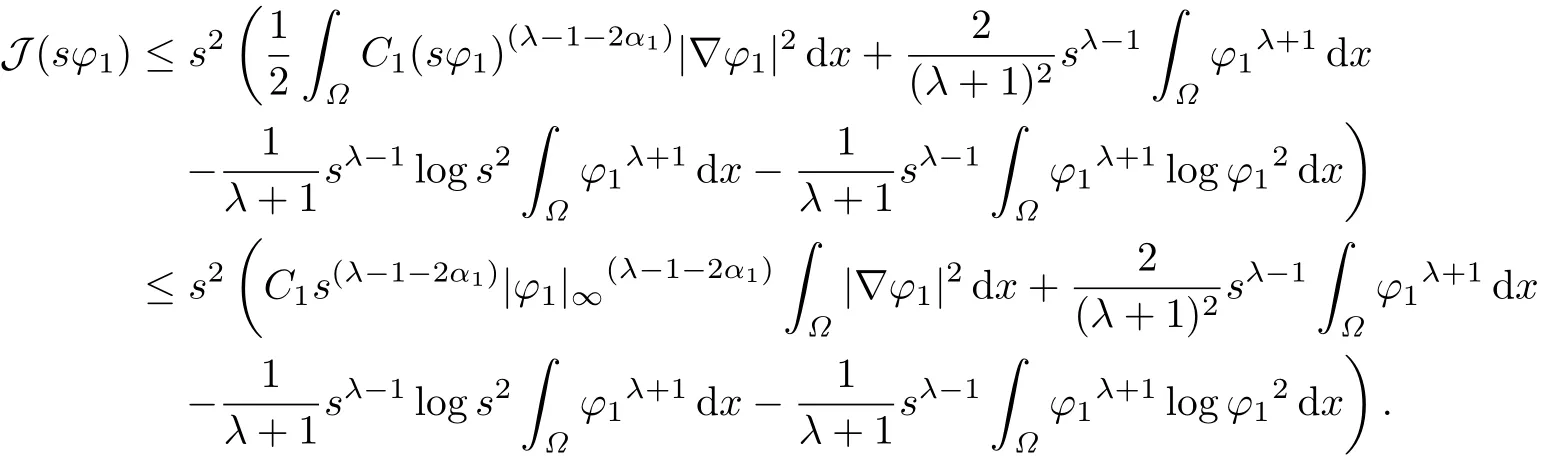
结合引理4.1和引理4.2,根据定理2.1知,J存在一个山路临界点,故问题(1.1)存在一个非平凡解,即定理1.1 得证.

§5 解的多重性

引理5.1对X的任意有限维子空间V,都存在R ＞0,当u ∈V,且‖u‖X ≥R时,有J(u)≤0,并且J在V内是上有界的.

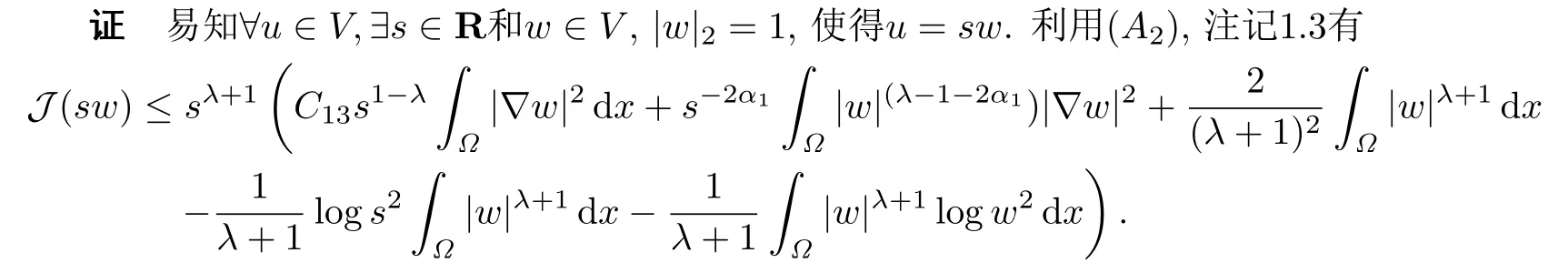
由于有限维空间所有范数是等价的,故上面关于w的所有积分都是有界的.又λ ＞1,α1＞0,因此当s →+∞时,J(sw)→-∞,故存在R ＞0,当‖u‖X ≥R时,有J(u)≤0.

引理5.2对于任意给定ρ ＞0,则存在m ∈N和rm ＞0,当,且‖u‖H=rm时,有J(u)≥ρ.

证从(A2)和注记1.3可得

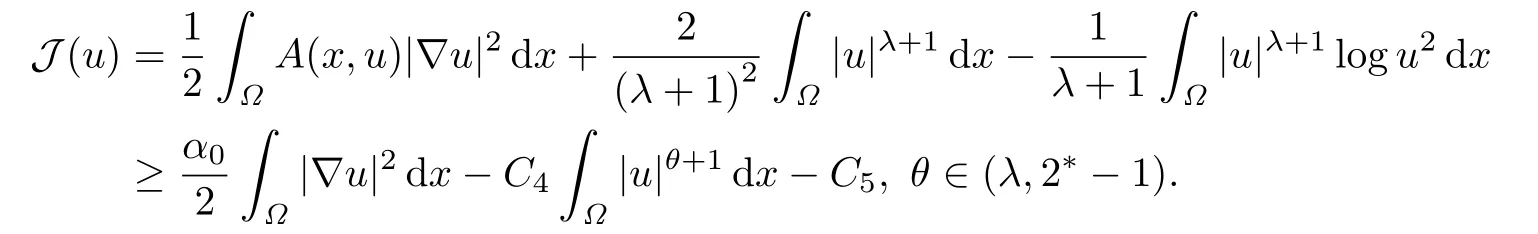
记β=θ+1,选择r ∈(0,β)满足,由插值不等式和,则

易知J是偶泛函.对给定ρ0,由引理5.2知存在m0∈N和rm0＞0,当,且‖u‖H=rm0时,有J(u)≥ρ0.对于任意m1＞m0,显然有codimHm0＜dimVm1,则由引理5.1,注记2.1,定理2.2,可得J存在一对临界点,且临界值位于区间[ρ0,ρ1],其中选取新的,重复上述过程,可以找到另一对临界点,从而问题(1.1) 有无穷多个非平凡解.至此,定理1.2得证.