关于图的距离无符号拉普拉斯谱半径的下界

朱银芬，王国平，陈 星

(1.新疆工程学院数理学院，乌鲁木齐 830029;2.新疆师范大学数学科学学院，乌鲁木齐830017)

如果一个连通图G的点集是V(G)={v1，v2，…，vn}，那么图G的距离矩阵D(G)=(dij)，其中dij表示点vi与vj之间的距离.令TrG(vi)表示点vi到图G中其它所有点的距离之和，Tr(G)表示对角线位置的元素是TrG(vi)的对角矩阵.

图G的距离拉普拉斯矩阵及距离无符号拉普拉斯矩阵分别被表示为LD(G)=Tr(G)-D(G)与QD(G)=Tr(G)+D(G)，它们的最大特征值λL(G)和λQ(G)分别是图G的距离拉普拉斯谱半径与距离无符号拉普拉斯谱半径．

Aouchiche和Hansen在文献[1]中引入了图的距离拉普拉斯谱与距离无符号拉普拉斯谱的概念，并且在文献[2]中证明了树中星图具有最小距离拉普拉斯谱半径.近年来，关于距离拉普拉斯谱与距离无符号拉普拉斯谱的研究已经有了长足的进展.Xing与Zhou[3]确定了双圈图中具有最小距离谱半径与最小距离无符号拉普拉斯谱半径的唯一图.文献[4]确定了在树、单圈图、双圈图、给定悬挂点数与连通度的图中具有最小距离无符号拉普拉斯谱半径的图.Liu与Lu[5]确定了给定团数的距离无符号拉普拉斯谱半径的界.Lin和Zhou[6]刻画了在给定悬挂点数与边连通度的图中具最小的距离拉普拉斯谱半径的唯一图的特性.牛爱红等[7]确定了给定匹配数或给定连通度的二部图中具有最小距离拉普拉斯谱半径的极图．

本文确定了给定匹配数的图的距离无符号拉普拉斯谱半径的下界．

1 引理

先给出一些已知的结果．

引理1[1]图G是连通图，若uv∉E(G)，那么λQ(G+uv)<λQ(G)．

引理2[1]设图G是n阶连通图，那么λQ(G)≥λQ(Kn)=2(n-1)．

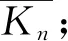
引理4[8]设A1与A2是n阶实对称矩，那么

λn(A2)+λi(A1)≤λi(A1+A2)，

其中λi(A)是A的第i大特征值．

引理5[8]设A是n阶实对称矩阵，M是A的s(s

λi+n-s(A)≤λi(M)≤λi(A)(1≤i≤s)，

其中λi(A)是A的第i大特征值.

若有X⊂V(G)，那么图G的子图G-X是将图G的X中的点与X点相关联的边同时删除后得到的.图G的一个匹配是图G中不相邻的边的集合，那么所有匹配中含有最大的边数叫做图G的匹配数.若图G的某个连通分支的点数是奇数，那么称这个连通分支是图G的奇连通分支;否则，称这个连通分支是偶连通分支．

引理6[9-10]如果图G是匹配数为m的n阶图，那么

n-2m=max{o(G-X)-|X|:X⊂V(G)}，

其中o(G-X)是图G-X的奇连通分支数．

引理7[11]如果图G是连通图，那么λQ(G)>λL(G)．

2 定理及推论

≅

Kn，则由引理1知λQ(G)>λQ(Kn)．

设G-X0的所有连通分支为H1，H2，…，Hk，Hk+1，…，Ht，其中H1，H2，…，Hk是G-X0的奇连通分支，Hk+1，…，Ht是G-X0的偶连通分支．

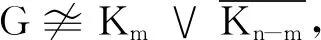
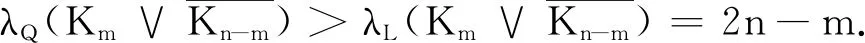
这样，λQ(G)>2n-m．

下面假定s

情况1t=k.

在这种情况下G-X0的所有连通分支H1，H2，…，Hk都为奇连通分支.设|V(Hi)|=ni，则ni是奇数(i=1，2，…，k)．

下面先就G≅Ks∨(Kn1∪Kn2∪…∪Knk)的情况进行验证．

为方便书写，不妨假定n1≤n2≤…≤nk.若n1=…=nk=1，则n=k+s．

注意到n-2m=k-s，这样就有s=m，这与s

令M={v1u1，v2u2，…，vsus}∪Mp∪Mp+1∪…∪Mk，则M就是G的一个匹配．这样，

注意到当p≤i≤k时，ni≥np.因此，

若p≥3，则n1=n2=1.设u与v分别是Kn1与Kn2中的那个点.在QD(G)中取2×2阶主子矩阵:

因为k≥3，所以m≥s+1，进而

TrG(v)=TrG(u)=

s+2(n-s-1)≥2n-m-1，

令

由引理4与引理5，得到

λQ(G)≥λQ(A)≥λQ(A′)=2n-m+1>2n-m.

若p=2，那么n1=1，而对于所有的2≤i≤k都有ni≥3.设u∈Kn1且v∈Ks，类似可得，在QD(G)中取2×2阶主子矩阵：

因为k≥3，于是得到m≥s+2.进而

TrG(v)=s+2(n-s-1)≥2n-m，

且

TrG(u)=n-1．

令

由引理4与引理5，得到

λQ(G)≥λQ(B)≥λQ(B′)=

2n-m.

若p=1，则对于所有的1≤i≤k都有ni≥3.下面针对k≥3的取值情况分类讨论．

若k≥4，设u和v是Kn1中不同的两个点.在QD(G)中取2×2阶主子矩阵:

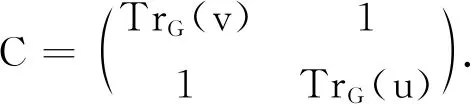
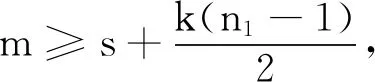
TrG(v)=TrG(u)=
s+n1-1+2(n-s-n1)≥2n-m.

令

由引理4与引理5得

λQ(G)≥λQ(C)≥λQ(C′)=

2n-m+1>2n-m.

当k=3且n3=3时，设u∈Kn1，v∈Kn2.在QD(G)中取2×2阶主子矩阵：

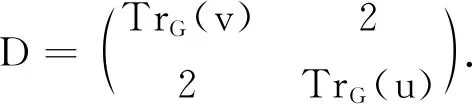
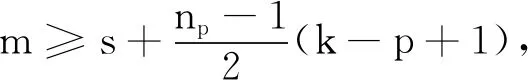
TrG(v)=TrG(u)=s+n1-1+2(n-s-n1)
≥2n-s-4≥2n-m-1.

令

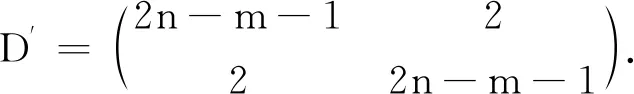
由引理4与引理5，得

λQ(G)≥λQ(D)≥λQ(D′)=

2n-m+1>2n-m.

当k=3且n3≥5时，设u和v是Kn1中不同的两个点.在QD(G)中取2×2阶主子矩阵:

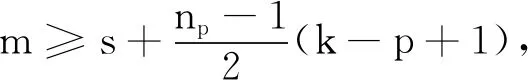
进而有

TrG(v)=TrG(u)=

s+n1-1+2(n-s-n1)≥2n-m.

令

由引理4与引理5，得

λQ(G)≥λQ(E)≥λQ(E′)=2n-m+1>2n-m.

综上所述，当G≅Ks∨(Kn1∪Kn2∪…∪Knk)时，λQ(G)>2n-m.当GKs∨(Kn1∪Kn2∪…∪Knk)时，由引理1可知，

λQ(G)>λQ(Ks∨(Kn1∪Kn2∪…∪Knk))，

进而有λQ(G)>2n-m．

情况2t>k．

此时，G-X0不仅有k个奇连通分支，且有t-k个偶连通分支.将图G的每一个偶连通分支Hj(k+1≤j≤t)中的某个点，与奇连通分支H1中的某个点连接一条边后得到的图记作G′.

显然G′-X0也有k个奇连通分支，且图G′的最大匹配数m(G′)≥m.由引理6，有

n-2m≥n-2m(G′)≥o(G′-X0)-|X0|=

o(G-X0)-|X0|=n-2m.