交换环的素谱与极大谱的连通性
谢国根
(铜陵学院数学与计算机学院,安徽 铜陵 244000)
交换环的素谱与极大谱的连通性
谢国根
(铜陵学院数学与计算机学院,安徽 铜陵 244000)
试图刻划交换环的素谱和极大谱的连通分支,为此本文讨论了交换环的本原幂等元与素谱以及极大谱的连通分支的关系.证明了若e为本原幂等元,则D(e)为SpecA的连通分支.类似地,若e为A的本原幂等元且Nil(A)=Rad(A),则为maxA的连通分支.
素谱;极大谱;连通性;本原幂等元
1 引言
交换环的素谱和极大谱是代数几何的重要研究对象之一,已知交换环A的素谱是连通的当且仅当A中只有0和1是幂等元.由于对任意拓扑空间,它的连通分支构成它的覆盖.所以若交换环的素谱不连通,可以进一步去研究它的连通分支.因此不同于文献[1-3]讨论素谱整体的的连通性,本文主要研究其连通分支,首先讨论了素谱的连通分支与交换环的本原幂等元的关系,并随后讨论了极大谱上的相应情形.
2 拓扑上的预备知识
定义 2.1称映射f:X→ Y是连续的(X,Y为拓扑空间),若Y的任意一开集的原像是X的开集,或等价地,Y的任意一闭集的原像是X的闭集.
定义 2.2拓扑空间X称为连通的,如果它不能分解为两个非空不相交开集的并(或者等价地,它不能分解为两个非空不相交闭集的并).
引理 2.1连通空间在连续映射下的像也是连通的.
定义 2.3拓扑空间X的一个子集称为X的连通分支,如果它是连通的,并且不是X的其他连通子集的真子集.
引理 2.2X的每个非空连通子集包含在唯一的一个连通分支中.
注 2.1X中任意一点x作为子空间是连通的,因此x包含在唯一的连通分支中.换句话说,X的所有连通分支构成X的覆盖,并且它们两两不相交.
引理 2.3连通分支是闭集.
3 素谱的连通分支与本原幂等元的关系
注 3.1若A为交换环,记SpecA为A的所有素理想的集合.记V(a)={p∈SpecA|a⊂p}.对任意f∈A,(f)表示fA,记

则SpecA以V(a)为闭子集构成拓扑空间.
引理 3.1令A是交换环,则下列条件等价:
(i)SpecA是连通的.
(ii)A中只有0和1是幂等元.
证明见文献[5]命题1.3.1.
注 3.2由文献[5]命题1.3.1的证明过程可知,对任意A中的幂等元e,

引理 3.2设 e为交换环 A的幂等元,做环同态 ϕ:A→ Ae使得 ϕ(r)=re,r∈A,则f:SpecAe→SpecA(其中f(q)=ϕ−1(q),q∈SpecAe)连续,且Im f=D(e).
证明f的连续性可由文献[5]中的命题1.2.5得到,下证Im f=D(e).
对任意 q∈SpecAe,由 q是素理想,e是 Ae的单位元可知,e/∈q,所以 e/∈ϕ−1(q),即Im f⊂D(e).
反之,对p∈SpecA且e/∈p,由V((e))∪V((1−e))=SpecA知,(1−e)⊂p,所以

显然,p∩(e)为Ae的素理想.
易得ϕ−1(p∩(e))⊃p,且若x∈ϕ−1(p∩(e)),即xe∈p∩(e).又x=xe+x(1−e),所以

故ϕ−1(p∩(e))=p,即Im f⊃D(e).
定理 3.1设e为交换环A的本原幂等元,则D(e)为SpecA的连通分支.
证明因为e为交换环A的本原幂等元,所以Ae中的幂等元只有0和e.由引理3.1知SpecAe是连通的.则由引理3.2知D(e)为连通空间SpecAe在连续映射下的像,则由引理2.1知D(e)为SpecA的连通子集.
由引理2.2,可设F是包含D(e)的连通分支,且由引理2.3知,F是闭集.再由引理3.1的注记知D(e)=V((1−e)),故D(e)也是闭集.由D(e)⊂F得,
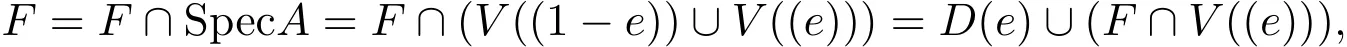
且D(e)∩(F∩V((e)))=∅,由F的连通性知F∩V((e))=∅,即F=D(e).
所以D(e)是SpecA的连通分支.
由文献[6]中第7节的练习7,练习8可得到如下引理:
引理 3.3设R是由一切连续函数f:构成的环.则R的每个幂等元都不是本原的.
注 3.3由引理3.3知,对任意交换环A,SpecA的连通分支未必能写成D(e)的形式(其中e是A的本原幂等元).所以定理3.1的逆命题不成立.
4 极大谱的连通分支与本原幂等元的关系
一些记号及说明若A为交换环,记maxA为A的所有极大理想的集合.记A的所有素理想的交为Nil(A),记A的所有极大理想的交为Rad(A).
易得:
(2)如果{ai}(i∈A)是A的理想的任意集合,则
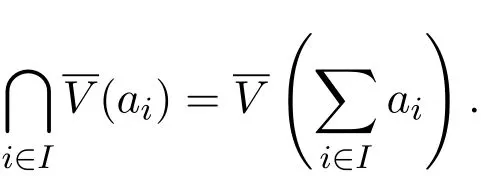
(3)如果a,b是A的两个理想,则

对任意f∈A,(f)表示fA,记
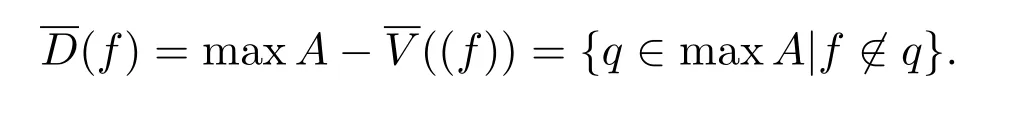
引理 4.1设a是交换环A的诣零理想,=A/a.则若x∈A使得是的幂等元,则存在A的幂等元e,使得
证明见文献[8]定理1.8.5.
引理 4.2令A是交换环,且Nil(A)=Rad(A),则下列条件等价:
(i)maxA是连通的.
(ii)A中只有0和1是幂等元.
证明(i)⇒(ii)设e为A的幂等元,则e(1−e)=0.所以


因此a,b为A的真理想,且

注 4.1由希尔伯特零点定理 (文献 [9]定理 1.6)可知,若 A为有限生成 K 代数,则Nil(A)=Rad(A),所以这里要求Nil(A)=Rad(A)并不是一个相当苛刻的条件.有限生成K代数在代数几何中是一类相当重要的环.
引理 4.3若ϕ:A→B为交换环A,B的满同态,则对任意q∈maxB,有ϕ−1(q)∈maxA,且由此诱导的映射f:maxB→maxA(其中f(q)=ϕ−1(q))连续.
证明由于是ϕ满同态,所以在A中包含kerϕ的理想和B中的理想一一保序对应.因此ϕ−1(q)∈maxA.
再由对任意A的理想a,及q∈maxB,
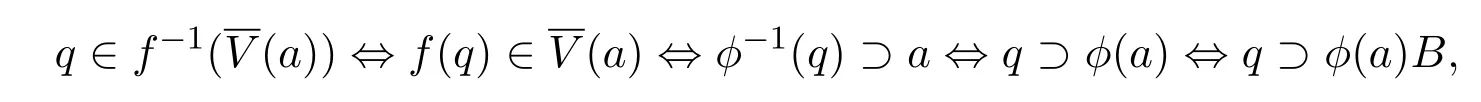
引理 4.4设 e为交换环A的幂等元,做环同态 ϕ:A→Ae使得ϕ(r)=re,r∈A,
则f:maxAe→maxA(其中f(q)=ϕ−1(q),q∈maxAe)连续,且Im
证明f的连续性可由引理4.3得到,下证
仅需证明

余下的证明与引理3.2类似.
再由ϕ是满同态,所以A中包含kerϕ的理想和Ae中的理想一一保序对应.因此
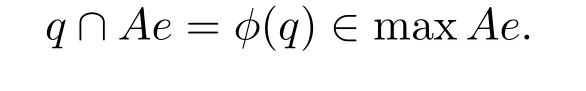
定理 4.1设e为交换环A的本原幂等元,且Nil(A)=Rad(A),则(e)为maxA的连通分支.
证明仅需说明Nil(A)=Rad(A)⇒Nil(Ae)=Rad(Ae),余下证明与定理3.1类似.
由引理 4.4的证明过程可知 q∈maxA,e/∈q⇒ q∩Ae∈maxAe.另外显然有 q∈maxA,e∈q⇒Ae⊂q.所以对于任意x∈Ae,若x∈Rad(Ae),则有x∈Rad(A)=Nil(A).故x幂零.因此x∈Nil(Ae),即Nil(Ae)=Rad(Ae).
5 总结
本文主要是利用本原幂等元来刻画素谱和极大谱的连通分支,但是由引理3.3知,并不是所有的连通分支都可以用本原幂等元来刻画.所以认为有以下问题是值得进一步研究的:
(1)能否给出素谱和极大谱的连通分支的一般形式的刻画;
(2)如(1)不能实现,那么能否对一些特殊的环(如引理3.3中提到的环)刻画出它所有的连通分支.
[1]冯良贵.环的素谱的若干注记(英文)[J].数学研究,2001(1):27-30.
[2]王江.交换环的素谱空间的连通性[J].山东师大学报:自然科学版,1989(2):16-22.
[3]陈刚.一个特征标环素谱的连通性[J].数学杂志,2005(2):30-34.
[4]高恩伟,张金霞.素理想P在F中分解[J].纯粹数学与应用数学,2012(5):569-572.
[5]Fu L.Algebraic Geometry[M].北京:清华大学出版社,2006.
[6]Anderson F W,Fuller K R.Rings and Categories of Modules[M].New York:Spring-verlag,1974.
[7]尤承业.基础拓扑学[M].北京:北京大学出版社,1997.
[8]王芳贵.交换环与星形算子理论[M].北京:科学出版社,2006.
[9]Iitaka S.Algebraic Geometry:An Introduction to Birational Geometry of Algebraic Varieties[M].New York: Spring-Verlag,1982.
Connectedness of the prime spectrum and the maximal spectrum of a commutative ring
Xie Guogen
(College of Mathematics and Computer,Tongling University,Tongling 244000,China)
The main purpose of this paper is trying to character connected components of the prime spectrum and the maximal spectrum of a commutative ring.To this aim,the relationship between primitive idempotents and connected components of the prime spectrum and the maximal spectrum is discussed.It is proved that D(e)is a connected component of SpecA if e is a primitive idempotent of A.Analogously,(e)is a connected component of maxA if e is a primitive idempotent of A and Nil(A)=Rad(A)
prime spectrum,maximal spectrum,connectedness,primitive idempotent
O178
A
1008-5513(2014)02-0216-05
10.3969/j.issn.1008-5513.2014.02.014
2013-06-09.
谢国根(1985-),硕士生,研究方向:环论与代数表示论.
2010 MSC:16D10

