半群PODn的反保序平方幂等元

黄新旭，游泰杰

(贵州师范大学 数学与计算机科学学院,贵州 贵阳　550001)



半群PODn的反保序平方幂等元

黄新旭，游泰杰

(贵州师范大学 数学与计算机科学学院,贵州 贵阳550001)

摘要：设PODn是Xn上的保序或反保序部分变换半群。对n≥4, 证明了半群PODn秩为n-1的元素为反保序平方幂等元的充分必要条件。

关键词：保序或反保序部分变换半群; 反保序平方幂等元; 充分必要条件

0引言

设自然数n≥4, Xn={1,2,…,n}并赋予自然序,PTn是Xn上的部分变换半群。设α∈PTn, 若对任意的x,y∈dom(α),x≤y⟹xα≤yα, 则称α是保序的。设POn为PTn中的所有保序部分变换之集, 则POn是PTn的子半群, 称POn为保序部分变换半群。反之, 若对任意的x,y∈dom(α),x≤y⟹xα≥yα, 则称α是反保序的, 设PDn为PTn中的所有反保序部分变换之集。令PODn=POn∪PDn, 易验证PODn是PTn的子半群, 称PODn为保序或反保序部分变换半群。根据PODn的性质可知, 任意两个保序变换或任意两个反保序变换的乘积是保序变换, 而保序变换与反保序变换的乘积是反保序变换。

设α∈PTn, 若α2=α, 则称α是一个幂等元。 若α2=α4(α2是幂等元), 则称α是一个平方幂等元; 若α既是反保序的又是平方幂等元, 则称α是一个反保序平方幂等元。 平方幂等元的概念是Umar在文献[1]中首次提出。 接着在1999年, 文献[2]研究了有限变换半群的平方幂等元。 2001年, 文献[3]研究了保序链的有限变换半群中的平方幂等元。 2013年, 文献[4]研究了有限变换半群中由平方幂等元生成的子半群。 2014年, 文献[5]研究了保序变换半群的顶端的平方幂等元的充要条件。而最近一篇关于研究平方幂等元的文章则是在2015年发表的文献[6], 它研究了保序部分变换半群的顶端的平方幂等元的充要条件。 由此可见, 目前对平方幂等元进行研究的文章并不多。 本文类比平方幂等元的概念, 提出反保序平方幂等元的概念, 并证明了半群PODn秩为n-1的元素为反保序平方幂等元的充分必要条件。

本文未定义的术语及符号请参见文献[7]。

1准备知识

据文献[8]的结果, PODn中的Green关系有如下刻画:

(α,β)∈L⟺im(α)=im(β),

(α,β)∈R⟺ker(α)=ker(β),

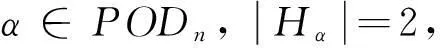
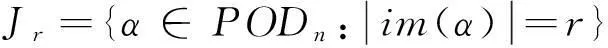
下面我们考虑PODn的J-类Jn-1:

1)Jn-1=[n,n-1]∪[n-1,n-1]。

2)Jn-1中共有n个L-类，记为L(1),L(2),…,L(n), 其中

2主要结果

定义1设i∈Xn,α∈PODn,若i∈dom(α), 有iα∈dom(α), 并且存在j∈dom(α),使得iα=j,jα=i, 则称i为α的可成对量, 并称i与j成对, 同理j与i成对。 用Twin(α)表示α的所有可成对量组成的集合。

定义2设i∈Xn,α∈PODn, 若i∈dom(α), 有iα=i, 则称i为α的固定点。 用Fix(α)表示α的所有固定点组成的集合。 注意到每个固定点都与自身成对, 即Fix(α)⊆Twin(α)。

定理1设n≥4, α为Jn-1中的反保序变换, 则

1)当α∈[n,n-1], A为α的非单点核类, 若A⊄im(α), 那么α为反保序平方幂等元的充分必要条件是

dom(α)∩im(α)=Twin(α)。

2)当α∈[n,n-1], A为α的非单点核类, 若A⊆im(α), 那么α为反保序平方幂等元的充分必要条件是

dom(α)∩im(α)=Twin(α)∪A。

3)当α∈[n-1,n-1], α为反保序平方幂等元的充分必要条件是

dom(α)∩im(α)=Twin(α)。

证明1) 充分性设dom(α)∩im(α)=Twin(α), 于是dom(α2)=(dom(α)∩im(α))α-1=Twin(α)α-1,

易验证im(α2)=Twin(α),

注意到α为反保序变换, 从而α2为保序变换。 因此对任意的t∈im(α2), 有t∈t(α2)-1。 所以α2是幂等元, 故α是反保序平方幂等元。

2)充分性设dom(α)∩im(α)=Twin(α)∪A,

于是dom(α2)=(dom(α)∩im(α))α-1=(Twin(α)∪A)α-1=Twin(α)α-1∪Aα-1,

易验证im(α2)=Twin(α),

注意到α为反保序变换, 从而α2为保序变换。 因此对任意的t∈im(α2), 有t∈t(α2)-1。 所以α2是幂等元, 故α是反保序平方幂等元。

必要性 显然Twin(α)∪A⊆dom(α)∩im(α),下面只需证明dom(α)∩im(α)⊆Twin(α)∪A。 运用反证法。 设dom(α)∩im(α)⊄Twin(α)∪A, 由于dom(α)∩im(α)=im(α),于是im(α)⊄Twin(α)∪A,假设任意的x∈im(α)(Twin(α)∪A),都有x∈x(α2)-1与α∈Jn-1矛盾。 从而存在x∈im(α)(Twin(α)∪A),使得x∉x(α2)-1,与α2是幂等元矛盾。 因此dom(α)∩im(α)⊆Twin(α)∪A, 综上dom(α)∩im(α)=Twin(α)∪A。

3)充分性设dom(α)∩im(α)=Twin(α), 于是

dom(α2)=(dom(α)∩im(α))α-1=Twin(α)α-1=Twin(α),

从而 dom(α2)α2=Twin(α)α2=Fix(α2),

因此α2是幂等元, 故α是反保序平方幂等元。

参考文献：

[1] UMAR A.On the semigroup of partial one-one order-decreasing finite transformation[J].Proc Roy Soc Edinburgh，123A 1993：355-363.

[2] MADU B A.Quasi-idempotents and quasi-nilpotents in finite transformations semi-groups[D/OL].Nigeria:Ahmadu Bello University Zaria,1999.

[3] MADU B A,GARBA G U.Quasi-idempotents in finite semigroups of order-preserving charts[J].Research Journal of Science，2001(7)：61-64.

[4] IMAM A T.Subsemigroups generated by quasi-idempotents in certain finite semi-groups of mappings[D/OL].Nigeria:Ahmadu Bello University Zaria,2013.

[5] 李红香,游泰杰,赵平.保序变换半群On的平方幂等元[J].贵州师范大学学报(自然科学版),2014,32(1): 48-50.

[6] 吴江燕,游泰杰.保序部分变换半群POn的平方幂等元[J].东北师大学学报(自然科学版),2015, 47(3): 6-11.

[7] HOWIE J M.An introduction to semigroup theory[M].London:Academic Press，1976.

[8] FERNANDES V H,GOMES G M S，JESUS M M.Congruences on monoids of order-preserving or order-reversing transformations on a finite chain[J].Glasgow Math J，2005(47)：413-424.

文章编号：1004—5570(2016)01-0052-03

收稿日期：2015-08-25

作者简介：黄新旭(1990-), 女, 在读硕士研究生, 研究方向: 半群代数理论, E-mail: 513991995@qq.com.

中图分类号：O152.7

文献标识码：A

The order-reversing quasi-idempotent of the semigroup PODn

HUANG Xinxu, YOU Taijie

(School of Mathematics and Computer Science, GuiZhou Normal University, Guiyang, Guizhou 550001, China)

Abstract:Let PODn be the order-preserving or order-reversing partial transformations semigroup on Xn.when n≥4， we showed that the necessary and sufficient conditions of the element of rank n-1 of the semigroup PODn is order-reversing quasi-idempotent.

Key words:order-preserving or order-reversing partial transformations semigroup; order-reversing quasi-idempotent;necessary and sufficient conditions