基于Leslie矩阵的水资源供需平衡灰色预测研究

刘　帅，袁汝华

(河海大学 商学院，江苏南京　211100)



基于Leslie矩阵的水资源供需平衡灰色预测研究

刘帅，袁汝华*

(河海大学 商学院，江苏南京211100)

摘要：探索区域水资源供需平衡是生态环境保护的重要前提。选取影响水资源供需平衡的12个指标，采用Leslie转移矩阵模型对定量指标进行测算，并运用灰色预测模型对不确定性指标因素进行灰度预测。通过对南京市雨花台区的水资源供需进行实证分析，结果表明：该合成模型预测效果比传统Leslie矩阵和灰色预测效果好，拟合精度最高，预测精度有效的控制在5%之内。该模型拓宽了灰色预测模型在水资源供需平衡中的应用，对水资源的科学预测具有一定的意义。

关键词：水资源；供需平衡；灰色系统；Leslie矩阵

进行水资源的供需分析，揭示供需之间的矛盾，预测未来可能发生的问题，可以未雨绸缪，使区域内的水资源能更好地为国民经济、人民生活服务，为人类生存创造更为良好的环境[1]。影响水资源供需平衡的主要因素为不同水平年需水量和可利用水量，且水资源供需平衡随着时间的推移是一个逐渐发展的过程[2]。目前国内外学者对于区域内水资源供需平衡预测的方法进行了深入的研究[1-4]。已有文献所用的预测方法主要有时间序列分析法[3-5]、神经网络[6-8]、灰色预测[9-12]。其中灰色预测模型是一种比较成熟的方法，但是灰色预测模型也存在一些不足，它只适用于呈近似指数增长规律的数据序列，而且求解参数的算法也有一些缺陷。而Leslie矩阵构建的平衡动力学方程，利用某一初始时刻水资源供需结构特点，可以动态的预测区域供给量结构及需求量随时间的演变过程。

采用基于Leslie矩阵模型与灰色系统理论的合成模型，即改进的Leslie矩阵灰色预测模型来确定行区域内水资源供需平衡预测。该方法能从水资源供需的影响因素出发，既发挥了Leslie矩阵预测模型在定量分析中的客观性，又突出了灰色系统在工业化水平和居民生活水平不断提高条件下，影响水资源供需在不确定因素条件下的预测能力。选取南京市雨花台区水资源供需情况进行实证分析，以期验证该模型水资源供需预测的可信度和精确度。

1水资源供需平衡影响因素分析

以2010年为基准年，2015年为近期水平年，2020年为中期水平年，2025年为远期水平年。根据相关规范要求，地区内近期工业用水保证率95%，农业用水保证率达75%，生态用水初步保障；中期工业用水保证率95%，不考虑传统农业用水，仅经济作物用水得到保障和生态用水得到基本保障；远期工业用水保证率达95%，同时考虑经济作物用水得到保障和生态用水的得到保障。

由水资源供需平衡方程可知，影响供需变化不外乎需水总量和可利用水量两大因素[13]。为了综合考虑影响水资源的因素对供需平衡的作用论，以及客观上受传统经验数据的全面性制约，因此，假设没有也不可能包含影响供需平衡的全部变量。如果所缺失的变量在估计的时间范围内基本保持不变，则可以将其影响归入到不确定性因素中，其中，不确定性因素主要包括经济因素和政策因素等。

1.1需水总量

不同保证率需水量是指在某种生产条件下，遇到不同频率的雨情、水情、旱情，各用水部门需求的水量。需水量主要包括生产生活用水、生态用水和公共事业用水。

1.1.1生产生活用水量

生产生活用水主要包括工业用水、农业用水和生活用水。工业用水量常见的计算方法有相关分析法、弹性系数法和重复利用率提高法。采用通用的万元产值法计算工业用水量。根据南京市雨花台区统计资料现实，工业平均年增产率为10%，工业万元产值用水量为65m3/万元，考虑采取节水技术措施，预测近期、中期和远期的万元产值用水量分别为45m3/万元，35m3/万元和25m3/万元。农业用水量主要考虑灌溉用水，采用灌溉定额预测方法进行计算。以农业人口及城镇人口生活用水定额分为100L/(d·人)、180L/(d·人)，对生活用水量采用定额法进行预测，预测2015年、2020年和2025年城镇人口生活用水定额分别是210L/(d·人)、230L/(d·人)和250L/(d·人)。人口发展趋势除了要考虑人口的自然增长，还应该考虑工业化水平和房地产开发导致的大量外来人口的迁入。

1.1.2生态用水量

生态用水量主要包括河道生态用水量、绿地生态用水量和改善水环境的引水量。河道在城市生态系统中发挥着重要作用，适宜的河道水量促进城市生态系统水量、水质、水温及水热等各种平衡。河流生态用水量可按照河段分别计算维持河流生态系统供需平衡的水源涵养林用水量、水热平衡用水量、水沙平衡用水量、水位平衡用水量和水量平衡用水量5个方面；绿地生态用水量采用定额计算法，规划近期、中期和远期的绿化率以及用水定额量；改善水资源用水量主要是为了改善水环境，根据各主要河道目前的污染物浓度，以及近远期目标浓度要求，计算出各主要河道的年引水量。

1.1.3公共事业用水量

城市公共事业用水一般包括社会服务用水、教育事业用水、行政事业用水、经营服务用水、特种用水等方面的用水量。目前全国公共事业用水定额为80L/(d·人)。考虑到社会服务系统逐步完善、教育事业发展等方面的因素，公共事业用水定额有增大的趋势，根据Logistic线性回归预测，可得2015年、2020年和2025年公共事业用水定额分别为120L/(d·人)、135L/(d·人)和150L/(d·人)。

1.2可利用水资源

我国的地下水资源虽然丰富，但是目前已经到了开采需要严格控制的局面。2013年6月实施的《我国水资源保护条例》对地下水资源开采作出了明确的规定，严格控制地下水开采。虽然河流区域在取水方面有优势，而地下水开采将带来地面沉降等不利影响，因此，可供水量不考虑地下水资源，供水途径主要由降雨径流可利用量、水厂供水、工业重复用水量、农业回归水量组成。

降水径流可利用量是指在区域水资源未被任何利用的情况下，在地表产生的地表径流量。可利用年降水径流关系，通过降水量资料推求区域径流量，考虑保证率50%、75%、95%下的径流可利用系数分别为0.35、0.45和0.55；我国区域内河流水量丰富、水体自净能力强，虽然存在多处岸边污染带，但是主流水质好为地区提供了良好的水源条件。目前地区的供水厂主要是企业自备水厂。根据全国“十五”节水规划，工业用水重复率为40%，参照工业用水重复率的增长状况，预期2015年，2020年和2025年工业用水重复率为50%、53%和55%。农业回归水量的取用水保证率为50%、75%、95%，回归系数分别为0.43、0.45、0.47。

1.3不确定性因素

区域内水资源供需平衡受诸多不确定性因素影响。为更准确地对区域内水资源供给平衡进行研究，研究将一切不确定性因素纳入模型考虑。工业发展因素对水资源平衡的作用主要表现在它决定了水需求量的增值条件，通过改变工业用水可循环和不可循环更多地影响着水资源供需平衡。随着经济水平的提高，工业用水增长率趋于下降，现代社会里这一趋势尤为明显，水资源的经济效应主要通过作为生产者和消费者的统一而体现出来[2]。其中，地区差异包含地域工业水平差异带来的经济政策的不同。因此，不确定性因素对水资源供需平衡预测具有不可缺少的影响。综上，水资源供需平衡影响因素体系考虑以下因素，如图1所示。

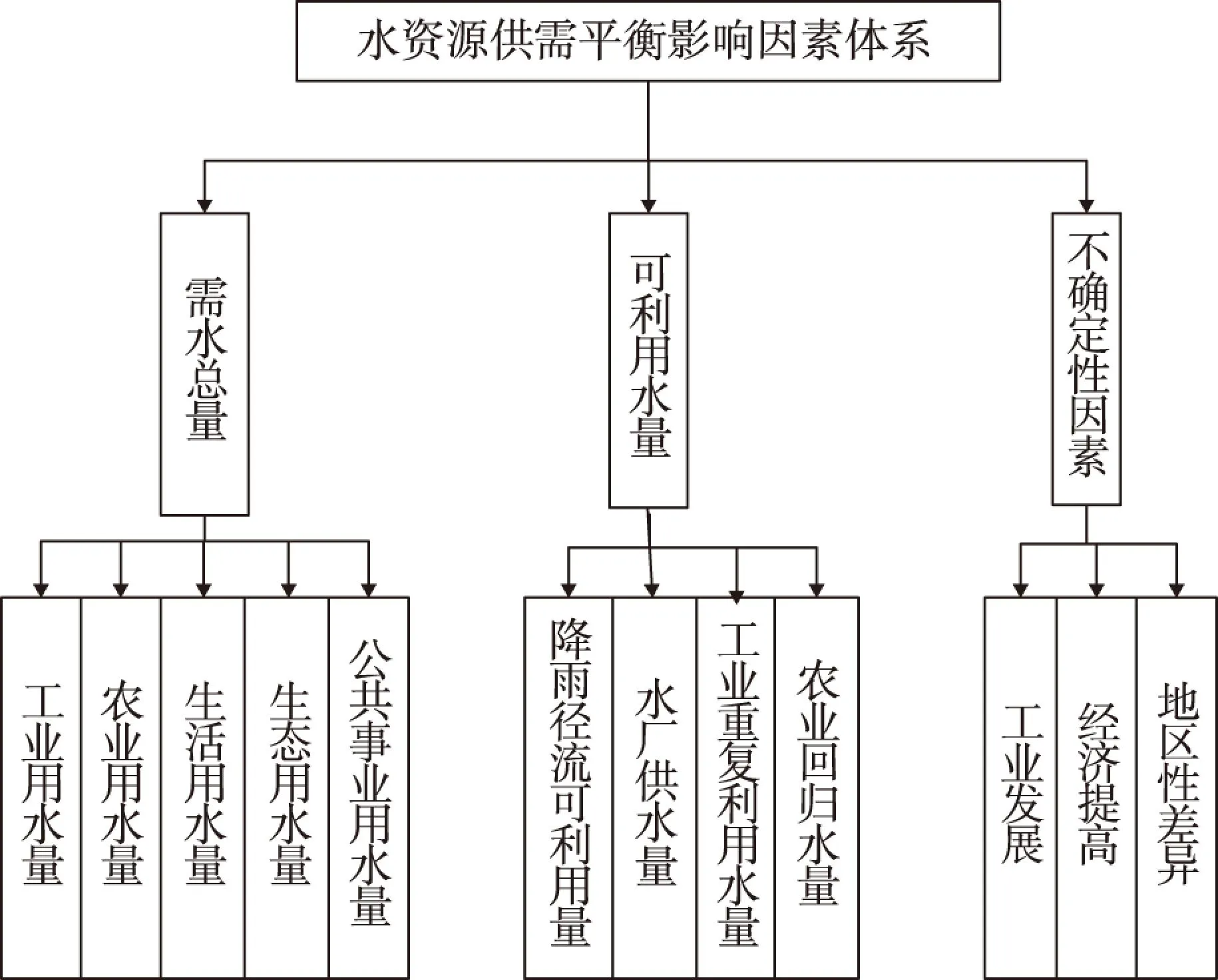
图1　水资源供需平衡影响因素体系Fig.1　Index system of balance of supply and demand of water resources

2改进的Leslie矩阵灰色预测模型

2.1灰色GM(1,1)模型基本原理

灰色系统理论将所有的系统划分为白色、黑色和灰色系统[14]。所谓“白”就是指所有信息已知；“黑”就是指所有信息未知；“灰”就是指部分信息已知，部分信息未知。供需平衡预测模型就是典型的灰色系统，对其影响的地区经济、生态环境、政策影响等情况是已知的，但是其他一些影响因素，例如自然灾害、心理影响等是难以确切的。灰色理论的特点在于其对不确定性因素进行灰色、灰过程的处理上，即用“生成”的方法对原始数据进行处理，得到随机性弱化，规律性增强的新数列进行建模。灰色预测模型的特点在于所需负荷数据少，不需要计算统计特征值，建模精度高。因此，在各种预测领域，特别是不确定性明显和数据较少的领域中得到较多的应用。

灰色GM(1,1)能够有效控制水资源供需量不确定因素的变化。引进控制变量时，可由灰色GM(1,1)理论引进控制变量序列Ii(t)，则模型的首要在于一次累加生成，记为Ii(0)→Ii(1)，即：Ii(1)=[Ii(1),Ii(2),…,Ii(n)]，其中，然后构造控制变量的向量Xn与矩阵A。

Xn=(Ii(2),Ii(3),…,Ii(n))T

运用最小二乘法求解系数μ，a=(ATA)-1BTXn。则GM(1,1)模型进行灰色预测：

(1)

式(1)中，I0(k)为预测值，Ii(k)的i为迭代次数，a为变化系数，k为年份叠加变化量，u为灰色G(1,1)的灰作用变化量系数。

2.2Leslie矩阵模型基本原理

水资源供需变化除受到供给量和需求量影响，还受到其他诸多因素影响[15]。对水资源供需平衡趋势分析，需要考虑到未来对水资源需求量不同，经济差异和工业结构特征等诸多因素的共同影响，这使得基于传统的分析方法对水资源供需平衡变化特征的有效性存在明显缺陷。利用Leslie矩阵水资源供需平衡预测模型可分析不同年份供需总量的变化，从而预测地域内未来的供需量以及供需平衡问题。

由于水资源的供需通常按照时间规律有一定比例，则本研究中，时间以年为单位，设最大需求量为nm3，yi(t)为t年i供需平衡率的水资源总量，i=0,1,…,n.t=2010,…,2025。只考虑由于水资源供给量和需求量引起的水资源供需平衡变化，不计其他因素影响，记bi(t)为t年i取水保证率，则有：yi+1(t+1)=(1-bi(t))yi(t)，其中i=0,1,…,n-1.t=2010,…,2025，。另记ci(t)为t年i供需平衡量，di(t)为t年i引水量，则水资源供需平衡预测模型为：

(2)

2.3改进Leslie矩阵灰色预测模型

在水资源供需平衡动态预测模型中，需要考虑地区内的工业化水平不断提高、人民生活水平不断提升和工农业用水量不断的增加等因素。因此，要实现对供需平衡的科学预测，需要考虑到上述不确定因素的影响。研究利用灰色GM(1,1)作为不确定因素的灰色估计，再结合Leslie矩阵预测模型，进而改善对水资源供需平衡做出科学的预测模型。由灰色GM(1,1)引进的控制变量Ii(t)，使得bi(t)=α(t)Ii(t)，其中，α(t)是控制供需量的主要参数，称为综合供需率，其表示t年水资源循环利用率。

在现实环境下，可得bi(t)、Ii(t)、di(t)、c(t)与时间t无关，则bi(t)=bi,Ii(t)=bi,Ii(t)=Ii,di(t)=di,c(t)=c，即改进的Leslie矩阵的水资源供需平衡预测模型为：

(3)

3水资源供需平衡预测实证分析

收集南京市统计年鉴关于水资源的数据，综合考虑水资源供给量和需求量的定量指标，以2005～2014年供给量和需求量随年份变化量数据作为拟合函数的基础，绘制水资源供给量和需求量曲线，如图2所示。

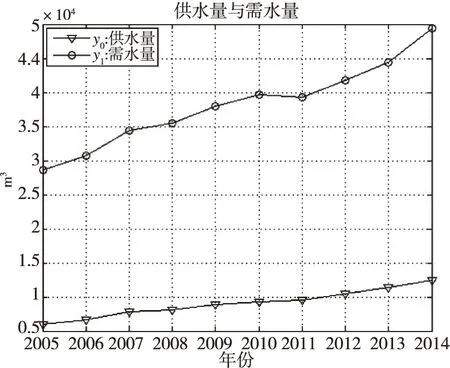
图2　2005～2014年雨花台区水资源供需量Fig.2　Balance of supply and demand for water resources of Yuhuatai in 2005～2014

由图2的水量平衡拟合所示，南京市雨花台区可利用水量(降水径流可利用量、农业回归量、工业回归水量)不能满足需水要求，每年都需要大量引取长江水。从供需平衡图中的数值差额，还可以看出供水缺口正逐年加大。如果南京市雨花台区水资源不能得到保证，那么地区供水将面临危机。供水量和需水量的变化对水资源供需平衡的变化是显著的，因此，将工业与生活用水需求量的变化等不确定性因素纳入供需平衡预测模型是非常必要的。

对南京市雨花台区供水量和需水量预测进行分析时，为准确预测供水量、需水量和引水量三者对水资源供需平衡的影响，以2010年为基准年，2015年为近期水平年，2020年的中期水平年和2025年的远期水平年，通过研究1959～2009年的历史水资源供需数量值作为原始数据，并结合Leslie矩阵灰色预测合成模型，对基准年与不同水平年在不同的保证率条件下进行数值预测。其中，利用中心差分的方法对公式(1)进行数值差分，利用向前差分的方法对公式(2)、(3)进行数值差分，最后运用Matlab软件进行计算。结果如表1所示。

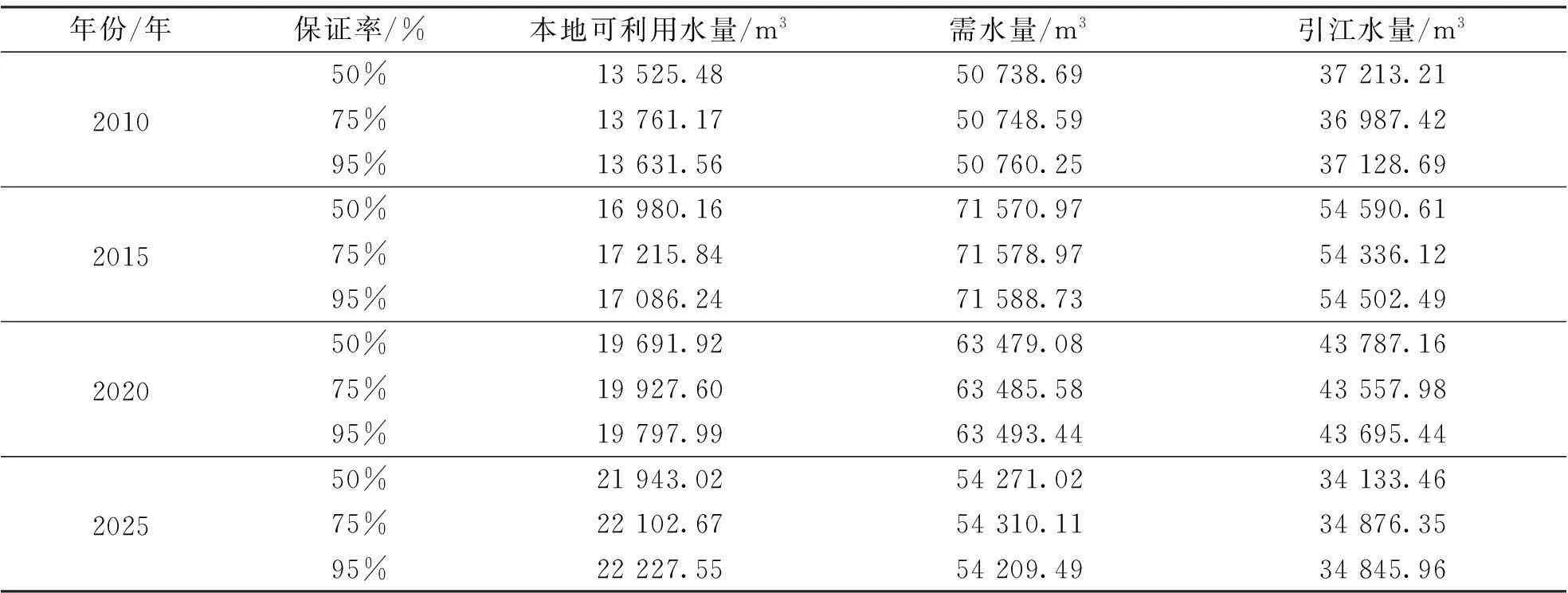
表1　雨花台区水资源供需平衡预测分析表

通过将定量数据引入Leslie矩阵预测模型中，再将不确定性因素考虑到灰色预测中，以2010年南京市雨花台区本地可利用水量、需水量和引降水量作为拟合检验的基础，与50%保证率下改进的Leslie矩阵灰色预测模型的仿真数值进行比较，并将计算所得预测值与灰色预测模型和Leslie矩阵灰色预测模型的预测值进行拟合检验，结果如表2所示。

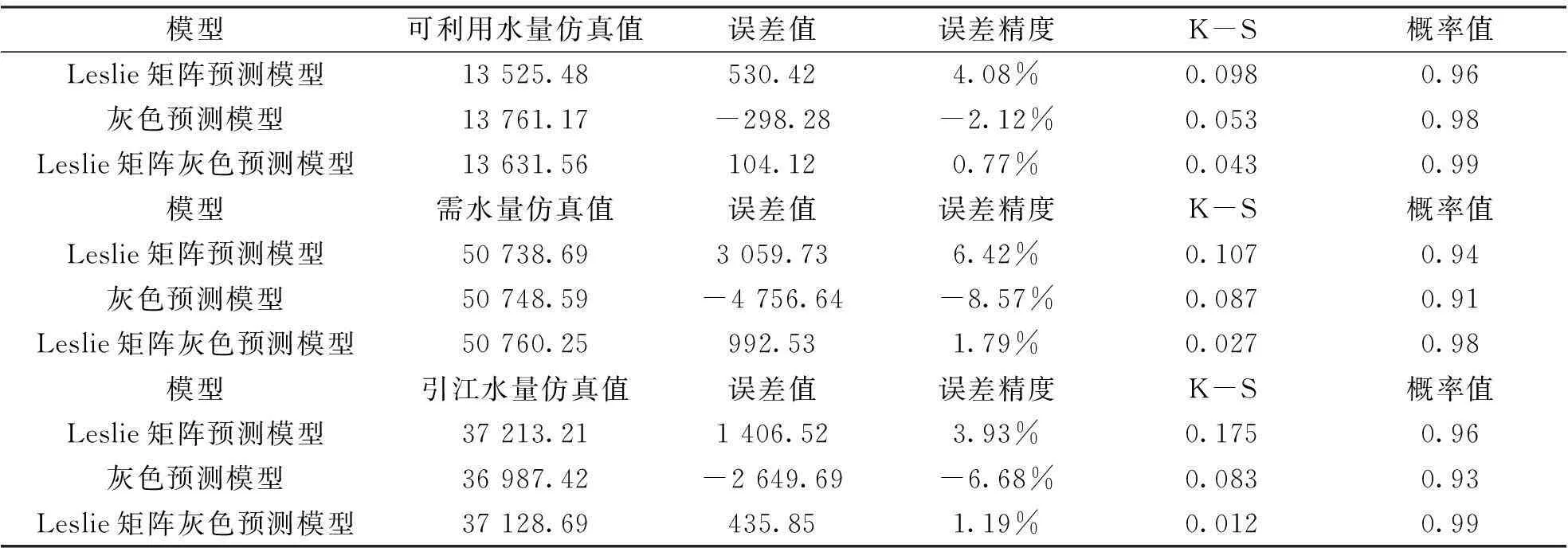
表2　Leslie矩阵灰色预测模型与其他模型拟合检验

注：概率值为分布模型准确性检验的概率值。

从表2可见，除了灰色预测模型，其余两种模型预测误差值均为正数，且Leslie矩阵灰色预测模型在计算可利用水量、需水量和引江水量的误差精度比Leslie矩阵预测模型的误差精度分别提高了3.31%、4.36%和2.74%。从K-S拟合概率角度看，Leslie矩阵灰色预测模型的实测值与预测值比灰色预测模型的两分布的差异率分别提高了1.0%，6.0%和7.1%，数据的拟合概率相对最高。由此，可以认为Leslie矩阵灰色预测模型比其他两种模型更能准确地描述水资源平衡变化特征。同时，Leslie矩阵预测模型拟合程度较低，可认为存在一定的拟合偏差。在短时间水资源供需平衡结构不变，即供水量和需水量不变的情况下，改进Leslie矩阵灰色预测模型所预测的结果的误差率均有效控制在5%以内，精确度最高。因此，利用改进Leslie矩阵灰色预测模型对水资源供需平衡预测具有可行性和有效性。

4结论与讨论

利用传统Leslie矩阵对影响水资源平衡的定量数据进行迭代计算，然后运用灰色矩阵将影响水资源平衡的不确定性因素数据化并纳入迭代计算中，改进Leslie矩阵灰色预测模型。选取南京市雨花台区的水资源供需情况进行验证分析，检验该合成模型，并与传统的Leslie矩阵预测模型和灰色预测模型进行比较。结果表明：在对“可利用水量、需水量和引江水量”数值仿真上，Leslie矩阵预测模型的整体预测结果偏大，且误差率均值为4.81%；灰色预测模型的预测结果整体偏小，且误差率均值为-5.79%；而改进Leslie矩阵灰色预测模型预测值居于两模型结果之间，误差率均值为1.25%，K-S拟合检验差异率均在2%以内，两分布波幅小且精确度最高。

传统Leslie矩阵预测模型所得预测序列趋势发展稳定，预测结果较为保守，对于水资源供需平衡趋势稳定的区域，预测效果良好，但不适应水资源供需在不确定性因素条件下的预测；而灰色预测模型在预测过程中，可以考虑到不确定因素的影响，但对水资源供需的定量仿真中出现数值偏小的估计。因此，选择改进Leslie矩阵灰色预测模型可克服了灰色预测模型的主观随意性较大的缺陷，又发挥了Leslie矩阵预测模型的客观性。在可预见的范围内，将不确定性的影响变量转化为灰色预测，并加入Leslie矩阵预测模型中，得到的预测值更加接近实际情况，该合成模型对水资源供需平衡趋势可做出更可靠的估计。

参考文献：

[1] 中国农业百科全书编委会.中国农业百科全书·水利卷(下)[M].北京:农业出版社,1986:777-779.

[2] 李兴东,武耀华.基于ARIMA的民勤绿洲水资源承载值时间序列预测[J].兰州交通大学学报，2012,31(3):177-181.

[3] 袁树堂,刘新有,王红鹰.基于区域发展规划的崇明县水资源供需平衡预测[J].水资源与水工程学报，2014,25(6):76-81.

[4] 李博,郭小铭,徐爽,等.基于灰色关联分析法的织金县比那泉水质评价[J].贵州师范大学学报(自然科学版)，2013,31(6):1-3.

[5] 于晨曦,熊康宁,陈浒.喀斯特峡谷区干灾害成因初探与对策——以花江顶坛小流域为例[J].贵州师范大学学报(自然科学版)，2013,31(1):1-6.

[6] 吴士章,戚燕强,陈明华,等.黔中岩溶山区水稻田间需水量供需平衡研究[J].贵州师范大学学报(自然科学版)，2008,26(3):17-19.

[7] 李永梅,张学俭,张利根.基于BP神经网络的宁夏水资源需求量预测[J].水资源与水工程学报，2014,25(6):98-101.

[8] 刘丹丹,冯利华,王宁.基于反向传播神经网络的区域水资源需求量预测——以金华市为例[J].浙江大学学报(农业与生命科学版)，2011,37(2):231-236.

[9] 符传君,马超,许栋.基于灰色理论和神经网络的海口市水资源需求预测[J].水资源与水工程学报，2010,21(5):96-101.

[10]黄卫平.广西水资源供需灰色系统预测模型研究[J].广西水利水电，2005(2):5-9.

[11]乔松珊,孙成金,张建军.我国水资源量的灰色—加权Markov动态预测分析[J].河南科学，2014,32(11):2332-2336.

[12]钟晨煜,胡慧婷.基于灰色预测及多目标规划模型的水资源预测及优化配置[J].四川理工学院学报(自然科学版)，2013,26(5):90-95.

[13]秦剑.北京市水资源可持续发展动态平衡管理研究[J].管理评论，2014，26(5):30-38.

[14]邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1990:36-54.

[15]谢胜蓝,柯忠义,丁晓彤.仿柯布-道格拉斯生产函数的中国地区缺水量预测[J].节水灌溉，2014(3):85-88.

文章编号：1004—5570(2016)01-0022-06

收稿日期：2015-10-08

基金项目：国家自然科学基金资助项目(40806018)；国家水利公益性基金资助项目(201301055)

作者简介：刘帅(1990-)，男，山西运城人，硕士研究生，研究方向：水利水电技术经济及管理，E-mail:liushuaihhu1990@126.com. *通讯作者：袁汝华(1962-)，男，江苏兴化人，教授，研究方向：技术经济及管理,E-mail:yrh@hhu.edu.cn.

中图分类号：X196

文献标识码：A

Based on the Leslie matrix gray model for balance of supply and demand of water resources

LIU Shuai，YUAN Ruhua*

(School of Business, Hohai University, Nanjing, Jiangsu 211100, China)

Abstract:To explore the regional water resources supply and demand balance is the important premise of ecological environment protection. This paper selected 12 indicators in the supply and demand balance of water resources, then uses Leslie matrix model of quantitative indicators to measure and grey prediction model for gray prediction uncertainty index factors. Through the study of the empirical analysis of balance of supply and demand of water resources of Nanjing Yuhuatai district, and the results show that the prediction effect is better than traditional Leslie matrix and gray prediction effect, high fitting precision, accuracy effectively controlled within 5%.The model broaden the grey prediction model is applied in the balance of supply and demand of water resources, and also scientific prediction of water resources has a certain significance.

Key words:water resources; balance of supply and demand; grey system; Leslie matrix