结合“标准”要求浅析函数教学的三个关注点
何勇


摘 要:由于函数的概念高度抽象,导致学生在函数各类题型的解答中遇到许多问题,如学生对“运动变化过程中的规律”的理解不够透彻;难以从实际问题中建立函数模型;对从数据关系(列表)、图象特征(图象)和数量关系(解析式)三维角度研究函数性质的方法不够熟悉.本文参照“标准”要求,闡述了对初中函数教学的三点认识.
关键词:初中;函数教学
1 初中数学的课程目标和函数研究的内容与作用
1.1 初中数学的课程目标
《义务教育数学课程标准(2022年版)》(以下简称“标准”)指出:要培养的学生核心素养,主要包括以下三个方面:(1) 会用数学的眼光观察现实世界.在初中阶段,数学眼光主要表现为:抽象能力、几何直观、空间观念、创新意识;(2) 会用数学的思维思考现实世界.在初中阶段,数学思维主要表现为:运算能力、推理能力;(3) 会用数学的语言表达现实世界.在初中阶段,数学语言主要表现为:数据观念、模型观念、应用意识.
1.2 初中函数研究的内容和作用
函数是“数与代数”领域的主题之一.“函数”主要研究变量之间的关系,探索事物变化的规律.借助函数可以认识方程和不等式.数与代数领域的学习,有助于学生形成抽象能力、推理能力和模型观念,发展几何直观和运算能力.[1]
函数是高中数学的主线,关注函数的教学,有利于学生顺利完成初高中的学习衔接.
2 结合“标准”要求浅析函数教学的三个关注点
函数的概念高度抽象,是初中教学的难点.学生对“运动变化过程中的规律”的理解不够透彻;难以从实际问题中分析出变量之间的依赖关系,建立函数模型;对从数据关系(列表)、图象特征(图象)和数量关系(解析式)三维角度研究函数性质的方法不够熟悉;对利用函数思想求范围和最值的方法不够熟悉.
笔者参照“标准”要求,结合几道中考试题,谈一谈对初中函数教学的三点认识.
2.1 函数的教学要从概念、图象和性质多个角度进行诠释
2.1.1 从“标准”中找源头
【示例1】(“标准”实例72反比例函数的引入)尝试由xy=k(k≠0)所表示的关系过渡到反比例函数y=kx(k≠0).[1]
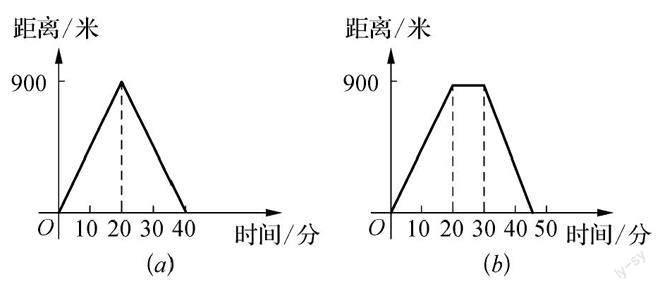
【示例2】 (“标准”实例68通过图象分析函数关系)如图,对于给定图象能够想象出图象所表示的函数关系.[1]
【示例3】 (“标准”实例80图形中心旋转的变与不变)在一个平面上,确定旋转中心和旋转角,通过多边形中心旋转的前后变化,分析运动过程中的变与不变.[1]
2.1.2 从“试题”中看对应
(2023无锡中考第17题)已知曲线C1,C2分别是函数y=-2/x(x<0),y=k/x(k>0,x>0)的图象,边长为6的正三角形ABC的顶点A在y轴正半轴上,顶点B、C在x轴上(B在C的左侧),现将△ABC绕原点O顺时针旋转,当点B在曲线C1上时,点A恰好在曲线C2上,则k的值为 .
感悟:本题结合折叠问题,考察抽象能力、几何直观、模型观念和运算能力,是对数学素养的综合考察.学生的答题难点有两个,一是从轴对称的角度把握折叠前后的不变量,引入合适的自变量x,建立S关于x的函数表达式;二是无理分式的化简对运算的要求较高.
“数与代数”和“图形与几何”交汇起来就是用代数的方法解决几何的问题.建立函数模型需要较强的几何直观能力,培养几何直观要重视两个方面,一是准确作图的能力,二是准确读图的能力.
运算是代数的灵魂,函数解析式和性质的研究都需要代数运算.教学中要重视幂、根式、整式、分式和应用乘法公式运算的渗透.
参考文献:
[1] 中华人民共和国教育部.义务教育数学课程标准(2022年版)[S].北京:人民教育出版社,2022.
[2] 王旭凤.如何提升初中函数教学的质量[J].华夏教师,2017(16):35.

