聚焦数形结合思想,巧解函数问题
俞航斌


摘 要:函数贯穿整个初高中阶段,不仅是数学学习的重要组成,也是数学学习的难点,更是考察的热点.在传统函数问题解答中,学生常常面临诸多问题,致使其频频失分.鉴于此,即可借助数形结合思想,旨在借助直观的图形,将复杂的函数问题简单化、具体化,拓展学生的解题思路,提升学生的解题效率.本文就以此视角切入,结合一定的例题,针对数学结合思想在函数问题中的具体应用进行了详细地探究,具备一定的参考价值.
关键词:初中数学;函数问题;数形结合;解题路径
函数问题贯穿初高中数学学习,也是数学学习的重难点.针对初中阶段来说,函数占据很大的比重,包括一次函数、正比例函数、反比例函数、二次函数等.同时,在最新的初中数学课程标准中,也对函数学习提出了新的目标:理解并掌握函数概念、解析式、图象性质特点,建立函数与方程不等式之间的函数,将函数知识灵活应用到实际生活中等.在这一背景下,初中函数已成为考察的重点.在调查中发现当前初中生函数问题解答能力比较低,致使学生在解答函数问题时常常面临诸多困难,甚至频频出现失分现象.鉴于此,唯有灵活融入数形结合思想,将抽象、复杂的数学问题进行转化,使其变得更加简单、具体,能够帮助学生拨开云雾,迅速找到解题的思路.
1 数形结合思想与函数问题解题
函数作为初中数学中的重要组成,学生在解答这一类型的问题时,不仅仅要掌握相关的数学基础知识,还应具备一定的解题技巧.在诸多函数解题技巧中,数形结合思想尤为常见.数形结合不仅仅是一种数学思想,也是一种非常重要的数学解题工具.关于数学这一学科来说,“数”和“形”是基本的研究对象,两者相辅相成、缺一不可,共同构成了数学学科的研究要素.同时,在最新的数学课程标准中,也对其提出了明确的要求,即:在组织和开展数学教学时,并关注学生的直观几何性,借助图形这一工具,对问题进行描述和分析,最终完成数学问题的解答.可以说,数形结合思想以其独特的优势,已经在函数问题、不等式问题、方程问题中得到了广泛的应用,不仅促进了抽象问题具体化、复杂问题简单化,也在很大程度上促进了学生思维的发展.
经课堂教学实践证明,将数形结合思想与函数问题融合到一起,可借助数形结合思想化复杂为简单、化抽象为具體,并发散学生的解题思维,真正提升学生的数学解题能力.除此之外,在数形结合思想的辅助下,还可将原本抽象的函数概念和性质等直观地展示出来,使得学生在形象感知中,对其形成深刻地理解和记忆,提升了学生的学习效果,为日后的函数解题奠定了坚实的基础;另外,数形结合解题训练也是一种数学思维训练模式,可促使学生在训练中,逐渐形成从多个角度分析问题的能力,不仅促进了思维的发展,也实现了数学知识的灵活运用[1].
2 数形结合思想在初中函数解题中的具体应用
2.1 数形结合,开拓解题思路
在日常函数解题教学中,存在一个常见的现象:相关的例题讲了很多,但是学生的函数解题能力始终停留在教师所讲解的题目中,只要条件稍微改变一下,学生便无从下手.导致这一现象的主要原因:教师在教学时,常常“就题论题”,忽视了“授之以鱼不如授之以渔”,致使学生在学习中并未真正领悟其中蕴含的数学思想,难以在学习中形成明确的解题思路.鉴于此,为了提升学生的函数解题能力,就必须要在日常解题教学中,适时融入数形结合思想,促使学生在图形的辅助下,形成一定的数学解题思维.
例1 若A(x1,y1)、B(x2,y2)、C(x3,y3)三点均在反比例函数y=2/x图象上,且A、B、C三点横坐标的关系是x1<x2<0<x3,则y1、y2、y3三者的大小关系是( ).
A. y3>y1>y2
B. y1>y2>y3
C. y2>y1>y3
D. y3>y2>y1
解析:这一题目考察的点是“反比例函数图象上点的坐标特征”,学生在解答这一问题时,唯有结合反比例函数y=2/x,并将其图象画出来(如图1所示),并对函数的图象进行判断,结果为:该函数图象分布在第一、第三象限之内.随即,学生即可结合函数图象所在的象限,判断出y值伴随着x的增加而逐渐减小.同时,再结合题目中所给的条件x1<x2<0<x3,即可精准判断出y1、y2、y3三者之间的关系为y3>y1>y2.
结合本题考查的知识点,如果按照常规的思路进行解答,常常需要耗费大量的时间和精神,不宜成为该题目的解答方式.在这一背景下,借助数形结合思想,在y=2/x函数图象的辅助下,即可精准确定y1、y2、y3三者的关系.
2.2 数形结合,培养解题思维
函数知识点集数和形于一体,一个函数可以用解析式进行表示,也可以用图形进行表示.这一点,不仅仅凸显了函数中蕴含的数形结合思想,也是学生解答函数问题的重要方法.在解决函数问题时,学生唯有融入数形结合思想,才能将原本抽象、复杂的函数问题进行转化,进而形成明确的解题思路.
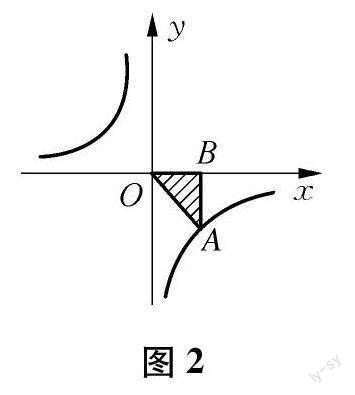
例2 如图2所示,点A在双曲线y=k/x上,且AB⊥x轴,垂足为B点,且△AOB的面积为2,则k的值为多少?
解析:这一函数题目主要围绕“反比例函数系数k的几何意义”进行考察,将函数知识与几何知识融为一体,难度系数有所增加.在具体解答这一问题时,结合反比例函数系数k存在的几何意义,以及函数所属第二、四象限的性质,即可将其确定出来.具体来说,结合题目中所给的条件,得知S△AOB=2,因此k=4.又因为y=k/x的图象分布在第二、第四象限之内,因此反比例函数系数k<0,即:k=-4.这一类型的题目在日常考试中尤为常见,做题的关键就在于正确理解k的几何意义,并结合图象分析进行解答[3].
例3 如图3所示,直线l1的解析式为:y=x+1,直线l2的解析式为:y=mx+n,两条直线相交于点P(a,2),那么,关于x的不等式x+1≥mx+n的解集是多少?
解析:这一题目将一次函数与不等式知识完美地融合到一起,充分体现了数学知识的特点.在解答这一问题时,如果按照传统的解题思路进行,学生需要结合两条直线的解析式,求出a的值,但是无法确定出m、n的值,只能得出两者的关系.面对这一现状,在引导学生解答该题目时,就可借助数形结合思想,将l1纵坐标大于l2的部分标出来,就可直接发现,包括P点在内的右侧部分,均是符合题目要求.同时,解题题目中所给的条件,因为P点的横坐标为a,且a=1.由此即可得出答案,该不等式的解集为x≥1.由此可见,在部分函数题目中,单纯地借助数学思维进行解题,常常会陷入到一定的思维困境中.此时,就可融入函数图象这一工具,通过图形分析,由图转数,最终即可轻松得出答案.
例4 证明方程(x-m)(x+n)=1必有两个实数根,且x1>m,x2<m.
解析:这一道证明题,如果按照常规的解题思路,先将其进行转化,使其成为一元二次方程,然后再通过判别式的大小,对方程实数根的个数进行判断,最后求解并与m进行比较.这种解题思路显然比较困难.此时,就可融入数形结合思想,根据方程转化成为函数,并画出函数图象.具体来说,假设y=(x-m)(x+n)-1,此时结合二次函数的性质,得出该函数的二次项系数大于0,因此该函数图象为开口向上的抛物线,又因为当x=m时,y=-1,因此,点(m,-1)在x轴的下方,据此就可将该函数的图象画出来(如图4所示).假设该抛物线与x轴存在两个交点,分别为A(x1,0)B(x2,0),且这两点位于(m,-1)的两侧,则存在x2<m<x1,且x1、x2则为方程的解.在本题目中,常规证明思路常常会受阻,唯有借助数形结合思想,将方程进行转化,构造二次函数,并据此画出图象,结合其性质进行证明.
2.3 数形结合,解决实际问题
新课程下,倡导培养学生解决实际问题的能力,真正实现知识的“学以致用”.函数问题在生活中也尤为常見.鉴于函数问题的特点,一旦遇到生活问题,将是难上加难,致使不少学生都出现失分的现象.针对这一现状,在引导学生进行解题时,就可融入数形结合思想,彻底攻克这一难题.
例5 花园中有一个圆形的喷水池,喷水池中间有个喷水柱正在喷水,水流从柱子的顶端朝着各个方向喷出,形成了条条抛物线(如图5所示),假设点A为喷水柱的顶端,点B为喷水抛物线的最高点,喷出的水流恰恰在C点落入到水池中.假设水流的高度y(米)和水平距离x(米)之间存在一个函数关系式,这一函数的解析式为y=-x2+2x+5/4.
求:(1) 喷水柱DA的高度.
(2) 水流喷出的最大的高度是多少?
(3) 要想保证该喷水池中喷泉的水不会喷到外面,则圆形水池的半径最小应控制在多少?
解析:这一问题就是函数在生活中的应用,以学生最为常见的喷泉作为题目素材,为学生设计了有关函数的问题.在第(1)问中,要求OA的高度,即可结合图象得知,当x=0时的纵坐标即为喷水柱OA的高度,通过函数解析式即可得出A点的坐标,即0,54,因此,OA的高度为1.25米;在第(2)问的解答中,水流喷出的最大的高度即为函数的顶点坐标,据此就可将函数进行转化,使其成为顶点式,得出y=-(x-1)2+9/4,最终得出水流的最高高度为2.25米;在第(3)问的解答中,就可将水池半径进行转化,使其成为方程-x2+2x+5/4=0的根,最终解方程得出C点的坐标为(2.5,0),因此水池的半径最小应控制在2.5米[4].由此可见,在这一题目中,解题的关键就是对生活问题进行转化,使其成为数学中常见的函数问题,再在基础上借助数形结合思想,利用图象分析即可轻松解答.
2.4 数形结合,规避常见的错误
在初中各种类型的考试中,函数问题尤为常见.部分学生虽然已经掌握了相关的知识,但在解题时忽略了数形结合思想的融入,致使解题中频频出现失误.面对这一现象,在引导学生规避解题错误时,就可借助数形结合思想这一工具,引导学生在代数和几何思维相结合的过程中,得出正确的答案.
例6 当-2≤x≤2时,求函数y=x2-2x-3的最大值和最小值?
解析:这是一道非常基础的函数最值问题,也是各大考试重点.部分学生在解答这一问题的时候,由于其忽略了数形结合思想的应用,导致其出现错误,即:分别将x=-2,x=2代入到函数解析式中,求出对应的值.当x=-2时,y=5;当x=2时,y=-3.据此得出该函数的最大值为5,最小值为-3.这一解题过程却是错误的,究其主要原因就是在代数思维的影响下,直接将自变量x的最大值和最小值代入到函数式中,误认为其对应的值就是函数最大值和最小值.
但是在解答问题时,如果融入了数形结合思想,就会出现不一样的答案.具体来说,先引导学生结合所学的内容,将函数y=x2-2x-3的图象画出来(如图6所示).
对图象进行观察得知,该函数是一个开口向上的抛物线,根据所学知识,很轻松得出其对称轴为x=-b/2a=1.因此,当x=1时,y最小=-4.之后,再将x=-2带入到函数解析式中,得出y=5;将当x=2带入到函数解析式中,得出y=-3,因为-3<5.因此,当x=1时,函数y=x2-2x-3存在最小值,y最小=-4;当x=-2时,函数y=x2-2x-3存在最大值,y最大=5.由此可见,在解答部分初中函数问题时,一旦忽视了数形结合思想的运用,按照常规的代数思维解题,就会出现各种各样的错误,而在数形结合的辅助下,则能有效规避这一现象,不断提升学生的数学解题正确率.
3 结语
综上所述,在数学学习中,数轴打开了数形结合思想的帷幕,随之而来的不等式、函数等知识,都必须要依托于一定的数形结合思想,才能形成深刻的理解,才能灵活解决相关的问题.尤其是在新课程改革背景下,数形结合思想作为一种重要的数学思想得到了前所未有的重视.鉴于此,作为一名初中数学教师,唯有立足于具体的内容,将数形结合思想融入到函数日常教学、解题训练中,才能促使学生在潜移默化中形成一定的数形结合思想,并在这种意识的支配下,将其灵活应用到日常解题中.
参考文献:
[1] 姚静娴.初中函数教学渗透数形结合思想的研究[D].扬州大学,2022.
[2] 方福强.浅析初中函数“数形结合”的解题策略[J].新课程(下),2019(4):88.
[3] 廖琼.试论数形结合思想在函数解题技巧中运用的价值[J].读写算,2019(10):192.
[4] 雷红,杨文.数形结合思想在初中数学解题中的应用——以初中函数问题为例[J].福建中学数学,2019(2):4648.

