“双减”背景下的初中数学单元作业设计
——以“平行四边形复习课作业”为例
广州市真光中学
苏国东
作业是课堂教学向课外的延伸与拓展,是提高教学质量,促进学生核心素养发展的有效途径.“双减”政策给学校教育带来了巨大改变,对教师的教学能力和作业设计能力提出了更高的要求.单元作业更成为了巩固知识、减负增效的重要手段.
1 单元作业设计案例
本案例是针对人教版八年级下册第十八章“平行四边形”的单元复习课,设计的一份作业题组.
基于《义务教育数学课程标准(2022版)》(以下简称“课标”)、人教版数学教材,以及“双减”对作业设计提出的减负增效的要求,对于本案例笔者采用了“2+2+1”分层作业设计,即一份作业中包含两道基础题、两道提升题和一道拓展题.
1.1 课标要求分析
平行四边形是“图形与几何”模块的重要内容,是平行线、三角形等知识的应用与深化,为后续进一步研究复杂的几何问题做好知识和能力储备.
(1)课标对本章节内容的要求如下:
①理解平行四边形、矩形、菱形、正方形的概念,以及它们之间的关系.(对应作业第3,5题)
②探索并证明平行四边形的性质定理及判定定理.(对应作业第1,3题)
③探索并证明矩形、菱形、正方形的性质定理及判定定理.(对应作业第2~5题)
④探索并掌握三角形的中位线定理,以及直角三角形的性质定理(即直角三角形斜边上的中线等于斜边的一半).(对应作业第3,5题)
(2)本单元作业中还综合考查了全等三角形、勾股定理、垂直平分线等知识,课标对其要求如下:
①能识别全等三角形中的对应边、对应角;掌握基本事实,即两角及其夹边分别对应相等的两个三角形全等;证明定理,即两角分别相等且其中一组等角的对边相等的两个三角形全等.(对应作业第4,5题)
②探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问题.(对应作业第2,3,5题)
③理解线段垂直平分线的概念,探索并证明线段垂直平分线的性质定理,即线段垂直平分线上的点到线段两端点的距离相等.(对应作业第2,5题)
1.2 学情分析
八年级学生在本章的教学中已经学习了平行四边形章节的新授课知识,较熟练地掌握了全等三角形、勾股定理、垂直平分线等知识,具备一定的应用基础,但缺少系统复习和整理以及知识的综合运用.
通过课堂的复习教学,学生经历了独立思考、小组合作、活动展示等环节,对本章节进行了结构化整理,巩固了平行四边形、矩形、菱形和正方形的性质和判定,以及添加边、角、对角线进行各种四边形相互转化的方法,能较规范地进行解答题的书写,初步了解了分类讨论、转化与化归等数学思想方法.但部分学生复习效果不佳,对菱形面积等公式记忆不清,对添条件问题、添加辅助线解题的方法较为生疏;受课堂容量的限制,对综合性问题无法过多展开和应用.
1.3 作业目标设计
基于上述课堂教学现状,笔者给出了相应的练习补充,设计由浅入深,又深入浅出,有效巩固和提升学生本节课的学习效果.
本单元作业设计的目标,是让学生能熟练运用四边形各种性质和判定进行基本的计算与证明,体会图形之间的转换过程.通过分析条件和结论的关系,构造辅助线,综合运用全等三角形、勾股定理等相关知识,比较不同的方法,探究开放性的拓展题,逐步形成研究几何问题的基本思想和方法,提高逻辑推理能力和数学核心素养.
1.4 作业内容
【基础题】

图1
(1)(人教版八年级下册第49页习题第3题)如图1,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,则△OCD的周长是______.
设计意图:选取教材配套题目,改为填空的形式呈现,考查学生对平行四边形性质的掌握情况.
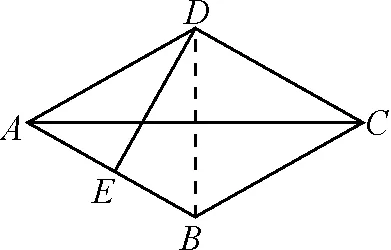
图2
(2)如图2,在菱形ABCD中,点E是AB的中点,DE⊥AB,AB=2,则AC=______,菱形ABCD的面积为______.
设计意图:考查学生对菱形性质及面积公式的熟练运用,融入垂直平分线、等边三角形、勾股定理等知识,体现了作业对课堂教学内容的有效巩固与补充.
【提升题】
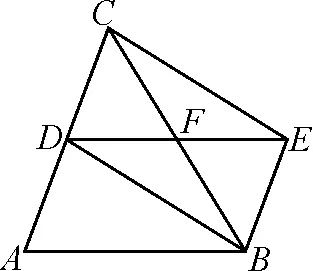
图3
(3)如图3,四边形ABED是平行四边形,D是AC的中点.
①给△ABC添加一个条件,使四边形BECD成为矩形,你添加的条件是______;
②给△ABC添加条件,使四边形BECD成为正方形,你添加的条件是______.
设计意图:题图源于教材第48页探究三角形中位线性质的图形,以填空题的形式设计成开放性问题,沟通了两个特殊四边形的联系,发散学生思维,集中考查了学生对各种四边形的判定及其相互转换的掌握情况.

图4
(4)(人教版八年级下册第69页复习题第14题改编)如图4,四边形ABCD是正方形,点E是边BC上的一点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.求证AE=EF.
设计意图:省去教材原题条件“点E是边BC的中点”以及提示语,改编出本题,考查了正方形的性质、全等三角形以及构造辅助线等相关知识.本题实际上是一个动态问题,让学生感受教材原题的结论在一般情况下仍然成立;同时,结论可进一步推广,与近年考题相互衔接,发挥出教材例题、习题的功能,凸显考题回归课标和教材的本意.
【拓展题】
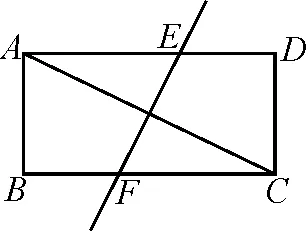
图5
(5)如图5,在矩形ABCD中,对角线AC的垂直平分线分别交AD,BC于点E,F,若BF=6,AE=10.
①求AC,EF的长;
②在AC上是否存在点P,使得∠EPF=90°?如果存在,请求出AP的长;如果不存在,请说明理由.
设计意图:第①问考查了矩形的性质、菱形的判定、垂直平分线的性质、构造辅助线、全等三角形、勾股定理等知识.该问设计成解答题,要求学生不仅要知其然,还要知其所以然;同时进一步规范学生的书写格式,对课堂的复习效果作出检验和拓展.
第②问充分挖掘图形的内涵,巧妙设计成探究性问题,实际考查了“直角三角形斜边上的中线等于斜边的一半”的应用.学生需要找到思考的切入口,联想已学的知识和方法,构造辅助线,分类讨论,运用创新性思维解决问题,促进其数学核心素养的发展.
2 单元作业设计建议
2.1 立足课标,深挖教材
“课标”作为教材编写、教学、命题和评估的重要依据,具有不可替代的导向功能,其以了解、理解、掌握等不同目标层次,指出了作业设计的覆盖面和侧重点;而教材严格依照课标编写,准确反映了课标对数学课程内容的要求,教材的例题和习题更是历年数学试题命制的重要来源,不可脱离.作业设计应当遵循课标导向,厘清教材立意,挖掘题目内涵,提升品质和价值.
2.2 关注课堂,变式拓展
基于课堂教学实际情况,配套作业应予以有益补充,做到精确校正课堂教学,引导学生自主探究,进一步巩固和提升学生课堂学习的效果.单元复习课的作业设计,可以对教材单元例习题、课堂教学问题进行变式改编,巩固补充(如本作业中第1,2,4题),注重对阶段教学内容的总结和归纳;又可以根据单元教学重难点,设计探究性、拓展性问题(如本作业第3,5题),关注对综合性问题的进一步拓展探究.同时,要重视作业的点评与交流,使作业发挥持久的价值.
2.3 落实双减,提质增效
作业设计方式的变革,是切实提高教学质量,培养学生数学核心素养的有效途径.基于“双减”背景,作业设计要体现减负提质增效的内涵;立足课标与教材,重视不同层次学生的学习需求和完成作业的能力,做到精选问题、分层兼顾、把控容量,提升数学作业设计的多样化、个性化与开放性;减轻学生过重的作业负担,增强作业的综合育人功能,培养学生克服困难的信心,推进“双减”政策的精准落地.

