重视概念生长过程 搭建单元知识框架
——“认识分式”(第一课时)教学设计与思考
广东省深圳市龙华区博雅实验学校
管志刚
“数学概念是产生数学知识的基础,是提炼数学思想方法的平台,是积累数学活动经验的载体,是数学学习的内核.”[1]数学概念的教学过程,为培养学生用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界提供了得天独厚的平台.所以,数学概念的教学,要重视概念的生长过程,凸显概念的必要性、必然性和合理性.本文是笔者执教北师大版“认识分式”第一课时的教学设计,以及对概念教学、单元统领教学的几点思考,与大家探讨.
1 教学内容分析
分式和整式都属于代数式,它们之间有着密不可分的联系和本质上的区别.二者定义的方式是否一样,学习的思路是否一致,性质和运算方法是否相同,等等,这些都等待着学生去学习和探索.生长数学教学主张认为,分式概念的主要属性有:(1)分式表示除法运算(也可以表示成带有分数线的形式);(2)被除数和除数都是整式(分子和分母都是整式);(3)除数中含有字母(分母中有字母).因此,本节课教学的关键就是要通过问题情境,让学生抽象出分式的数学属性,并在此过程中,让学生感受概念的生长过程、感悟建立此概念的必要性和必然性.
2 教学活动设计
环节一:导入新课
问题1已知长方形的面积为7 cm2,宽为3 cm,则长方形的长为cm;若宽改为bcm,则长方形的长为cm.
问题2已知长方形的面积为acm2,宽为bcm,则长方形的长为cm;若宽增加2 cm,则长方形的长为cm.
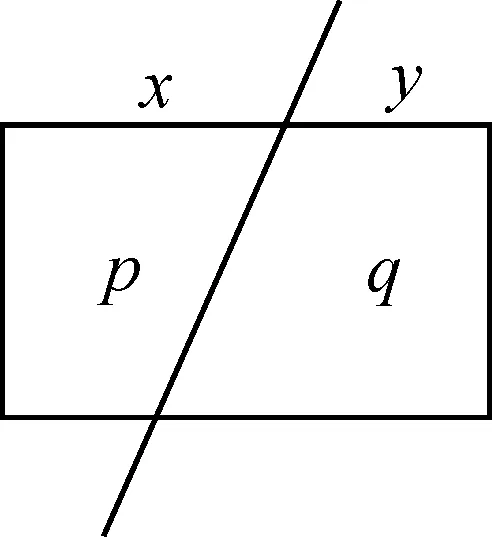
图1
问题3如图1,矩形被一直线分成面积为pcm2和qcm2的两部分,对应的边长分别为xcm和ycm,则矩形的宽为cm.
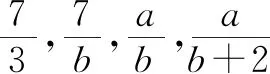
环节二:概念生成

问题5你们能否再写一些满足这些特点的代数式呢?

问题7这样的例子有无数多个,我们该怎么刻画这些特点?
问题8像这样的式子我们称为分式,那你现在能给分式下个定义吗?

环节三:概念辨析
问题9下列各式中,哪些是分式?哪些是整式?
设计意图:问题9是第五个环节——“再辨析”.“再辨析”是根据概念的内涵与外延,帮助学生进一步认清概念的本质,以便学生应用概念解决问题. 在这个环节中,教师可设置一些稍有难度、迷惑性较强的代数式让学生辨别.
环节四:拓展探究

问题11在问题10中可以发现,分式的值可以是正数,也可以是负数.分式的值可以为0吗?

设计意图:问题10旨在让学生了解分式,它的值是随着字母的取值变化而变化;问题11旨在让学生自主发现分式值为0的条件;问题12旨在引导学生自主探索分式有意义的条件.之后,教师还需要引导学生发现之前仅从形式上定义分式是不完善的,必须加上分母不为0这个条件.因此,我们用“样子”+“条件”的方式定义分式,二者缺一不可.
环节五:针对训练



环节六:结构统领
问题13小明和小红计划周末去广州长隆欢乐世界游玩.已知深圳到广州的距离约为140 km, 小明选择自驾前往,汽车的平均速度为xkm/h,小红选择高铁出行,高铁的平均速度是汽车的3倍多10 km/h.小明和小红同时出发,小红比小明提前一小时到达广州,求汽车和高铁的速度分别是多少?
设计意图:引导学生在解决实际问题中抽象出新的模型——分式方程.继续求方程的解,则有必要先学习分式的性质和四则运算,这样就能很好地统领整个章节的知识,搭建知识生长的框架.同时,教师还可以引导学生类比整式的学习,发现分式的学习套路和整式的学习套路一脉相承,加深学生对于代数式学习的理解.
3 活动设计的思考
3.1 概念自然生成是概念学习的根本所在
本节课通过“给例子—找属性—再举例—下定义—再辨析”五个环节,让学生经历了概念的生成过程,感受了建立分式概念的必要性和必然性.具体来说,环节一的问题情境阐明了分式“从哪里来”,即分式是描述现实情境的一种重要模型.环节二让学生去找这些代数式的共同特点,归纳其共同的数学属性.待学生有一定的理解之后,环节三再次聚焦相同属性,让学生举出一些具有这些属性的例子.那些在“找属性”环节中没有任何发现的同学往往举不出新的例子,或者容易写出错误的例子,这些都是对属性理解不到位和不深刻的体现.厘清分式属性之后,分式的概念就呼之欲出了,用数学语言将发现的共同属性表达出来即可.教师可以先让学生大致地说一说,再细致地优化为教材中的语言.分式相对于整式而言有一个特殊的地方,就是分式在字母赋值的时候可能会导致分式无意义,因此在分式的概念中必须补充这一点,这是概念“精致”的过程.因此,笔者认为概念教学一般要经过大致地描述、细致地优化、精致地补充三个过程.
3.2 巧设问题情境是知识构建的重要途径
教学是提出问题、解决问题的持续不断的过程,提问是课堂教学的主要形式,也是师生交流的重要途径.教师提问,学生作答,这看似平常的教学环节却关系到课堂教学是否有效、实效、高效.数学课堂上,高质量的提问是学生参与课堂、理解数学概念、参悟数学本质的重要途径.


3.3 搭建知识框架是点睛之笔
本节课是章节的起始课,在一定程度上起着承前启后、开山引路的作用.教师在教学时要对整章内容做一个提纲挈领式的“预览”,搭建知识框架,使学生在开展后续的学习之前对整章内容有一个全局认识,起到统领全章的作用,避免“只见树木,不见森林”[2].所以本节课在利用分式解决实际问题的环节中,学生抽象出一个新模型——分式方程.而学生在求解分式方程的过程中,会意识到要先学习分式的性质和运算才能解分式方程.通过这样的设计,学生就能了解本章所有知识的建构过程,整体把握知识间的逻辑结构.同时,教师再加以引导,将 “现实情境—定义—性质—运算—应用”的学习模式和有理数、整式的学习模式统一起来.这样的引导对学生数学学习能力的培养、学习兴趣的提升的和探究精神的养成等都有一定的价值.

