基于默会知识的初中数学概念教学路径探寻

江苏省江阴初级中学

刘一萍

默会知识就是一种大家都在用，只可意会不可言传的知识，是相对于明确知识而言的.默会知识的特点包括：一是情境性，是基于情境的一种直观感受；二是实践性，在实践中应用与意会；三是主体性，主体只有参与实践才会领会.学生每学习一个概念，都会启动相应的默会知识，在学习任务下，自觉搜索、联想默会知识，从而让新知在头脑中复活.

1 概念引入，启动默会知识

默会知识是基于情境的一种直觉感受，具有情境性.因此，创设一定的情境，可以启动学生的默会知识，让学生的思维进入积极的状态.例如引入“轴对称”时，学生对于轴对称的默会知识：自然界看到的花蝴蝶，校园里的教学楼，人的脸，大众的车标，奥运会的五环旗，等等.因此，笔者根据学生的生活实际体验设计这样的情境：出示一些轴对称图形和一些非对称图形，让学生思考哪些图形看起来比较有美感，然后，让学生探索轴对称图形具有美感的原因，以引发学生对于轴对称图形特征的默会经验.

1.1 以解决实际问题引入

(1)基于生活实际，提供现实原型

通过生活实际，引导提炼概念的本质特征.比如，教学“坐标系”的概念时，笔者引入世界地图，每一个地点的位置都有经度与纬度两个数值；看电影时，买的电影票写着几排几号，用一对有序实数表示平面内的点的位置.在生活情境中，学生把默会知识与数学概念“坐标系”对比，经历了概念的发现过程.

(2)基于实验情境，学生直观演示

通过设计数学实验活动，学生动手操作，在观察、比较、体验中，体会概念的特征.比如，关于“正方形”概念的教学，笔者让学生用一张矩形纸片折出一个面积最大的正方形，学生将纸片宽的一边与它的长边的一部分重合进行折叠，然后把剩余的部分裁掉，得到一个正方形，在动手操作中，理解正方形邻边相等的本质特征.

(3)还原概念的发展演变过程

数学概念的产生经历了一个长期发展与演变的过程.比如，无理数的概念，在无理数发现以前，人们认为现实生活的一切量都可以用有理数来度量.毕达哥拉斯的学生希帕索斯在研究直角三角形时发现，直角边为1的等腰直角三角形的斜边长不是一个有理数，即斜边长无法用一个整数或两个整数的比来表示，并给出了证明.于是，无理数被发现了，它是无限不循环小数.

1.2 在原有的知识基础上引入

数学知识是环环相扣的演绎体系，数学概念之间都有逻辑联系.对于有逻辑关联的概念，可以通过逻辑推理的形式同化概念，引入的方式多种多样，取决于新旧概念之间的关系.

(1)旧概念包含了新概念

在旧概念的基础上添加新的限制条件，形成新的概念.如教学“菱形”概念时，笔者给学生出示了许多一般的平行四边形及菱形，让学生发现其中形状特殊的平行四边形，学生很快看出菱形与一般的平行四边形有所不同：菱形虽然也是平行四边形，但它的四条边相等.于是得到了有一组邻边相等的平行四边形是菱形的概念.

(2)新概念包含了旧概念

如教学“实数”概念时，笔者给学生出示了一些有理数，又出示了一些无理数，然后把这些数合在一起，即所有的有理数与无理数叫做什么数呢？促使学生必须提出一个新概念来概括这些数，于是产生了实数的概念：有理数与无理数统称实数.

(3)新、旧概念之间具有相似性

如，教学中，笔者类比分数的性质与运算法则，引入分式的性质与运算法则；类比一元一次方程的概念，引出一元一次不等式的概念；类比一元一次不等式的概念，引出一元二次不等式的概念.

(4)基于先行学习经验

如，反比例函数学习中，笔者引导学生回顾研究一次函数的一般过程，一次函数的概念—图象—性质—一次函数的应用，从而确定学习反比例函数的一般历程，反比例函数的概念—图象—性质—反比例函数的应用.

2 概念抽象，应用默会经验

教师引导学生经历概念形成的一般过程为：观察分析具体实例，然后概括同一类事物的本质属性，最后用自己的语言刻画本质属性，形成概念.

比如，教学“正方形”的概念时，要求学生用矩形纸片折出面积最大的正方形后，用自己的语言描述正方形的概念.此时，学生需要通过前面描述概念的经验，对照正方形的本质属性进行表述.当然学生的语言有时不够精炼准确，此时，教师要引导学生加以修正.学生在表达概念过程中，学生的默会知识与正方形概念的本质属性建立了联系，从而能明确提取概念的本质，最后，用简练的文字、公式、图表、图象予以表达，实现了默会知识的外显化，在概念生成的过程、参与新概念与默会知识的互联中，掌握了使用默会知识的经验.

学生的表达需要一定的反馈评价，基于课堂实际，无法让每一个学生在全班表达.此时，教师可利用小组合作的形式，让每个同学都有表达的空间与时间，用自己的语言表达概念.小组宽松的氛围，不仅能激活学生的默会思维因素，还能发挥内隐学习机制的作用.

3 概念辨析，更新默会知识

刚学完新概念，学生的认知结构还不够稳固，还没有形成清晰的默会知识，这就需要教师引导学生运用正反实例进行比较、辨析，摆脱非本质属性的干扰，用明确的知识语言，以及符号表达新形成的默会知识，概括其本质特征，进而内化为新的默会知识.

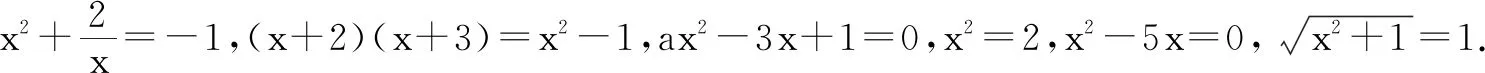
又如，教学“概率”的概念时，笔者让学生做抛掷图钉的实验，然后统计抛掷次数与针尖不着地的频数，并计算针尖不着地的频率，结果如下表所示.

抛掷次数频数频率100640.642001180.593001890.634002520.636003600.608004880.6110006100.61

针尖不着地的概率是多少？有学生说是0.60，因为表格有这样的频率，有学生说是所有频率的平均数.此时，笔者引导学生回顾概率的定义，事件发生的概率是指随机事件发生频率的稳定值，实验次数越多，估计越准确，所以针尖不着地的概率应选0.61.

4 概念应用，培养默会能力

在运用概念解决问题时，如何提升学生的默会能力呢？

一是让学生独立思考，在实际问题情境中，自觉搜索相应的默会知识，在任务的驱动下，自觉对照与比较概念特征，找出转换情境的关键点，进行一系列的思维加工.比如，在应用概念的过程中，笔者让学生独立思考，获得自己的想法与体验，学生经过积极努力尝试，调动了默会知识的主体意识.学生自主思考后，自然会引起讨论，此时，笔者引入小组合作，尝试引导学生交流讨论，在组内暴露自己的疑惑与错误，实现思维共享.最后，笔者适时指导，培养学生的默会能力，给学生表达的机会.

二是让学生说思维过程，让学生明确知识的逻辑形式，借助符号与语言表达默会知识，加工默会知识.在此过程中，学生经历了失败到成功，以及从错误到正确的调整，提炼了一般方法经验，提升了默会能力.

5 概念系统化，发展默会潜能

反思学习概念的过程及研究策略，有利于完善概念的认知机制.数学概念虽然多，但是数学概念之间有很强的逻辑关系.在总结概念阶段，教师要引导学生把握概念的内在联系，整合所学概念，把所学新概念纳入已有概念框架，形成新的默会体系，建立科学的概念网络体系，进而提升默会潜能.

总之，概念教学是一个不断螺旋上升的过程.在教学中，教师要以任务驱动的形式，提取相应的默会知识，通过明确的知识语言与符号表征，使默会知识显性化，使内隐的学习有规则可循，进而发挥默会认知潜能.