数学概念的教科书呈现方式探究
安徽省阜阳市第一初级中学
张倩影
数学概念的形成离不开实际生活,初中阶段的数学知识大多反映了实际生活中的数量关系.因此,在初中数学教学中引入数学概念时要将其与学生生活实际密切联系,使学生能够更好地体会数学概念的应用场景,以便于理解概念的实质并加以灵活运用.下文将以“一元一次方程”为例,探究数学概念的教科书呈现方式.
1 数学概念的教科书呈现方式设计理念
数学概念在教科书中呈现方式的设计要充分体现数学概念的抽象、归纳过程,从而在学生理解性掌握数学概念的基础上,不断获得数学思维的发展,最终促进基本思想、基本活动经验的有效形成.故此,应增加对数学概念在教科书中呈现方式的关注力度,并实施切实可行的方案,将数学概念的抽象过程充分利用起来,在掌握数学知识的基础上促进学生数学素养的提升.
2 数学概念的教科书呈现方式典型案例设计
为进一步促进学生数学素养的培养以及提升,本研究将围绕初中数学一元一次方程概念的设计,以教科书上呈现出的体现学生归纳与抽象素养的培养为导向,帮助学生在学习数学知识以及数学概念掌握的过程中积累抽象、归纳和总结等经验,不断促进学生抽象、归纳和总结素养的提升.
2.1 一元一次方程的文本内容在教科书中的呈现
(1)问题表述
小明用72元买了10份汉堡包和爆米花,假设每份爆米花为6元,每份汉堡包为8元,请计算小明共买了几份汉堡包.
(2)模型构建
第一步,围绕问题展开分析,探索其中的关系,应用自然语言具体描写.上述问题中具有多个变量,并且各个变量之间具有一定的关联性,其中相等关系分别为
总钱数=购买汉堡包钱数+购买爆米花钱数;
总份数=汉堡包份数+爆米花份数;
购买汉堡包钱数=汉堡包单价×汉堡包数量;
购买爆米花钱数=爆米花单价×爆米花数量.
第二步,用符号表达上述关系.设▲表示汉堡包的份数,★表示爆米花的份数,上述表达式即可表示为
▲+★=10(份),8×▲+6×★=72(元).
第三步,应用数学符号表达上述关系.设购买汉堡包的份数为x,则上面的关系表达式为
x+★=10(份),8x+6×★=72(元).
故购买爆米花的份数为10-x,上述关系式可进一步简化为8x+6×(10-x)=72.
此类含有未知数的等式,即为方程.
(3)练一练

例2食堂内有煤若干,原来每天烧煤3 t,用去15 t后进行设备的改进,耗煤量为原来的一半,结果多烧了10天,计算原来存煤量.
(4)想一想
8x+6×(10-x)=72是只含有一个未知数x的方程,且未知数的次数为1,此类方程为一元一次方程,那么3×(5a+4b)+2×(5a+7b)=1 500这个方程应该叫什么方程呢?
(5)解释应用
例3结合科学营养搭配理念进行猪饲料的配置,是开展科学养猪的一项重要环节.在某养殖场内,应用玉米、菜籽粞进行一头猪(60 kg)日粮的制备,从而保证能够与其营养需要标准(如表1)相符.

表1
结合预设的养殖标准,每一头体重超过60 kg的肥猪CP需要选为13%,DE需要选为3.2 Mcal/kg.为明确玉米配合比例为多少方能符合要求,应如何列出方程?
第一步,用自然语言描述问题所具备的等量关系如下:
CP总含量=玉米内CP含量+菜籽粞内CP含量;
1=玉米配合比例数+菜籽粞配合比例数;
玉米内CP含量=玉米的CP含量×玉米配合比例数;
菜籽粞内CP含量=菜籽粞的CP含量×菜籽粞配合比例数.
第二步,应用半符号语言表达上述关系.
用▲表示玉米配合比例数,用★表示菜籽粞配合比例数,则上述关系可表示为
9×▲+38×★=13,▲+★=1.
第三步,用数学符号语言表达等量关系.
假设玉米配合比例数为x,则上述关系可表示为:9x+38×★=13,x+★=1.
整理分析后,可得出9x+38×(1-x)=13.
经计算可知,当x≈0.862 1时上述方程成立.
(6)随堂练习
练习1 请找出以下方程中的一元一次方程:
①5x+3=18;
②0.6x+2.4=1.2x;
③y-2x=8;
④x2+4x=16;
⑤3t-21=6-t.
练习2 足球表面有32块黑色五边形与白色六边形,黑色与白色皮块的块数比为3∶5.
①假设白色皮块有x块,可得出怎样的方程?
②假设黑色皮块有y块,可得出怎样的方程?
练习3 列一元一次方程式:
①假设一桶方便面的单价为x元,一桶方便面比一瓶矿泉水贵3元,乐乐准备买2桶方便面与3瓶矿泉水,共需要支付多少钱?如若20元刚好足够购买2桶方便面与3瓶矿泉水,可得出怎样的方程?
②一个长方形的长比宽多3 cm,假设周长为26 cm,请计算长方形的宽为多少.
(7)习题

习题2 结合下列语句设置适当的未知数,并列出一元一次方程:
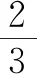
②某数的相反数比它的2倍多5.
习题3 根据下列各题建立方程:
①某家商店将一种商品按照成本价提升40%后标价,元旦期间欲采取八折销售,以答谢新老顾客对商店的光顾,售价为224元,那么该商品的成本价为多少元?
②学校准备2 000元资金用于购买“希望杯”数学竞赛奖品,一等奖每人200元奖品,二等奖每人50元奖品,计算获得一等奖、二等奖的人数.
2.2 设计说明
方程是反映现实生活中等量关系的一种数学模型,用数学符号表达现实生活中特定的等量关系,建模以及化归是方程思想的核心与关键.这是教科书设计理念的依据.在教学中,教师应于初期阶段引导学生联系现实问题,运用数学语言表示日常生活中的自然语言,最后得出方程并求解,从而利用方程解决实际问题.故此,初中数学教师应指导学生从实际生活问题出发,进行大量有关生活问题的分析以及概括.具体流程如下:先找等量关系,再用半符号化语言表达等量关系,最后用符号化语言表达等量关系即列出方程.具体而言就是引导学生于题目中探寻等量关系,并应用文字语言表述,在合理假设未知数后以半符号语言表达等量关系,并应用图示的方式直观表示等量关系,最后列出方程.
这样的概念整体呈现流程可有效体现解决问题的思维过程,对学生活动经验的积累以及学生数学素养的提升均具有积极意义.
3 结束语
综上所述,在初中数学课程设计环节中,应加强对数学概念抽象归纳过程的重视程度,从而进一步提升数学课程基本理念,更好地实现对学生数学素养的培养.另外也要注重初中数学教科书中概念呈现方式的变化,系统、全面地对初中数学核心概念进行抽象、归纳和整理,不断深化学生对概念的理解程度,为提升初中数学教学效率以及质量提供保障.

