高中数学教学中几何画板的运用
吴启明
摘 要:在高中数学教学中,几何画板作为一种强大的教学工具,为学生提供直观、动态的学习环境.特别是在函数教学中,可以帮助学生更好地理解函数的概念、性质和应用,通过绘制函数图象、探索函数的变化规律以及解决实际问题,使学生深入掌握函数的本质.本文以高中数学教学为核心,先行阐明几何画板运用意义,继而以函数教学为例,指明几何画板的具体运用,最后提出几点运用建议,以供参考.
关键词:高中数学;几何画板;教学运用
几何画板在高中数学函数教学中的应用能够激发学生的学习兴趣,提高学生的空间想象力和问题解决能力,学生也可以通过自主探索和实践,培养自己的数学素养和创新能力.在这一背景下,教师应充分利用几何画板的优势,设计丰富多样的教学活动,激发学生的学习兴趣和积极性,提高教学效果.
1 高中数学教学中几何画板的运用意义
1.1 直观展示函数图象
几何画板可以帮助学生更加直观地理解和掌握各种函数的图象,通过使用几何画板绘制函数的图象,学生可以清晰地看到函数的形状、对称轴、顶点等重要特征,从而更好地理解函数的性质和变化规律,这对于学生理解函数的定义域、值域、单调性、奇偶性、周期性等概念帮助较大.
1.2 动态演示函数变化
除了绘制静态的函数图象,几何画板还可以通过动态演示函数的变化过程,帮助学生更深入地理解函数的性质,如通过拖动函数图象上的点观察函数值的变化,或者通过改变函数的参数观察函数图象的变化.这种动态演示的方式可以让学生更加直观地感受到函数的单调性、奇偶性、周期性等性质,从而更好地掌握函数的概念[1].
1.3 帮助理解函数概念
函数是高中数学中重要的概念之一,但是函数的概念比较抽象,学生理解起来比较困难.通过使用几何画板,学生可以更加直观地理解函数的概念和本质,如通过绘制函数图象理解函数的定义域和值域,通过观察函数图象的变化理解函数的单调性和奇偶性等概念.这种直观的方式可以让学生更加深入地理解函数的概念,从而为后续的学习打下坚实的基础.
1.4 提高学生的空间想象力
几何画板可以帮助学生提高空间想象力,培养学生的几何直观能力.通过绘制各种几何图形和函数图象,学生可以更好地理解几何图形的性质和变换规律,从而提高自己的空间想象力和几何直观能力,这种能力对于学生学习数学和其他学科都非常重要.
1.5 增强学生的学习兴趣
几何画板可以通过绘制各种有趣的函数图象和几何图形,激发学生的学习兴趣和好奇心.学生可以通过自己动手绘制函数图象和几何图形,体验数学的乐趣和美妙,从而增强学习数学的信心和兴趣,这种积极的学习态度对于学生的学习和成长非常重要.
2 高中数学教学中几何画板的具体运用
2.1 函数图象的绘制
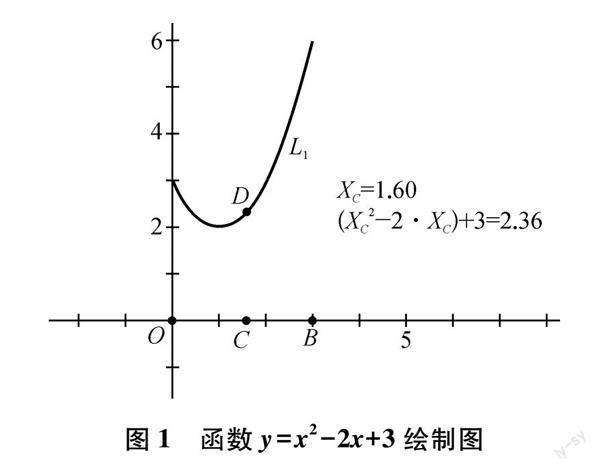
在高中函数教学中,几何画板可以用来绘制函数图象,下面以人教B版教材中的函数y=x2-2x+3为例,展示如何利用几何画板绘制函数图象.
(1) 打开几何画板,在x轴上绘制出点B(3,0),构造线段OB.
(2) 在O与B之中任意选择一点为C,度量出点C的横坐标xC.
(3) 选中点C的横坐标,利用“计算”菜单命令,计算出xC2-2xC+3的值.
(4) 绘制出点D(xC,xC2-2xC+3),同时选中点C和点D,构造出点D的轨迹,即为函数图象的一部分.按照同样的方法,可以构造出函数图象的另一部分,从而得到完整的函数图象.如下图所示:
在绘制过程中应注意以下几方面:(1) 函数的表达式.在绘制函数图象之前,需要确保输入正确的函数表达式.如果函数表达式有误,将导致绘制出的图象不准确.(2) 坐标轴的范围.在绘制函数图象时,需要设置合适的坐标轴范围,以确保图象能够完整地显示出来.如果坐标轴范围设置不合适,将会导致图象被截断或缩放,影响对函数性质的观察和分析.(3) 图象的标注.在绘制函数图象时,需要对图象进行标注,如坐标轴标签、函数表达式等.标注应清晰明了,以便学生更好地理解函数的性质.(4) 图象的颜色和样式,在绘制函数图象时,可以选择不同的颜色和样式表示不同的函数.颜色和样式的选择应根据函数的性质和特点确定,以帮助学生更好地理解函数的性质.(5) 动态演示,几何画板可以通过动态演示函数的变化过程,帮助学生更好地理解函数的概念和性质.在使用动态演示功能時,需要注意控制演示的速度和范围,以避免学生无法跟上演示的节奏的情况[2].
2.2 函数性质的探究
在高中函数教学中,几何画板可以用来探究函数的性质,下面以人教B版教材中的函数y=x2-2x+3为例,展示如何利用几何画板探究函数性质.
(1) 绘制函数图象:使用几何画板绘制出函数y=x2-2x+3的图象,可以通过选择【图表】菜单中的【绘制新函数】命令,输入函数的表达式绘制.
(2) 观察函数的单调性:选中函数图象上的某一点,拖动鼠标左右移动,观察函数值的变化情况,从而判断函数的单调性.
(3) 观察函数的对称性:选择y=x2-2x+3函数图象,点击【变换】中的【反射】,观察函数图象关于直线x=1对称,便可得出函数y=x2-2x+3关于直线x=1对称的结论.
(4) 观察函数的顶点坐标:选中函数图象,选择【测算】菜单中的【坐标】命令,可以得到函数图象的顶点坐标为(1,2),从而得出函数y=x2-2x+3的顶点坐标为(1,2)的结论.
2.3 函数中最值和零点问题的应用
在高中函数教学中,几何画板可以用来探究函数的最值和零点问题.以人教B版教材为例,应用详情如下:
(1) 函数的最值问题:在讲解二次函数的图象和性质时,可以使用几何画板画出函数图象,并拖动图象上的点观察函数的最值,例如:在讲解y=ax2+bx+c(a≠0)的图象时,可以通过改变a、b、c的值观察图象的形状和最值.通过这种方式,学生可以直观地观察到二次函数的顶点坐标和最值,从而更好地理解二次函数的性质[3].
(2) 函数的零点问题:在讲解函数的零点时,可以使用几何画板画出函数图象,并通过拖动图象上的点观察函数的零点,例如:在讲解f(x)=lnx+2x-6的零点时,可以画出函数图象,并拖动图象上的点观察y=0时的x的值.通过这种方式,学生可以直观地观察到函数的零点,从而更好地理解零点的概念和性质.
2.4 函数与其他数学内容的综合应用
在高中函数教学中,几何画板可以用来探究函数与其他数学内容的综合应用.以人教B版教材为例,应用详情如下:
2.4.1 函数与方程的综合应用
在讲解方程的根与函数的零点时,可以使用几何画板画出函数图象,并通过拖动图象上的点观察函数与轴的交点,从而判断方程的根的个数.例如:在讲解函数f(x)=x2-2x-3的零点时,可以使用几何画板画出函数图象,通过观察图象与x轴的交点,可以发现函数有两个零点,分别为x1=-1和x2=3.
2.4.2 函数与不等式的综合应用
在讲解不等式时,可以使用几何画板绘制图象,继而拖动点位便可确定取值范围,从而判断不等式的解集.例如:在讲解函数f(x)=x2-2x+1的不等式f(x)>0的解集时,可以使用几何画板画出函数图象,通过观察图象在x轴上方的部分,可以发现函数的取值范围为f(x)>0,即x≠1.
2.4.3 函数与导数的综合应用
在讲解导数时,可以使用几何画板画出函数图象,并通过拖动图象上的点观察函数的切线,从而判断函数的单调性和极值.例如:在讲解函数f(x)=x3-3x2+3x的导数f(x)=3x2-6x+3的图象时,可以使用几何画板画出函数图象和导数图象,通过观察导数图象的正负性,可以发现函数在x=1处取得极大值.
3 高中数学教学中几何画板的运用建议
3.1 解决实际问题
几何画板可以用于解决一些实际问题,如最优化问题、物理学中的运动问题等.通过绘制函数图象,学生可以更好地理解问题的本质,找到解决问题的方法.例如:在讲解导数的应用时,可以使用几何画板绘制物体的运动轨迹,通过观察导数的变化理解物体的运动状态.
3.2 小组合作学习
在课堂上,可以组织学生进行小组合作学习,共同使用几何画板探究函数的性质和应用,有助于培养学生的合作精神和探究能力.例如:在讲解三角函數的图象和性质时,组织学生分组使用几何画板绘制不同三角函数的图象,并共同探讨三角函数的性质[4].
3.3 比较数值大小
在几何画板中,可以绘制两个函数的图象,通过比较它们在同一自变量处的函数值大小,帮助学生理解函数的大小关系.例如:在讲解指数函数和对数函数的大小关系时,可以使用几何画板绘制y=ax和y=logax的图象,通过比较它们在同一自变量处的函数值大小,让学生理解指数函数和对数函数的大小关系.
3.4 可视化函数
使用几何画板可以绘制各种函数的图象,帮助学生直观地理解函数的形状、单调性、奇偶性等性质.例如:在讲解幂函数的性质时,可以使用几何画板绘制y=x2、y=x3等函数的图象,让学生通过观察图象的变化理解幂函数的单调性和奇偶性.
4 结束语
综上所述,在高中数学教学中,教师应积极运用几何画板,将其与传统教学方法相结合,提高教学效果.同时,教师还应引导学生自主探索和实践,培养学生的数学素养和创新能力.然而,在实际教学中仍然存在一些问题和挑战,需要相关人员不断探索和改进,为高中数学教学的发展做出更大的贡献.
参考文献:
[1] 田素芳.几何画板在高中数学教学中的应用研究[J].小作家选刊(教学交流),2021(26):8-9.
[2] 严江华.几何画板在高中数学教学中的应用[J].中文科技期刊数据库(全文版)教育科学,2022(6):149-151.
[3] 陈艳.几何画板在高中数学教学中运用的探究与分析[J].数学学习与研究,2022(21):125-127.
[4] 朱陈清.几何画板在高中数学教学运用中的探究与分析[J].中文科技期刊数据库(引文版)教育科学,2022(1):71-74.

