谈谈含参函数零点问题的解法

邢罡

含参函数零点问题较为复杂.此类问题中零点的个数、位置、取值等随着参数的变化而变化，需灵活运用方程思想、转化思想、分类讨论思想、数形结合思想来辅助解题.本文以一道题目为例，探讨一下含参函数零点问题的解法.

题目：若对于任意的 a >0，函数 f（x）= x3+ ax2+ bx +1在（-∞，0）上只有1个零点，则实数 b 的取值范围为

該函数式为三次多项式，且其中含有两个参数，较为复杂，需运用方程思想、数形结合法求解.

一、运用方程思想

我们知道，函数 f（x）的零点即为方程 f（x）=0的根.因此，在求解含参函数零点问题时，可根据函数零点的定义，令函数为0，构建方程，通过解方程，或研究方程的根、判别式、根与系数的关系来确定零点的个数、位置、取值范围，从而求得问题的答案.

解法1.设函数 f（x）在区间（-∞，0）上的唯一零点为-t（t >0），

我们运用方程思想，可以将零点问题转化为方程 的根的个数问题，根据方程的根的存在性和取值范围 来讨论方程中参数 a、b、c 的值或范围，并根据韦达定 理来建立关于 a、b、c 的关系式，进而利用基本不等式 求得问题的答案.

二、数形结合

数形结合法是求解含参函数问题的重要方法.在 解题时，需根据关系式的特点构造函数模型.可构造一 个函数，也可构造两个函数，然后根据零点的定义，将 问题转化为函数图象与 x 轴、函数图象之间的交点问 题，结合图形讨论交点的个数、位置、大致范围，即可 快速获得问题的答案.

解法2

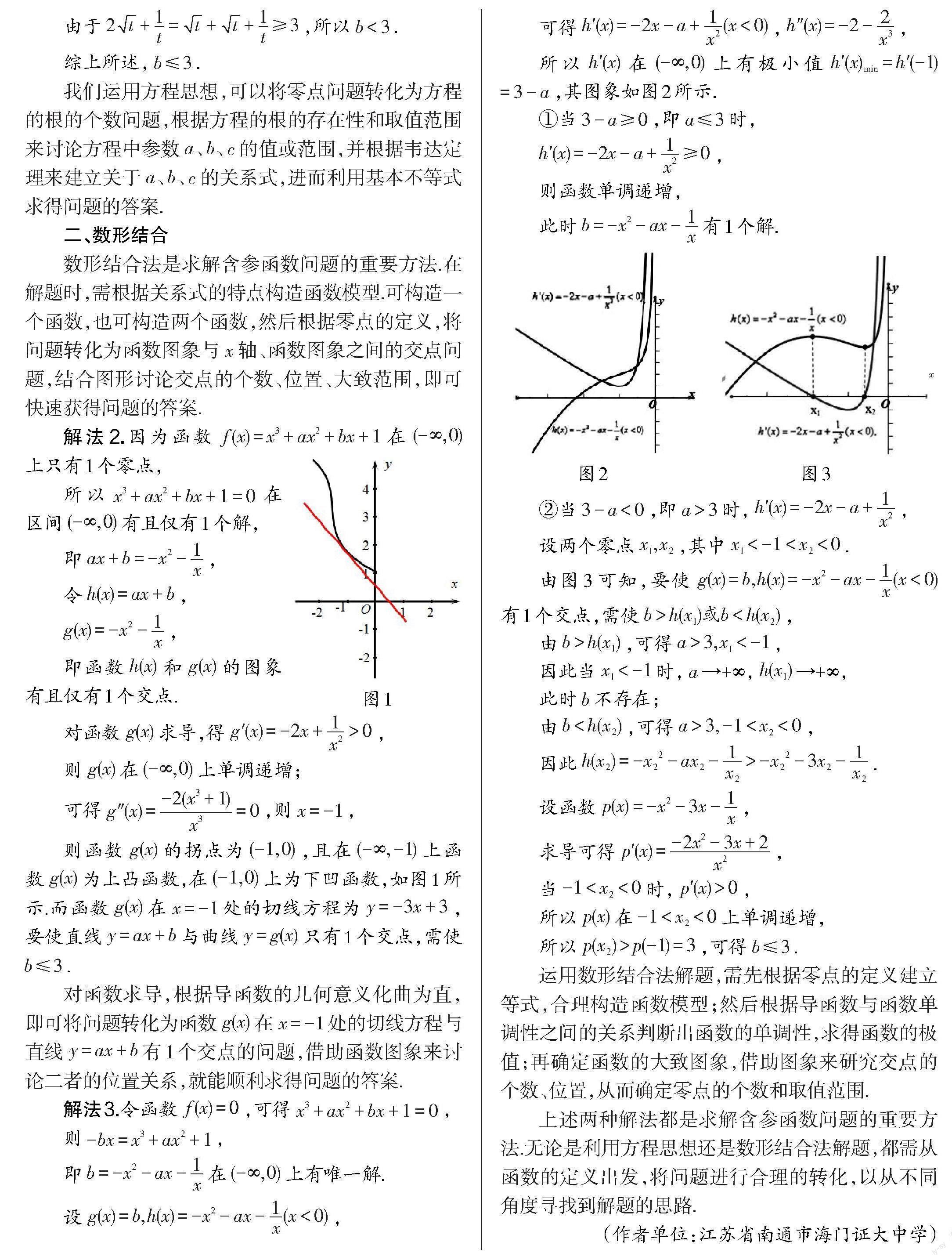
则函数 g（x） 的拐点为 （-1，0） ，且在 （-∞，-1） 上函 数 g（x） 为上凸函数，在 （-1，0） 上为下凹函数，如图1所 示.而函数 g（x） 在 x = -1 处的切线方程为 y = -3x + 3 ， 要使直线 y = ax + b 与曲线 y = g（x） 只有1个交点，需使 b ≤ 3 .

对函数求导，根据导函数的几何意义化曲为直， 即可将问题转化为函数 g（x） 在 x = -1处的切线方程与 直线 y = ax + b 有1个交点的问题，借助函数图象来讨 论二者的位置关系，就能顺利求得问题的答案.

解法3

运用数形结合法解题，需先根据零点的定义建立 等式，合理构造函数模型；然后根据导函数与函数单 调性之间的关系判断出函数的单调性，求得函数的极 值；再确定函数的大致图象，借助图象来研究交点的 个数、位置，从而确定零点的个数和取值范围.

上述两种解法都是求解含参函数问题的重要方 法.无论是利用方程思想还是数形结合法解题，都需从 函数的定义出发，将问题进行合理的转化，以从不同 角度寻找到解题的思路.

（作者单位：江苏省南通市海门证大中学）