深挖教材 提炼方法 培养思维


摘 要:在新课程改革背景下,教育教学的重心从知识传授向综合素质培养转变.培养学生的综合素质,不仅要求学生掌握教材知识内容,同时还要求教师注重学生思维方式的培养.数学作为初中阶段的基础学科,具有比较强的逻辑性,教师应当重视学生问题分析能力的培养,引导学生利用辩证思想,借助分类讨论思想解决问题.据此,文章浅析分类讨论思想在初中数学中的应用.
关键词:分类讨论思想;初中数学;应用策略
中图分类号:G632 文献标识码:A 文章编号:1008-0333(2023)35-0062-03
在初中数学解题中,解题方式较为灵活,一道习题可能会有多种解题方式,不同类型的题目也可能有着相同的解题思路.在数学问题解决中,教师应当注重数学思想的应用.分类讨论思想是重要的数学思想之一,广泛用于学习与生活,可完善学生数学知识体系,锻炼学生思维能力及逻辑能力.同时,借助分类讨论思想,帮助学生整理数学知识点,深入探究数学知识规律,简化数学问题,让学生切实做到举一反三.
1 初中数学教材中分类讨论思想内容分析
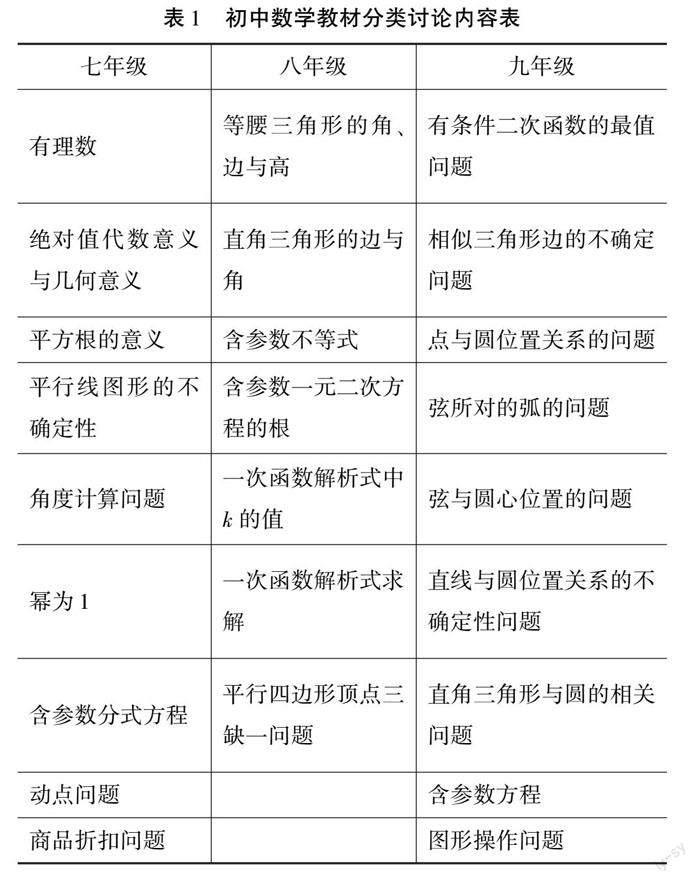
在初中数学教材中,包含很多分类讨论思想内容,要求学生在学习过程中,体会分类讨论思想,做出归纳和总结,以此,完善学生知识结构,体会分类讨论思想在解题中的运用.初中数学各阶段分类讨论思想内容如表1所示.
对于初中阶段的学生来说,刚刚系统化地接触分类讨论思想,想要深入发掘教材中的分类讨论思想,需要了解分类的原则与步骤,尝试自主分类,明确分类思路,为数学问题解决做出知识迁移准备[1].
2分类讨论思想的应用原则
2.1 同一性原则
在初中数学解题中,分类讨论应当坚持同一个标准,对对象做出合理的分类.需要让学生认识到,分类思想应用的前提是有着明确的研究对象,只有准确把握对象特征,才能够灵活利用,围绕同一性进行分类,避免出现不同组对象产生属性交集.
2.2 层次性原则
针对多次分类问题,需要准确把握层次性原则,结合概念的差异做好研究对象分类.在整个分类过程中,应当做到全面考虑,避免忽略对象的某个属性,导致出现分类错误.
3 初中数学解题中分类讨论思想的应用策略
3.1 利用分类讨论思想解决方程问题
例1 某商场准确购进A、B、C三种型号的电视机,A型号电视机每台进价为1 500元,B型号电视机每台进价为2 100元,C型号电视机每台进价为2 500元,如果商场准备使用90 000元购进三种型号的电视机50台,那么进货方案有几种?
分析 通过对题目条件进行分析,利用方程不能够直接得出结果,而且A、B、C三种电视机的数量都是变量,因此,需要对问题进行转化,利用分类讨论思想进行解题.
解 设购进A、B、C三种型号电视机数量分别是x、y、z台,根据题意得出x+y+z=501 500x+2 100y+2 500z=90 000,得出3y+5z=75,即y=25-53z,∵53z为正整数,∴z是3的倍数.
∴5≤53z<25且53z为正整数,∴z的值可能是3、6、9、12.
当z=3时,得出y=20,x=27;
当z=6时,得出y=15,x=29;
当z=9时,得出y=10,x=31;
当z=12时,得出y=5,x=33;
答:商場可以有四种进货方案.
3.2 利用分类讨论思想解决函数问题
函数问题是初中数学中的常见题型,主要有一次函数、反比例函数、二次函数等,作为考试中常见的题型,是初中数学解题中的重点和难点.因此,作为初中数学教师,需要有效利用分类讨论思想,引导学生解决函数问题.
例2 如图1所示,在平面直角坐标系中,抛物线y=ax2+bx的对称轴是x=34,且抛物线经过点A(2,1),点P是抛物线上的动点,横坐标为m(0<m<2),过P点作PB⊥x轴,垂足为B,PB与OA的交点是C,点O关于直线PB的对称点是D,连接CD、AD,过点A作AE⊥x轴,垂足为E.
(1)求解抛物线的解析式;
(2)用含有m的式子表示C、D的坐标;
(3)如果△ACD为等腰三角形,求解所有符合条件的P点坐标.
解 (1)根据题意得-b2a=344a+2b=1,解得a=1b=-32,∴抛物线的解析式为y=x2-32x.
(2)C(m,12m),D(2m,0).
(3)根据题意,得出B(m,0),
在Rt△OBC中,OC2=OB2+BC2=m2+(12m)2=54m2,∴OC=52m,
∵O、D关于直线PC对称,∴CD=OC=52m,
在Rt△AOE中,OA=OE2+AE2=5,
∴AC=OA-OC=5-52m,
在Rt△ADE中,AD2=AE2+DE2=4m2-8m+5.
在P点坐标求解时,可以分三种情况进行讨论.
当AC=CD时,即5-52m=52m,解得m=1,∴P(1,-12);
当AC=AD时,则AC2=AD2,即5-5m+54m2=4m2-8m+5,解得m1=0,m2=1211,
∵0<m<2,∴m=1211,即P(1211,-54121);
当DA=DC时,则DA2=DC2,∴4m2-8m+5=54m2,
解得m1=1011,m2=2,∵0<m<2,∴m=1011,即P(1011,-65121).
综上,当△ACD为等腰三角形时,点P的坐标分别是P1(1,-12)、P2(1211,-54121)、P3(1011,-65121).
3.3 利用分类讨论思想解决几何问题
在初中几何问题教学中,教师可以巧妙引入分类讨论思想,引导学生思考问题,明确解题思路.如直线与圆的位置关系、等边三角形的边角关系以及直角三角形的边角关系等,可以巧妙利用分类讨论思想,完成几何问题的解题.
例3 在Rt△ABC中,∠C=90°,AC=2,BC=4,点D、E分别为BC、AB的中点,将△BDE围绕B点旋转,旋转后D、E的对应点分别是D′、E′,当直线D′E′经过点A时,线段CD′的长是_______.
分析 此题解题时分两种情况,当A点在E′D′的延长线上以及A点在线段D′E′的延长线上,通过分类讨论,求解出BD的长度,完成解题.
解 如图2所示,当A点在E′D′的延长线上时,
∵∠C=90°,AC=2,BC=4,
∴根据勾股定理得出AB=25,
∵点D、E分别为BC、AB的中点,
∴DE∥AC,DE=12AC=1,BD=12BC=2,
∴∠EDB=∠ACB=90°,
∵将△BDE绕着点B旋转,
∴∠BD′E′=∠BDE=90°,D′E′=DE=1,BD=BD′=2,
∵Rt△ABC和Rt△BAD′中,D′B=AC=2,AB=BA,
∴Rt△ABC≌Rt△BAD′,
∴四边形ACBD′为平行四边形,且∠ACB=90°,
∴四边形ACBD′是矩形,
∴CD′=AB=25.
如圖3所示,当点A在线段D′E′的延长线上时,
∵∠AD′B=90°,
∴根据勾股定理得出AD′=4,
∴AE′=AD′-D′E′=3,
∵将△BDE绕着点B旋转,∴∠ABC=∠E′BD′,
∵BE′AB=12=BD′BC,
∴△ABE′∽△CBD′,∴AE′CD′=ABBC,
∴3CD′=254,∴CD′=655.
∴CD′的长度是25或者655.
参考文献:
[1] 关建昌.新课标下初中数学分类讨论思想教学的几个着力点[J].数学学习与研究(教研版),2021(16):12-13.
[责任编辑:李 璟]
收稿日期:2023-09-15
作者简介:陈友杰(1971.11-),男,福建省闽清人,本科,中学一级教师,从事初中数学教学研究.

