《解三角形》专题训练

宋希婷

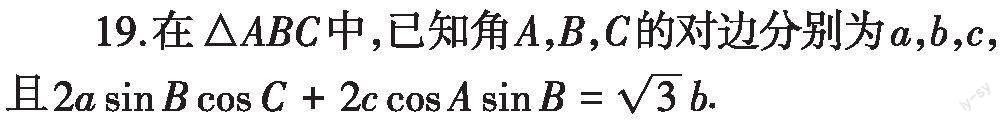
一、单选题

1.设△ABC的内角A，B，C所对的边分别为a，b，c，若bcos C＋ccos B＝asin A，则△ABC的形状为（     ）

A. 锐角三角形 B. 直角三角形

C. 钝角三角形 D. 不确定

二、多选题

9.下列选项中正确的是（     ）

A. [a=30，b=25， A=150°]，有一解

B. [a=7，b=14， A=30°]，有两解

C. [a=6，b=9， A=45°]，有两解

11.对于△ABC，其中正确的判断是（     ）

A. 若cosA＝cosB，则△ABC为等腰三角形

C. 若a＝8，c＝10，B＝60°，则符合条件的△ABC有两个

D. 若sin2A+sin2B＜sin2C，则△ABC是钝角三角形

12.下列结论正确的是（     ）

A.在[△ABC]中，若[A>B]，则[sinA>sinB]

B.在锐角三角形[ABC]中，不等式[b2+c2-a2>0]恒成立

三、填空题

13.在△ABC中，内角A，B，C所对的边分别为a，b，c，已知a＝4，c＝6，C＝2A，则cosA＝________，b＝________.

15.在△ABC中，A，B，C所对的边分别为a，b，c，已知a2＋b2－c2＝ab，且acsin B＝2sin C，则△ABC的面积为________.

四、解答题

（2）若AM为[∠BAC]的平分线，且[AC=1]，求[△ACM]的面积.

（1）求角[B]的大小；

（2）若[△ABC]为锐角三角形，且[c=2a]，[b=1]，求[△ABC]的面积.

参考答案与解析

一、单选题

1.【答案】B

【解析】由正弦定理得sin Bcos C＋sin Ccos B＝sin2A，

∴sin（B＋C）＝sin2A，即sin（π－A）＝sin2A，sin A＝sin2A.

∴△ABC为直角三角形.

2.【答案】B

3.【答案】B

所以[b2=c2+ac]，由余弦定理[b2=a2+c2-2accosB]，

可得[a-2ccosB=c]，

再由正弦定理得[sinA-2sinCcosB=sinC]，

因为[sinA-2sinCcosB=sin（B+C）-2sinCcosB=sin（B-C）]，

所以[sin（B-C）=sinC]，所以[B-C=C]或[B-C+C=π]，

得[B=2C]或[B=π]（舍去）.

因為[ΔABC]是锐角三角形，

二、多选题

9.【答案】AD

故选AD.

10.【答案】AD

故选AD.

11.【答案】ABD

12.【答案】ABC

【解析】对于[A]，在[△ABC]中，若[A>B]，根据大边对大角，所以[a>b]，

由正弦定理得[2RsinA>2RsinB]，

则[sinA>sinB]，故选项[A]正确.

故不等式[b2+c2-a2>0]恒成立，故选项[B]正确.

对于[C]，在[△ABC]中，[a2-c2=bc]，

由余弦定理可知：[a2=b2+c2-2bc?cosA]，

因此[c=b-2c?cosA，得sinC=sinB-2sinC?cosA?sinC=sin（π-A-C）-2sinC?cosA]，

即[sinC=sin（A-C）]，因为[C∈（0，π）]，

所以[sinC=sin（A-C）>0]，

因此[A-C∈（0，π）]，所以[C=A-C]或[C+A-C=π]，

即[2C=A]，或[A=π]（舍去），

故选[ABC].

三、填空题

13.【答案】4或5

四、解答题

17.【解析】（1）[∵c=2bcosB]，由正弦定理可得[sinC=2sinBcosB]，

（2）由题意知[AB=2AC=2]，设[BC=x]，

因为[2AC≤BC]，所以[BC=2]，

因为AM为[∠BAC]的平分线，则[∠BAM=∠CAM]，

（h为底边BC的高）

20.【解析】（1）由已知条件得：[sin2B+sinAsin2B=cosA+cosAcos2Bsin2B]

[=cos[π-（B+C）]+cos[π-（B+C）+2B]]

[=-2cosBcosC]，

所以[（sinB+cosC）cosB=0]，