多视角合理转化，巧妙解决垂直关系

■江苏省高邮市第一中学 王 涛

一、代数运算巧转化

例1如图1,在四棱柱ABCD-A1B1C1D1中,侧 棱A1A⊥底 面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点。证明:B1C1⊥CE。

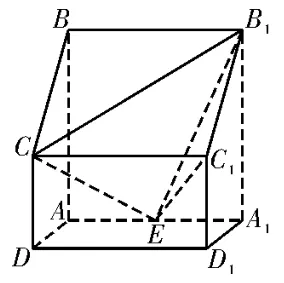
图1

分析:合理选择坐标原点,建立对应的空间直角坐标系,结合条件确定相关点的坐标,得以确定对应直线的方向向量,结合两直线的方向向量的数量积为零来确定两相应的向量垂直,即可证明线线垂直。

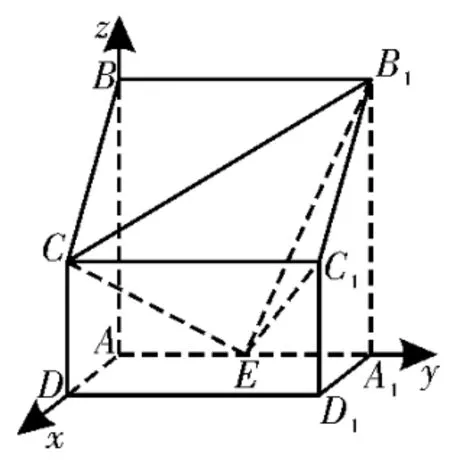
图2

点评:利用代数运算巧妙转化空间垂直关系,往往是借助勾股定理确定线线垂直,借助空间向量的数量积为零确定线线垂直等方式来转化,通过合理的代数运算来达到巧妙转化与证明的目的。

二、推理论证妙证明

例2如图3,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点。求证:

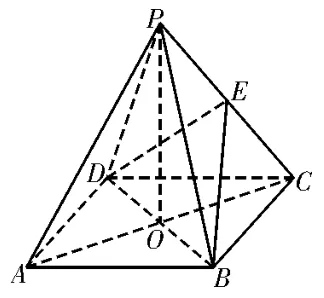
图3

(1)PA∥平面BDE;

(2)平 面PAC⊥平 面BDE。

分析:(1)结合三角形的中位线定理得到线线平行,利用线面平行的判定加以证明线面平行关系;(2)通过线面垂直的性质得到线线垂直,结合线面垂直的判定得以确定线面垂直,再利用面面垂直的判定直接加以推理论证。

where Ceff, CBL, CSi represent the effective front gate oxide capacitance, BL capacitance, and Si channel capacitance.

证明:(1)如图4,AC∩BD=O,连 接OE。在△PAC中,O是AC的 中点,E是PC的中点,则有OE∥AP。又因为OE⊂平面BDE,PA⊄平面BDE,所以PA∥平面BDE。

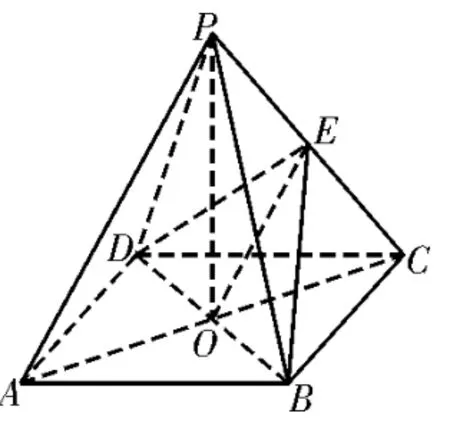
图4

(2)因为PO⊥底面ABCD,BD⊂底面ABCD,所以PO⊥BD。又因为AC⊥BD,且AC∩PO=O,AC⊂平面PAC,PO⊂平面PAC,所以BD⊥平面PAC。又因为BD⊂平面BDE,所以平面PAC⊥平面BDE。

点评:借助逻辑推理中的推理论证来巧妙证明或转化空间垂直关系时,往往先寻找现有直线中是否存在对应平面的垂线,在前面条件不成立的情况下再借助辅助线的构建来分析与解决;如有面面垂直时,一般要用性质定理,在一个平面内作交线的垂线,使之转化为线面垂直,然后进一步转化为线线垂直。

三、代数运算与推理论证相结合

例3如图5,A,B,C,D为空间中的四点。在△ABC中,AB=2,AC=BC=。等边△ADB以AB为轴运动。

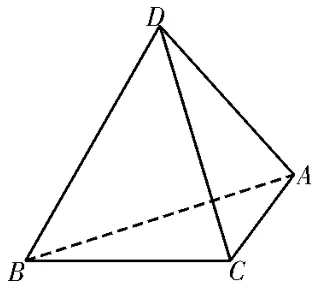
图5

(1)当平面ADB⊥平面ABC时,求线段CD的长度。

(2)当△ADB转动时,是否总有AB⊥CD成立? 证明你的结论。

分析:(1)取AB的中点E,借助等边三角形的性质、面面垂直的性质来确定线面垂直与线线垂直,再结合直角三角形中的代数运算来求解线段的长度;(2)结合转化过程中的不变情形进行分类讨论,综合相应的逻辑推理与应用来证明。

解:(1)如图6,取AB的中点E,连接DE,CE。在等边△ADB中,有DE⊥AB。当平面ADB⊥平面ABC时,由于平面ADB∩平面ABC=AB,则有DE⊥平面ABC,可得DE⊥CE。而在Rt△DEC中,DE=,EC=1,利用勾股定理可得CD=

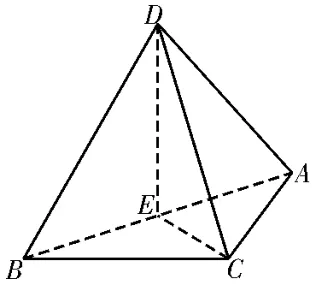
图6

(2)当△ADB以AB为轴转动时,总有AB⊥CD成立。结论证明如下:

①当D在平面ABC内时,由于AC=BC,AD=BD,可知C,D都在线段AB的垂直平分线上,则有AB⊥CD;

②当D不在平面ABC内时,由(1)知DE⊥AB成立,而AC=BC,可得AB⊥CE,又DE,CE为相交直线,所以AB⊥平面CDE,又CD⊂平面CDE,所以AB⊥CD。

综上所述,总有AB⊥CD成立。

点评:在判定空间垂直关系的问题中,代数运算与逻辑推理论证相结合是最常见的技巧方法之一,或代数运算,或推理论证,按需推进,两者有机结合,齐心协力,共达目的,演绎完美的转化过程。

四、创设情境妙创新

例4如图7,在三棱锥P-ABC中,PA=BC=3,PC=AB=5,AC=4,PB=。

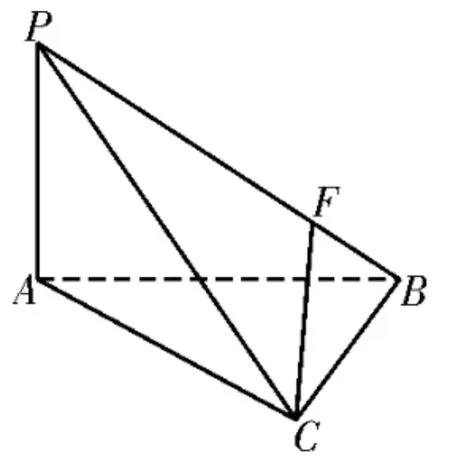
图7

(1)求 证:PA⊥平 面ABC。

(2)过C作CF⊥PB于点F,试问:在线段AB上是否存在一点E,使得PB⊥平面CEF成立? 若存在,求线段BE的长;若不存在,请说明理由。

分析:(1)利用线段长度,结合代数运算,并利用勾股定理转化线段之间的垂直关系,进而利用线面垂直的判定定理来证明;(2)先假设点E的存在性满足线面垂直,通过逻辑推理,借助线面垂直转化为线线垂直,并设出对应线段的长度,利用代数运算合理转化并求解对应线段的长度,进而得以判断存在性问题。

解:(1)由已知得PC2=PA2+AC2=25,PB2=PA2+AB2=34,所以PA⊥AC,PA⊥AB。又AB∩AC=A,所以PA⊥平面ABC。

(2)假设在线段AB上存在一点E,使得PB⊥平面CEF。

因为CE⊂平面CEF,所以PB⊥CE。因为PA⊥平面ABC,所以PA⊥CE。又PA∩PB=P,所以CE⊥平面PAB。因为AB⊂平面PAB,所以CE⊥AB。设BE=x,因为AB2=AC2+BC2,所以∠ACB=90°,所以BC2=BE·AB,即32=5x,解得x=

故在AB上存在点E满足题意,且BE=

点评:以存在性问题来创新设置情境,利用代数运算与逻辑推理的综合与应用,结合线线垂直、线面垂直等之间的关系与转化,实现空间垂直关系的创新应用,得以确定立体几何中的存在性问题。

空间垂直关系的巧妙转化是立体几何化归与转化思想的一个重要方面,充分融合空间中线线垂直、线面垂直与面面垂直的判定、性质等相关知识,融会贯通,合理转化,在学习与应用过程中要加以不断理解和掌握,能有效地培养空间想象力,提升逻辑推理与数学运算等核心素养,提高解决立体几何问题的能力。