证明与求解并重推理与运算齐飞——“立体几何”解答题复习

■陕西省礼泉县教研室 陈银会

立体几何是高考解答题的必考内容,试题主要考查立体几何的基础知识、基本方法和基本思想。通过空间直线、平面位置关系的论证,考查空间想象能力和推理论证能力。通过度量问题的计算,考查逻辑推理能力和运算求解能力。近年来,立体几何在命题设计上不断创新,本文结合最新的模考试题介绍立体几何命题趋势,供同学们复习备考。

考向一、空间几何体中的位置关系及度量问题

空间点、线、面的位置关系通常以空间几何体为载体考查平行、垂直关系的证明,一般出现在解答题的第(1)问,解答题的第(2)问常考查求空间角、体积、距离问题。求解时可以用“综合法”“向量法”,在具体解题时不一定只运用一种方法,可以灵活选用,视情况而定。一般地,对于线面位置关系的“平行”与“垂直”的证明,可以选用“综合法”直接处理,而对于空间角的有关计算,一般采用“向量法”更为方便与快捷。

例1(2022年咸阳市高三月考)如图1,平面ABCD⊥平 面DBNM,且菱形ABCD与菱形DBNM全 等,∠MDB=∠DAB,G为MC的中点。

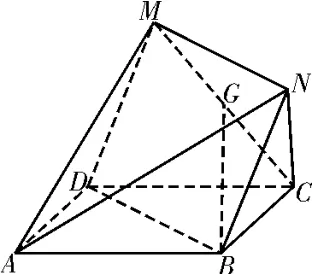
图1

(1)求证:平面GBD∥平面AMN。

(2)求直线AD与平面AMN所成角的正弦值。

解析:(1)如图2,连接AC交DB于E,连接GE,在△AMC中,G,E分别是CM,CA的中点,所以GE∥AM。因为GE⊄平面AMN,AM⊂平 面AMN,所 以GE∥平 面AMN。在菱形DBNM中,MN∥BE,同理可证BE∥平面AMN。又因为BE∩GE=E,所以平面GBD∥平面AMN。

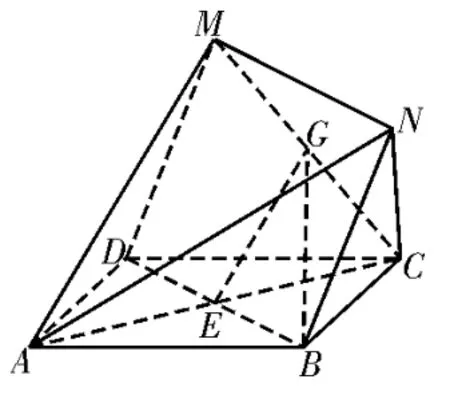
图2

(2)连接ME,因为菱形ABCD与菱形DBNM全等且∠MDB=∠DAB,所以AD=AB=BD,DM=BD=MB,所 以ME⊥BD。又平面ABCD⊥平面MNBD且相交于BD,所以ME⊥平面ABCD。

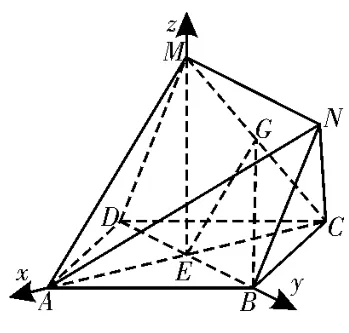
图3

提醒:平行、垂直关系的证明,需要以空间直线、平面的位置关系为基础,建立和形成以公理、定义、判定、性质为主线的立体几何基础知识体系。“空间向量”的引入,给我们处理立体几何问题提供了一种新的视角与更加有效的工具。用向量法解题的思路主要是:(1)分析问题中的关键要素;(2)用向量表示相关要素;(3)进行向量运算求得向量的结果;(4)将向量结果翻译成几何结论。在平常练习中,应多尝试从不同角度解决立体几何问题,积累解题经验,这样在考试中结合自身优势灵活选择解题路径,提升解题效率。

考向二、平面图形折叠成空间几何体的问题

先将平面图形折叠成空间几何体,再以其为载体研究其中的线面之间的位置关系,以及与计算有关的几何量是近几年高考考查立体几何的一类重要考向,它很好地将平面图形拓展成空间图形,同时也为空间立体图形向平面图形转化提供了具体形象的途径,是高考考查空间想象能力的主要方向。

例2(2022年南京市高三月考)图4是由正方形ABCD,Rt△ABE,Rt△CDF组成的一个等腰梯形,其中AB=2。将△ABE,△CDF分别沿AB,CD折起,使得E与F重合,如图5。

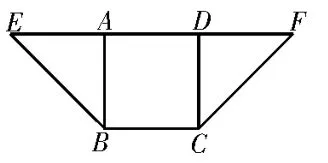
图4

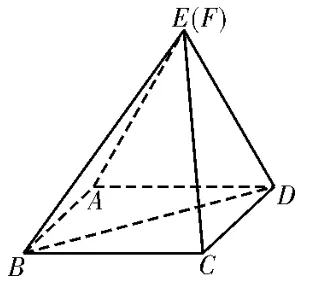
图5

(1)设平面ABE∩平面CDE=l,证明:l∥CD;

(2)若二面角A-BE-D的余弦值为,求AE的长。

解析:(1)因为CD∥AB,AB在平面ABE内,CD⊄平面ABE,所以CD∥平面ABE。又CD⊂平面ECD,平面ABE∩ 平面ECD=l,所以l∥CD。

(2)因为AB∥CD,CD⊥DE,所以AB⊥DE。又AB⊥AE,DE∩AE=E,AE⊂平面ADE,DE⊂平面ADE,所以AB⊥平面ADE。因为AB在平面ABCD内,所以平面ABCD⊥平面AED。过E作EO⊥AD于点O,则O是AD的中点。因为平面ABCD∩平面AED=AD,EO⊂平面ADE,所以EO⊥平面ABCD。

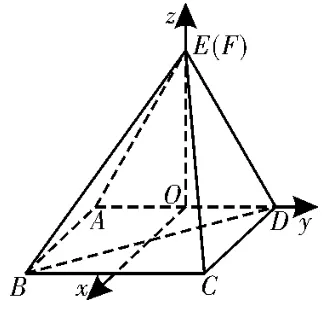
图6

提醒:解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量。一般情况下,长度是不变量,而位置关系往往会发生变化,抓住不变量是解决问题的突破口。解决翻折问题的步骤:第一步,确定折叠前后各量之间的关系,搞清折叠前后的变化量和不变量;第二步,在折叠后的图形中确定线和面的位置关系,明确需要用到的线面;第三步,利用判定定理或性质定理进行证明。

考向三、线、面位置关系中的探索性问题

是否存在某点或某参数,使得某种线、面位置关系成立问题,是近几年高考命题的热点,常在解答题的最后一问中出现,解决这类问题的基本思路类似于反证法,即“在假设存在的前提下通过推理论证,如果能找到符合要求的点(或其他的问题),就肯定这个结论;如果在推理论证中出现矛盾,就说明假设不成立,从而否定这个结论”。

例3(2022年湖北省重点中学联考)如图7,等边△ABC的边长为3,D,E分别是AB,BC上的点,且满足。如图8,将△ADE沿DE折起到△A1DE的位置,使得二面角A1-DE-B成直二面角,连接A1B,A1C。

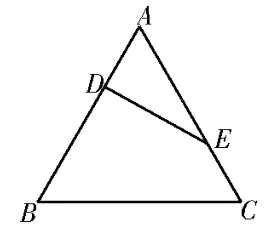
图7

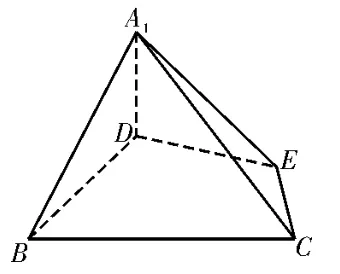
图8

(1)求证:A1D⊥平面BCED。

(2)在线段BC上是否存在点P,使得直线PA1与平面A1BD所成的角为60°? 若存在,求出PB的长;若不存在,请说明理由。

解析:(1)在图7 中,由题得AE=2,AD=1,∠A=60°,在△ADE中,由余弦定理得DE==,故AD2+DE2=AE2,所以AD⊥DE,BD⊥DE。

在图8 中,A1D⊥DE,BD⊥DE,所 以∠A1DB为二面角A1-DE-B的平面角,又二面角A1-DE-B为直二面角,所以∠A1DB=90°,故A1D⊥DB。因为DE∩DB=D,且DE,DB在平面BCED内,所以A1D⊥平面BCED。

(2)由(1)可知ED⊥DB,A1D⊥平面BCDE。

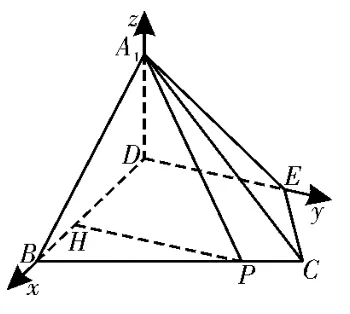
图9

提醒:立体几何中的探究性问题主要有两类:一类是探究线面的位置关系;另一类是探究线面角或二面角满足特定要求时的存在性问题。处理原则是:先建立空间直角坐标系,引入参数(有些是题中已给出),设出关键点的坐标,然后探究这样的点是否存在,或参数是否满足要求,从而作出判断。

近年来高考数学对立体几何部分试题命制,仍以考查主干知识和基本方法为主,难度适中。复习备考中,应以扎实掌握基本立体图形的结构特征为基础,夯实“平行、垂直”的推理论证能力,提升“空间角、距离”等运算的水平。养成良好的规范书写习惯,达到精准、高效突破解答题的目的。