立体几何线面关系的证明易错题剖析

■河南省信阳市固始县信合外国语高级中学 胡云兵

易错点1.证明直线与平面平行时,忽略直线是否在平面内,而造成错误

例1(2023 届四川省广安市高三阶段性测试)如图1,在四棱锥P-ABCD中,四边形ABCD是矩形,AB=,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,E,F分别为PC,PB的中点。证明:EF∥平面PAD。

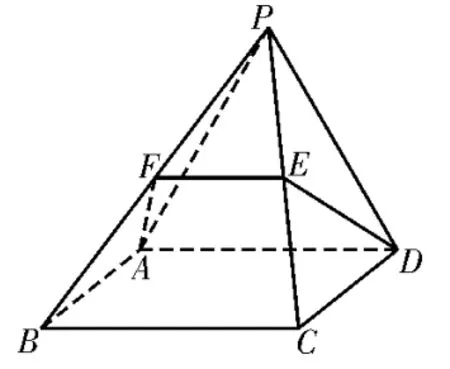
图1

常见错解:因为E,F分别为PC,PB的中点,所以EF∥BC。因为AD∥BC,所以EF∥AD,所以EF∥平面PAD。

错因分析:证明过程中,在说明EF∥AD时,一定要写明“AD⊂平面PAD,EF⊄平面PAD”这两句话,证明过程才完整。

正解:因为E,F分别为PC,PB的中点,所以EF∥BC。因为四边形ABCD是矩形,所以AD∥BC,所以EF∥AD。因为AD⊂平面PAD,EF⊄平面PAD,所以EF∥平面PAD。

易错点2.证明面面平行时缺少线线相交的条件

例2(2023届华大新联盟11月高三质检)如图2,在直三棱柱ABC-A1B1C1中,AB=AC,∠CAB=45°,M为线段A1B与AB1的交点,P,Q分别为线段CC1,AB的中点,延长B1B至点D,使得BD=B1B,连接CD,QD,CQ。求 证:平 面CDQ∥平 面A1BP。

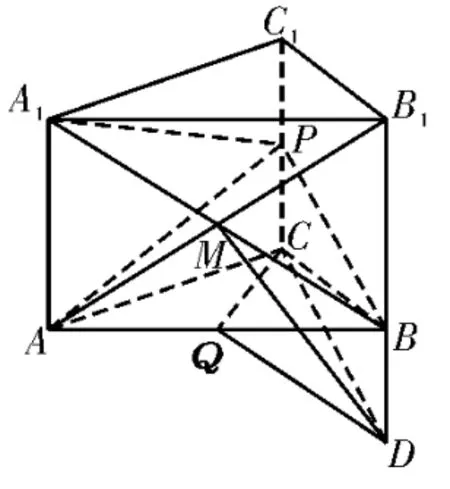
图2

常见错解:连接MQ,因为BD=CP=C1C=B1B,所以CP=BD。又CP∥BD,所以四边形BDCP是平行四边形,则CD∥BP。因为CD⊄平面ABP,BP⊂平面ABP,故CD∥平面ABP。同理可证QD∥平面ABP。CD⊂平面CDQ,QD⊂平面CDQ,所以平面CDQ∥平面ABP。

错因分析:证明过程中,缺少“CD∩QD=D”这个条件,有可能面面相交,逻辑证明不严谨,导致证明过程不完整。

正解:连接MQ,因为BD=B1B,CPB1B,所以CP=BD。又CP∥BD,所以四边形BDCP是平行四边形,则CD∥BP。因为CD⊄平面ABP,BP⊂平面ABP,故CD∥平面ABP。同理可证QD∥平面ABP。因为CD∩QD=D,CD⊂平面CDQ,QD⊂平面CDQ,所以平面CDQ∥平面ABP。

易错点3.证明线面垂直时缺少线线相交的条件

例3(2023 届重庆市西南大学附属中学11 月期中质检)如图3,在四棱锥P-ABCD中,平面PBD⊥平面ABCD,底面ABCD是梯形,AD∥BC,BD⊥PC,AD=AB。证明:BD⊥平面PCD。

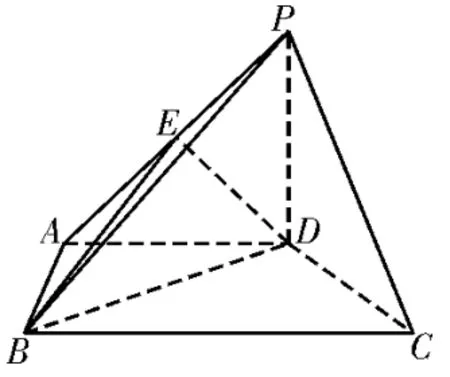
图3

常见错解:取BC的中点F,连接AF,DF。因为AD∥BC,AD=AB=BC,所以四边形ABFD为菱形,四边形AFCD为平行四边形,所以AF⊥BD,AF∥CD,所以CD⊥BD。又BD⊥PC,所 以BD⊥平 面PCD。

错因分析:证明过程中,缺少“CD∩PC=C”这个条件,线面有可能相交但不垂直,逻辑证明不严谨,导致证明过程不完整。

正解:取BC的中点F,连接AF,DF。因为AD∥BC,AD=AB=BC,所以四边形ABFD为菱形,四边形AFCD为平行四边形,所以AF⊥BD,AF∥CD,所以CD⊥BD。又因为BD⊥PC,CD∩PC=C,所以BD⊥平面PCD。

易错点4.证明面面垂直时缺少线在平面内的条件

例4(2023届江西省景德镇市高三第一次质检)如图4,在正三棱锥ABCA1B1C1中,E,F分别是棱AA1,CC1上的点,CM∥平面BEF,且M是AB的中点。证明:平面BEF⊥平面ABB1A1。

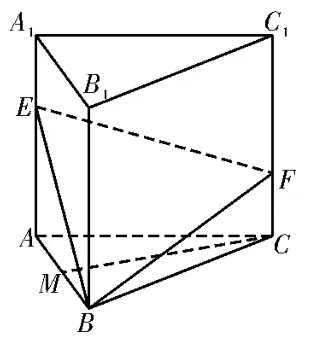
图4

常见错解:因为M是AB的中点且△ABC为等边三角形,所以CM⊥AB。因为AA1⊥平面ABC,所以AA1⊥CM,所以CM⊥平面ABB1A1。因为CM∥平面BEF,所以存在直线l∥CM,所以l⊥平面ABB1A1,所以平面BEF⊥平面ABB1A1。

错因分析:证明过程中,缺少直线l⊂平面BEF的条件,证明过程不完整。

正解:因为M是AB的中点且△ABC为等边三角形,所以CM⊥AB。因为AA1⊥平面ABC,所以AA1⊥CM,所 以CM⊥平面ABB1A1。因为CM∥平面BEF,所以存在直线l⊂平面BEF,所以l∥CM,所以l⊥平面ABB1A1。因为直线l⊂平面BEF,所以平面BEF⊥平面ABB1A1。