立体几何中空间角的易错题剖析
■河南省信阳市固始县信合外国语高级中学 殷武娟
易错点1.忽略异面直线所成角的范围
例1(2023 年四川省宜宾市第三中学校高二期中(理))如图1所示,在直三棱柱ABC-A′B′C′中,AC=BC=AA′,∠ACB=120°,E为BB′的中点,则异面直线CE与C′A所成角的余弦值为( )。
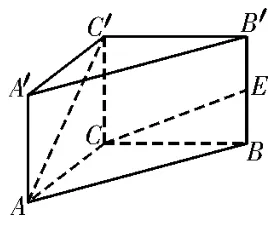
图1
错解:选A。如图2 所示,直三棱柱ABC-A′B′C′向上方补形为直三棱柱ABCA″B″C″,其中A′,B′,C′分别为各棱的中点,取B′B″的中点D′,可知CE∥C′D′,异面直线CE与C′A所成角即为C′D′与C′A所成角。设CB=2,则C′D′=,C′A=2,AD′=,所以cos∠AC′D′=
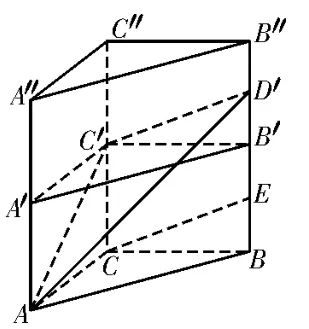
图2
易错点2.混淆线面角和平面的法向量与直线方向向量夹角的关系致错
例2(2023届百师联盟高三上学期11月份联考)如图3,在四棱锥P-ABCD中,底面ABCD是矩形,O为BC的中点,PB=PC=,PD=BC=2AB=2。
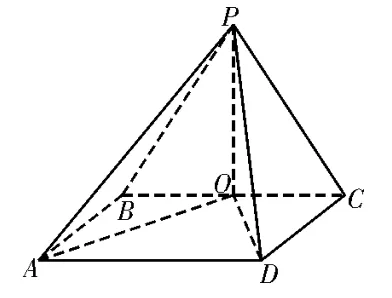
图3
(1)求证:平面PBC⊥平面ABCD。
(2)求直线AD与平面PCD所成角的正弦值。
错解:(1)证明过程略。
(2)由(1)知,PO⊥平面ABCD,取AD的中点Q,连接OQ,易知OQ,OC,OP两两互相垂直。
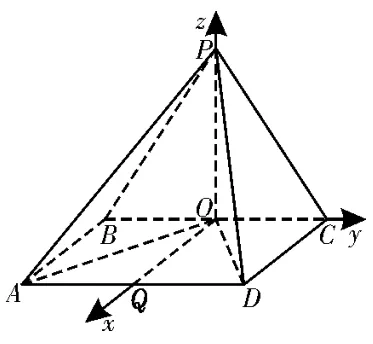
图4
易错点3.忽略两平面法向量的夹角与二面角平面角的关系致错
例3(2023 届吉林省长春市高三上学期11 月份一模)如图5所示的几何体是由棱台ABC-A1B1C1和棱锥DAA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2 的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=B1C1=1。求二面角A1-BDC1的余弦值。

图5
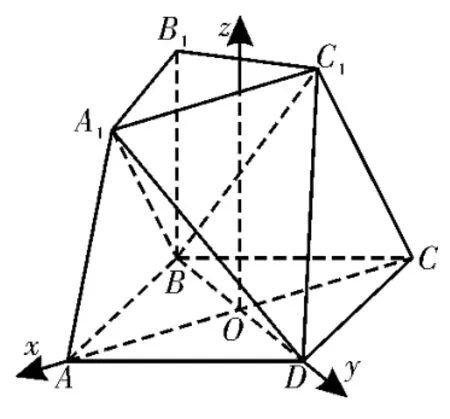
图6
错因分析:错解中误认为两平面法向量的夹角就等于二面角的平面角,实际上二面角的平面角大小是向量n1与n2的夹角(或其补角)。
正解:前面同错解。
由图可知二面角A1-BD-C1为锐角,故二面角A1-BD-C1的余弦值为
易错点4.混淆直线与平面的夹角和二面角的平面角致错

图7

图8
错因分析:错解中误认为两平面法向量的夹角的余弦值等于二面角的平面角的正弦值,混淆线面角和二面角的求法。
正解:(2)前面同错解。

