矩阵方程AX=B的谱范数约束解

刘喜富, 罗 乐

(重庆师范大学 数学科学学院, 重庆 401331)

1 引言与预备知识

EA=Im-AA+,FA=In-A+A.

对于任意的ξ>0,Sveξ(A)表示的是A的奇异值中大于或等于ξ的个数.对于任意矩阵W,W是压缩矩阵当且仅当‖W‖2≤1,W是Hermitian压缩矩阵当且仅当‖W‖2≤1并且W=W*.

约束矩阵方程的求解在矩阵理论和其他很多领域中都起着重要的作用.近些年,约束线性矩阵方程AX=B的求解问题一直是研究的热门问题之一,这些约束主要包括：Hermitian、(半)正定、(反)自反、中心对称、范数等.矩阵方程AX=B约束解的结论在振动理论及其逆问题、结构化设计、统计和控制理论等领域有着广泛的应用,近年来诸多学者都对其有了很深的研究：文献[1-2]利用矩阵的广义逆给出了线性矩阵方程AX=B存在一般解的充要条件及解的表达式;Li等[3]给出了矩阵方程AX=B的解在特殊情况下关于秩的结论;Liu等[4]研究了矩阵方程AX=B的Hermitian解和半正定解在保范扩张下的应用;王婧等[5]研究了矩阵方程AX=B的(反)自反问题以及最佳逼近问题;Zhang等[6]利用矩阵的分解研究了矩阵方程的P、Q的(反)自反解问题;Sou等[7]给出了问题

‖A-BXC‖2<1

最小秩解的一般形式.

当矩阵方程

AX=B

(1)

分别存在一般解、Hermitian解、半正定解时,本文主要考虑该矩阵方程在2种谱范数约束下的解,即最小谱范数解，以及谱范数小于1的解.

问题 1给定矩阵A∈Cm×l,B∈Cm×k,求相容矩阵方程AX=B在以上2种约束条件下的一般解.

问题 2给定矩阵A∈Cm×l,B∈Cm×l,求相容矩阵方程AX=B在以上2种约束条件下的Hermitian解.

问题 3给定矩阵A∈Cm×l,B∈Cm×l,求相容矩阵方程AX=B在以上2种约束条件下的半正定解.

为了得到以上问题的解,引入以下引理.

引理 1.1[5]1) 给定矩阵A∈Cm×l,B∈Cm×k,矩阵方程AX=B相容的充要条件为AA+B=B.有解时,该方程的一般解可以表示为X=A+B+FAY,其中Y是适当阶数的任意矩阵.

2) 给定矩阵A∈Cm×l,B∈Cm×l,相容矩阵方程AX=B存在Hermitian解的充要条件为BA*是Hermitian矩阵.有Hermitian解时,该方程的Hermitian解可以表示为

X=A+B+FA(A+B)*+FAYFA,

其中Y是适当阶数的任意Hermitian矩阵.

3) 给定矩阵A∈Cm×l，B∈Cm×l,相容矩阵方程AX=B存在半正定解的充要条件为BA*是半正定矩阵,且r(BA*)=r(B).有半正定解时,该方程的半正定解可以表示为

X=B*(BA*)+B+FAYFA,

其中Y是适当阶数的任意半正定矩阵.

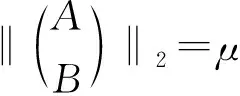
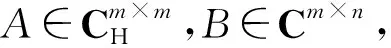
其中

是适当阶数的任意Hermitian压缩矩阵.

设矩阵A∈Cm×n的奇异值分解为

V*、U、V都是酉矩阵,其中

Λ1=diag(σ1,σ2,…,σk),
Λ2=diag(σk+1,σk+2,…σl),
σ1≥σ2≥…≥σk≥1>σk+1≥…≥σl>0,r(A)=l,

则可定义

引理 1.4[4]给定矩阵A∈Cm×n,B∈Cm×mx,C∈Cnx×n,其中B是列满秩矩阵,C是行满秩矩阵,B、C的奇异值分解为

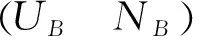
X=

其中

并且

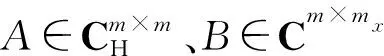
‖A-BXB*‖2<1.

引理 1.5[9]给定矩阵A∈Cm×m,B∈Cm×n,C∈Cn×n,D∈Cn×m,设A、C是可逆矩阵,则A+BCD可逆的充要条件为C-1+DA-1B可逆,此时它的逆可表示为

(A+BCD)-1=

A-1-A-1B(C-1+DA-1B)-1DA-1.

引理 1.6[10]给定矩阵

其中A、D是Hermitian矩阵,则M>0的充要条件为A>0,D-B*A+B>0.

2 问题1的解

给定矩阵A∈Cm×l,B∈Cm×k,A的奇异值分解为

(2)

其中U、V都是酉矩阵,Σ=diag(σ1,σ2,…,σr),
σ1≥σ2≥…≥σr>0, r(A)=r.

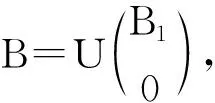
(3)

其中X2为适当阶数的任意矩阵.

定理 2.1给定A∈Cm×l,B∈Cm×k,相容矩阵方程(1)的解如(3)式所示,该方程的最小谱范数解可表示为

A+B+FAY,

(4)

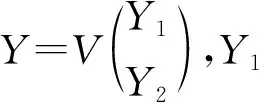
K为适当阶数的任意压缩矩阵.

证明由引理1.2可得(4)式成立,即

μ=min‖X‖2=‖Σ-1B1‖2=‖A+B‖2.

定理 2.2给定A∈Cm×l,B∈Cm×k,相容矩阵方程(1)的解如(3)式所示,该方程存在谱范数小于1的解的充要条件为‖A+B‖2<1.该方程有约束解时,它的一个约束解为

(5)

证明AX=B的解如(3)式所示,它的谱范数可转化为

其中

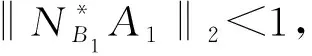
‖A+B‖2<1.

方程(1)有约束解时,则

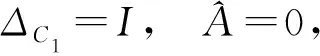
故方程(1)的一个谱范数小于1的解为(5)式.

给定矩阵

A=

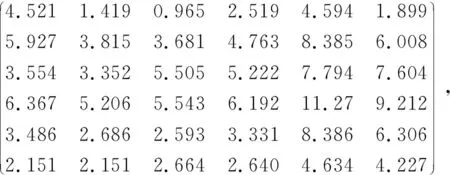
B=

例 2.1矩阵方程(1)解的最小谱范数为μ=0.795,此时它的最小谱范数解如(4)式所示：

X=A+B+FAY,

其中

例 2.1矩阵方程(1)的谱范数小于1的一个解如(5)式所示,即可表示为

3 问题2的解

给定矩阵A∈Cm×l,B∈Cm×l,A的奇异值分解如(2)式所示.由引理1.1可得,矩阵方程(1)存在Hermitian解时,B可以相应的表示为

且该方程的Hermitian解可以表示为

(6)

其中X22是适当阶数的任意的Hermitian矩阵.

定理 3.1给定矩阵A∈Cm×l,B∈Cm×l,矩阵方程(1)的Hermitian解如(6)式所示,该方程的Hermitian最小谱范数解可表示为

A+B+FA(A+B)*+FAYFA,

(7)

其中

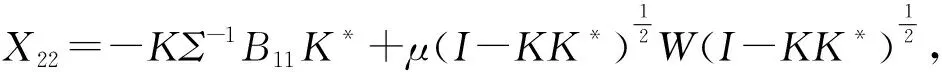
W是适当阶数的任意Hermitian压缩矩阵.

证明由引理1.3易证(7)式成立,即

定理 3.2给定矩阵A∈Cm×l,B∈Cm×l,矩阵方程(1)的Hermitian解如(6)式所示,方程存在谱范数小于1的Hermitian解的充要条件为‖A+B‖2<1,该方程有Hermitian约束解时,它的一个约束解可以表达为

A+B+FA(A+B)*+FAYFA，

(8)

其中Y如定理3.1所示,则

(9)

证明AX=B的Hermitian解如(6)式所示,它的谱范数可转化为

其中

,

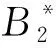
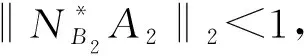
方程(1)有约束解时,由引理1.4和引理1.5可得：

再次应用引理1.4可得(9)式及矩阵方程(1)的一个谱范数小于1的Hermitian解为(8)式.

给定矩阵

A=

B=

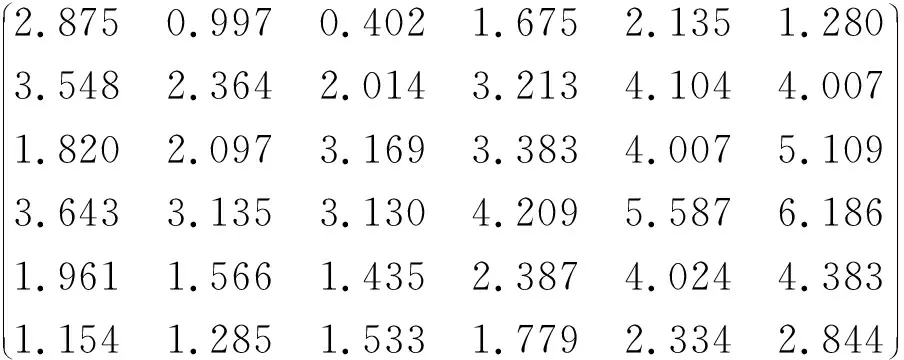
例 3.1矩阵方程(1)解的最小谱范数为μ=0.717,此时它的最小谱范数解如(7)式所示,即

X=A+B+FA(A+B)*+FAYFA,

其中FA、V*如例2.1所示.

例 3.2矩阵方程(1)的谱范数小于1的解如(8)式所示,即

X=A+B+FA(A+B)*+FAYFA,

其中FA如例2.1所示,A+B+FA(A+B)*如例3.1所示，即

即

4 问题3的解

给定矩阵A∈Cm×l,B∈Cm×l,A的奇异值分解如(2)式所示.由引理1.1可得,矩阵方程(1)存在半正定解时,B可以相应的表示为

且方程(1)的半正定解可表示为

X=

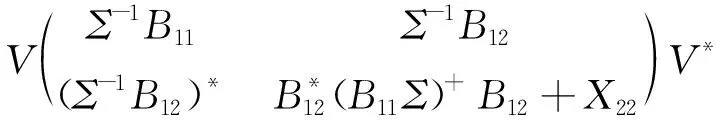
(10)

其中X22是适当阶数的任意半正定矩阵.

定理 4.1给定矩阵A∈Cm×l,B∈Cm×l,矩阵方程(1)的半正定解如(10)式所示,该方程的一个最小谱范数半正定解可表示为

B*(BA*)+B.

(11)

证明AX=B的半正定解如(10)式所示.由于

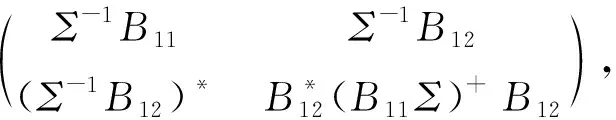
X22是任意的半正定矩阵,故可得

由偏序的性质可得

‖X‖2=

取X22=0时上式等式成立.此时,矩阵方程(1)的一个半正定最小谱范数解为(11)式.

值得注意的是,定理4.1的证明并未使用保范扩张定理,这是因为在(10)式中不能保证存在半正定矩阵X22使得

当等式成立时,可通过保范扩张定理结合半正定矩阵的性质得到通解.

定理 4.2给定矩阵

A∈Cm×l,B∈Cm×l,

矩阵方程(1)的半正定解如(10)式所示,该方程存在谱范数小于1的半正定解的充要条件为

‖B*(BA*)+B‖2<1.

该方程有谱范数小于1的半正定解时,它的解可表示为

X=

B*(BA*)+B+FAYFA,

(12)

其中Y如定理3.1所示,即

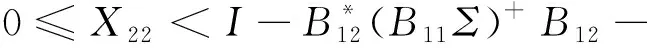
证明AX=B的半正定解如(10)式所示.由定理4.1可得

min‖X‖2≥

‖B*(BA*)+B‖2,

即方程(1)存在谱范数小于1的半正定解的充要条件为‖B*(BA*)+B‖2<1.有解时,由偏序的性质可得

显然I-Σ-1B11>0,则由引理1.6可得

(Σ-1B12)*(I-Σ-1B11)+Σ-1B12>0,

即

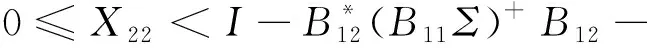
值得注意的是,不同于定理2.2和定理3.2,定理4.2没有利用引理1.4进行求解问题.

实际上引理1.4可适用于该问题的求解,但由于得出结果为X22=0,结果显然,且证明过程冗杂,故引理1.4利用偏序予以证明.

给定矩阵

A=

B=

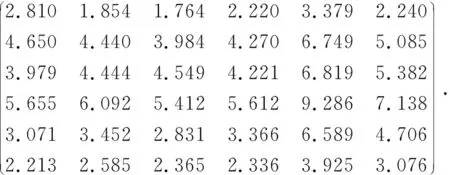
例 4.1矩阵方程(1)解的最小谱范数为μ=0.895,此时它的最小谱范数解如(10)式所示,即

例 4.2矩阵方程(1)的谱范数小于1的解为

X=B*(BA*)+B+FAYFA,

其中FA、V*如例2.1所示,B*(BA*)+B如例4.1所示,即

5 结束语

对于谱范数约束条件‖X‖2<1,在实际应用中,常遇到约束条件：对于任意的ξ(ξ>0),则

‖X‖2<ξ.

实际上,本文的结论也同样适用于该约束：对于矩阵方程AX=B,令

则AX=B可转化为AξXξ=B,则