公理化模糊集合的特征及其分类
张 波, 潘小东, 谢健祥
(西南交通大学 数学学院, 四川 成都 611756)
Zadeh[1]在1965年引入了“模糊集合”的概念,旨在建立一种描述和处理模糊信息的数学理论和方法.模糊集合的基本思路是在绝对真(通常用1表示)和绝对假(通常用0表示)之间增加额外的真值来刻画事物之间的差异所存在的中介过渡过程,即通过定义一个从非空论域U到[0,1](后来被推广到格[2]、区间值[3]等其他结构)的函数(称为隶属函数)来描述模糊概念(如:青年、高个子等)的外延.经过50多年的研究与发展,模糊集合理论在理论与应用2个方面都取得了长足的进步,目前已经被广泛应用于诸如人工智能、聚类分析、模式识别、决策等领域[4-17].
对于模糊集合的理论和应用而言,一个重要而基本的问题是:如何确定它的隶属函数?对此,文献[7]认为:“模糊现象的特征是进一步发展模糊逻辑及其应用的根本……模糊现象在模糊逻辑的起源中扮演着关键角色.”文献[8]认为:“模糊性的本质的研究是对人类智力的挑战.这方面的任何一点突破都将极大地推动智能系统的研究,同时也将深化目前意义下的模糊性理论.”基于对模糊现象的深入分析,文献[9]认为:“模糊现象是反映事物的质变和量变之间差异的一种现象,模糊性是在对事物进行定性分析的时候,事物的质和量之间所表现出来的差异特性.”基于这样的认识,文献[9]给出了隶属度的公理系统,并基于模糊划分的概念给出了模糊集合的公理化定义.公理化模糊集合理论是对经典模糊集合理论的严格化、明确化,这在一定程度上解决了模糊集合理论中长期存在的关于隶属函数的合理性问题,为模糊集合在理论和应用方面的进一步发展奠定了坚实的理论基础.
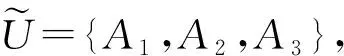
1 预备知识
首先介绍文中使用到的一些记号以及三角模、三角余模和强否定算子.
定义 1.1[10]一个三角模(简称t模)T指的是一个定义在[0,1]闭区间上的二元运算T,即一个二元函数T:[0,1]2→[0,1],使得对任意的x,y,z∈[0,1],满足以下4条公理:
(T1)T(x,y)=T(y,x);
(T2)T(T(x,y),z)=T(x,T(y,z));
(T3)T(x,y)≤T(x,z),当y≤z;
(T4)T(x,1)=x.
定义 1.2[10]一个三角余模(简称t余模)S指的是一个定义在[0,1]闭区间上的二元运算S,即一个二元函数S:[0,1]2→[0,1],使得对任意的x,y,z∈[0,1],满足(T1~T3)以及
(S4)S(x,0)=x.
本文中记三角模取小为⊗M,记三角余模取大为⊕M.
定义 1.3[11](否定、严格否定和强否定) (i) 称一个不增的函数N:[0,1]→[0,1]为否定,如果:
(N1)N(0)=1,N(1)=0.
(ii) 称一个否定N:[0,1]→[0,1]为严格否定,如果还满足:
(N2)N是连续的.
(N3)N是严格单调递减的.
(iii) 称一个严格否定N:[0,1]→[0,1]为强否定,如果它还是对合的,即
(N4)N∘N=id[0,1]是连续的.
显然,N:[0,1]→[0,1]是一个严格否定当且仅当它是严格单调递减的双射.
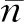
定义 1.4[11](模糊划分) 设U=[a,b]⊂R,U上的一个模糊划分是具有如下形式的对象
其中
Ai={(x,μAi(x))|x∈U},i=1,2,…,n,
函数μAi:U→[0,1]定义了元素x∈U关于类Ai(代表某种质,即定性描述的类)的隶属度,并且满足下面的条件:
μAi(x0)=1;
μAi(x0)=1,
那么,μAi(x)在[a,x0]上不减,在[x0,b]上不增;
4) 对任意的x∈U,有
0<μA1(x)+μA2(x)+…+μAn(x)≤1.
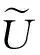
基于模糊划分,下面给出模糊集合的公理化定义.
定义 1.5[11](公理化模糊集合) 设
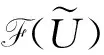
μA(x)=μAi(x)
对所有x∈U都成立,那么
2) 如果μA(x)=1对所有x∈U都成立,那么
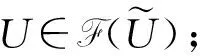
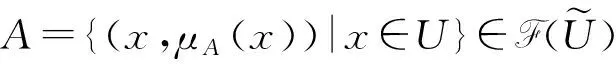
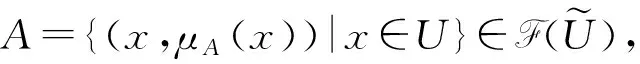
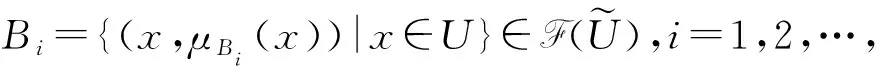
B1∩⊗B2∩⊗…∩⊗Bn∩⊗…=
B1∪⊕B2∪⊕…∪⊕Bn∪⊕…=
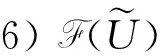
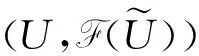
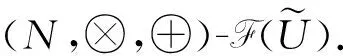
2 公理化模糊集合的规范形式

例如,在正则模糊划分
下,取强否N为N(x)=1-x,设
B(x)=1-A2(x)=(A2(x))N,
虽然A1和B表面上并不相同,实际上却是一致的.那么,在公理化模糊集中,怎么判断表面上不一样而实际上是相等的2个模糊集呢?
命题 2.1设
A={(x,μA(x))|x∈U},B={(x,μB(x))|x∈U}∈
则
(A∩⊗MB)r=Ar∩⊗MBr,(A∪⊕MB)r=Ar∪⊕MBr.
证明任取x∈U,若A(x)≥B(x),则
(A∩⊗MB)r(x)=
(A(x)⊗MB(x))r=(B(x))r.
又因为r∈R+,故
(A(x))r≥(B(x))r,
那么
(Ar∩⊗MBr)(x)=
(A(x))r⊗M(B(x))r=(B(x))r,
故
(A∩⊗MB)r=Ar∩⊗MBr.
A(x) 采取相同的办法可以证明∪⊕M与语气算子也可交换,即 (A∪⊕MB)r=Ar∪⊕MBr. 因为取小⊗M、取大⊕M之间是有分配律的,故∩⊗M、∪⊕M之间也有分配律,即下面命题成立. 命题 2.2设 则: (A∪⊕MB)∩⊗MC=(A∩⊗MC)∪⊕M(B∩⊗MC), (A∩⊗MB)∪⊕MC=(A∪⊕MC)∩⊗M(B∪⊕MC). 称定义1.5中3)对应的生成模糊集的方式为A经过了一次语气运算. 定义 2.3由有限个简单模糊集构成的模交式称作模交模糊集,由有限个简单模糊集构成的模并式称作模并模糊集. A=(A1)N∩⊗(A2)2,B=A2∪⊕((A1)N)3, 则A是模交模糊集,B是模并模糊集. 定义 2.4由有限个模交模糊集构成的模并式称作模并模糊集范式,由有限个模并模糊集构成的模交式称作模交模糊集范式. A=(A1∩⊗(A2)2)∪⊕((A2)N∩⊗(A1)2),B=((A1)N∪⊕A2)∩⊗((A2)3∪⊕A1), 则A是模并模糊集范式,B是模交模糊集范式. 证明当A=U或者A=∅时,规范形式已经约定好,命题成立;否则,A是由模糊划分中的元素生成的,此时可以按照如下的步骤找到A的规范形式.有以下恒等关系: (A∩⊗MB)r=Ar∩⊗MBr, (1) (A∪⊕MB)r=Ar∪⊕MBr, (2) (A∩⊗MB)N=AN∪⊕MBN, (3) (A∪⊕MB)N=AN∩⊗MBN, (4) (A∪⊕MB)∩⊗MC=(A∩⊗MC)∪⊕M(B∩⊗MC), (5) (A∩⊗MB)∪⊕MC= (A∪⊕MC)∩⊗M(B∪⊕MC). (6) 根据(1)~(6)式,可以按以下步骤找到定理中的模交模糊集范式和模并模糊集范式. 第1步 利用(1)~(4)式可以把模糊集A变换成B1,使得B1是由简单模糊集经∪⊕M、∩⊗M运算生成,并且A与B1是相等的. 第2步 根据(5)式可以把B1变换为B2,但B2中∩⊗M的作用范围内不出现∪⊕M,并且B2与B1相等,显然B2就是定理中所要求的模并模糊集范式. 经过类似于上述的步骤,但在第2步中使用(6)式,就得到定理中所要求的模交模糊集范式. A=((A1∩⊗MA2)3∪⊕MA3)N 的规范形式. 解使用(4)式得 A=((A1∩⊗MA2)3)N∩⊗M(A3)N, 使用(1)式得 A=((A1)3∩⊗M(A2)3)N∩⊗M(A3)N, 使用(3)式得 A=(((A1)3)N∪⊕M((A2)3)N)∩⊗M(A3)N, (7) 使用(5)式得 A=(((A1)3)N∩⊗M(A3)N)∪⊕M (((A2)3)N∩⊗M(A3)N). (8) (7)式为与模糊集A相等的模交模糊集范式,(8)式为与模糊集A相等的模并模糊集范式. 基于公理化模糊集合的规范形式,下面研究公理化模糊集合的特征和性质.由前面的定义可知下面的结论成立. 命题 3.11) 模并(交)模糊集范式在x0处的隶属度为0(1),当且仅当构成该模并(交)模糊集范式的每个模交(并)模糊集在x0处的隶属度为0(1); 2) 模并(交)模糊集范式在x0处的隶属度为1(0),当且仅当构成该模并(交)模糊集范式的模交(并)模糊集中至少存在一个模交(并)模糊集,它在x0处的隶属度为1(0); 3) 模交(并)模糊集在x0处的隶属度为1(0),当且仅当构成该模交(并)模糊集的每一个简单模糊集在x0处的隶属度均为1(0); 4) 模交(并)模糊集在x0处隶属度为0(1),当且仅当构成该模交(并)模糊集的简单模糊集中至少存在一个简单模糊集,它在x0处隶属度取值为0(1). 这里只证明1),其余的结论可类似说明. A=B1∪⊕MB2∪⊕M…∪⊕MBl,l∈N+, 其中Bi均为模交模糊集.若A(x0)=0,则 (B1∪⊕MB2∪⊕M…∪⊕MBl)(x0)=0, 即 B1(x0)⊕MB2(x0)⊕M…⊕MBl(x0)=0, 从而 B1(x0)=B2(x0)=…=Bl(x0)=0, 所以说它的每个模交模糊集在x0处取值为0.上述证明反过来也成立,从而原命题成立.A(x0)=1时类似可证. 证明因为A是模交模糊集,所以设 A=B1∩⊗MB2∩⊗M…∩⊗MBl,l∈N+, 其中Bi,i∈{1,2,…,l}是简单模糊集. 由模糊集核的定义可知Aj(x)=1,由模糊划分定义1.4的条件4) 0<μA1(x)+μA2(x)+…+μAn(x)≤1, 可知 Ai(x)=0,i≠j, 所以模糊划分中元素在x处取值为0或1;又因为Bi是简单模糊集,不妨假设Bi是由模糊划分中元素Ak生成的,注意到Ak(x)=1或0.结合简单模糊集的定义可知,简单模糊集Bi(x)=0或1,i∈{1,2,…,l},从而 A(x)=B1(x)⊗MB2(x)⊗M…⊗MBl(x)=0或1. 证明考虑AN.因为A是模并模糊集,则AN是模交模糊集.根据命题3.2可知AN(x)=0或1,由强否定的性质知A(x)=(AN(x))N=1或0. 在这些结论的基础之上可以得到下面的定理. 证明如果A=U或者∅,结论显然成立. 根据定理2.1,不妨设 A=B1∪⊕MB2∪⊕M…∪⊕MBk,k∈N+, 其中Bi,i∈{1,2,…,k}均是模交模糊集. 由命题3.2知Bi(x0),i∈{1,2,…,k}取值为0或1,故 A(x0)=B1(x0)⊕MB2(x0)⊕M…⊕MBk(x0)=0或1. 容易发现,若A∈C0,则AN∈C1;若B∈C1,则BN∈C0;若C∈C2,则CN∈C2.3类元素关于语气算子均是封闭的.下面讨论∩⊗M、∪⊕M下,3类元素的运算问题,首先讨论∩⊗M下同类模糊集之间的运算. 1)A∩⊗MB∈C0,∀A,B∈C0; 2)A∩⊗MB∈C1,∀A,B∈C1; 3)A∩⊗MB∉C1,∀A,B∈C2. 证明1) 任取A,B∈C0,则 则 (A∩⊗MB)(x1)=A(x1)⊗MB(x1)=0⊗M0=0, 所以 A∩⊗MB∈C0. A(x1)=B(x1)=1, 那么 (A∩⊗MB)(x1)=A(x1)⊗MB(x1)=1⊗M1=1, 从而 A∩⊗MB∈C1. (A∩⊗MB)(x1)=A(x1)⊗MB(x1)= 0⊗MB(x1)=0, 从而 A∩⊗MB∉C1. C2中任意元素与自身做∩⊗M运算属于C2.下面举例说明C2与C2中元素做运算可能属于C0. 关于∩⊗M下不同类间元素的运算,有如下结论. 1)A∩⊗MB∈C0,∀A∈C0,B∈C1; 2)A∩⊗MB∈C0,∀A∈C0,B∈C2; 3)A∩⊗MB∈C2,∀A∈C1,B∈C2. 证明1) 任取A∈C0,B∈C1,则 都有 A(x0)=0,B(x0)=1, 那么 (A∩⊗MB)(x0)=A(x0)⊗MB(x0)=0⊗M1=0, 所以 A∩⊗MB∈C0. 2) 任取A∈C0,B∈C2,则对 都有A(x0)=0,那么 (A∩⊗MB)(x0)=A(x0)⊗MB(x0)= 0⊗MB(x0)=0, 所以 A∩⊗MB∈C0. B(x0)=1,B(x1)=0. 又因为A∈C1,所以 A(x0)=A(x1)=1, 从而 (A∩⊗MB)(x0)=A(x0)⊗MB(x0)=1⊗M1=1,(A∩⊗MB)(x1)=A(x1)⊗MB(x1)=1⊗M0=0, 故A∩⊗MB∈C2. 类似地,关于∪⊕M运算有如下性质. 1)A∪⊕MB∈C0,∀A,B∈C0; 2)A∪⊕MB∈C1,∀A,B∈C1; 3)A∪⊕MB∉C0,∀A,B∈C2. 证明1) 任取A,B∈C0,则AN,BN∈C1,那么由命题3.4中2)可知 (A∪⊕MB)N=AN∩⊗MBN∈C1, 从而A∪⊕MB=((A∪⊕MB)N)N∈C0. 2) 任取A,B∈C1,则AN,BN∈C0,那么由命题3.4中1)可知 (A∪⊕MB)N=AN∩⊗MBN∈C0, 从而A∪⊕MB=((A∪⊕MB)N)N∈C1. (A∪⊕MB)(x1)=A(x1)⊕MB(x1)= 1⊕MB(x1)=1, 从而A∪⊕MB∉C0. 下面举例说明C2与C2中元素做∪⊕M运算可能属于C1. {(x,(-x+1)⊕Mx|x∈U}∈C1. 1)A∪⊕MB∈C1,∀A∈C0,B∈C1; 2)A∪⊕MB∈C2,∀A∈C0,B∈C2; 3)A∪⊕MB∈C1,∀A∈C1,B∈C2. 证明1) 任取A∈C0,B∈C1,则 AN∈C1,BN∈C0, 那么由命题3.5中1)可知 (A∪⊕MB)N=AN∩⊗MBN∈C0, 从而A∪⊕MB∈C1. 2) 任取A∈C0,B∈C2,则 AN∈C1,BN∈C2, 那么由命题3.5中3)可知 (A∪⊕MB)N=AN∩⊗MBN∈C2, 从而A∪⊕MB∈C2. 3) 任取A∈C1,B∈C2,则 AN∈C0,BN∈C2, 那么由命题3.5中2)可知 (A∪⊕MB)N=AN∩⊗MBN∈C0, 从而A∪⊕MB∈C1. 本文定义了公理化模糊集合的2种规范形式,证明了(N,⊗M,⊕M)型公理化模糊集合的规范形式存在定理.基于规范形式证明了(N,⊗M,⊕M)型公理化模糊集合中元素的特征,并给出了模糊集的 分类.这些成果对进一步研究公理化模糊集合的数学性质、模糊隶属空间的结构和性质具有重要的理论和实践意义.本文研究的是带Zadeh算子和强否定算子的公理化模糊集合,一般情形下的公理化模糊集合的规范形式和特征还需要进一步的研究;这将是今后努力的方向.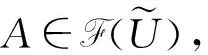
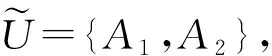

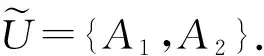
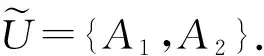

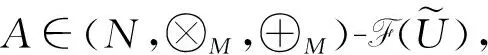
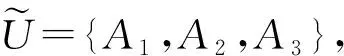
3 公理化模糊集合的特征及分类



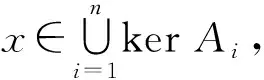

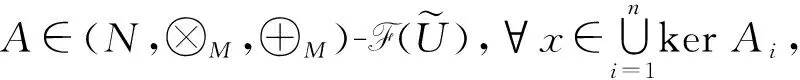

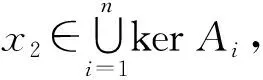

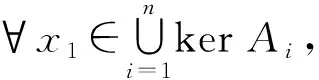
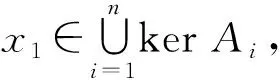
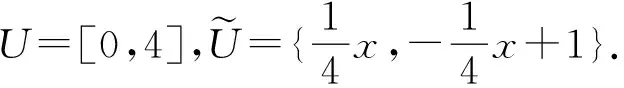

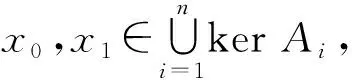

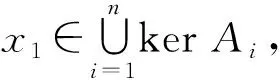
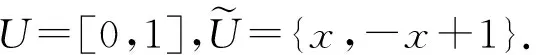

4 结束语

