广义色散方程的李群分析、最优系统、对称约化及精确解

胡彦鑫, 郭增鑫, 辛祥鹏

(聊城大学 数学科学学院, 山东 聊城 252000)

在非线性波以及孤立子理论的相关物理问题中,色散方程占据着相当重要的位置,它是解决波传播问题的方程.根据色散方程能够得到宏观上波传播的速度,例如波峰移动的速度.色散方程在流体力学研究中起着重要的作用,在面对许多复杂的物理问题时,人们通常会将其转化为偏微分方程的求解问题[1].因此,对于如何构造偏微分方程的精确解逐渐成为物理和数学等学科诸多学者研究的重要问题.随着时间的推移,求解偏微分方程的方法也越来越多,例如，经典李群方法[2]、F-展开法[3]、椭圆函数展开法[4]、试探函数法[5]和双曲函数展开法[6]等.

考虑如下形式的五阶色散方程

ut+αuxuxx+βuxxxxx+γux=0,

(1)

其中,u=u(x,t),α、β、γ为任意常数.方程(1)已有许多研究者采用不同的方法进行了深入探讨,如:2009年宋国亮等[7]采用试探函数法求出方程(1)在γ=0时的孤波解和有理解等；文献[8-9]采用(G′/G)展开法构造了方程(1)特殊形式的多个行波解,并且讨论了ux在不同次幂下的该色散方程解的情况,最终得出该方程的行波解.本文在已有研究的基础上对方程增加一项色散控制项,使得方程在不失去物理意义的前提下能够模拟更多的传播现象.同时，从李群方法入手,结合多种辅助函数展开法构造了方程(1)的孤子解和三角函数解等.

1 方程(1)的对称

设方程(1)的向量场为

(2)

其中ξ(x,t,u)、τ(x,t,u)、φ(x,t,u)是未知函数.若向量场(2)为方程(1)的李点对称,就要满足

pr(5)V(Δ)|Δ=0=0,

(3)

其中

Δ=ut+αuxuxx+βuxxxxx+γux,

可以得到方程(1)的五阶延拓为

pr(5)V=φt+φx(αφxx+γ)+βφxxxxx=0,

(4)

(4)式中的φt、φx、φxx、φxxxxx是由(2)式中的ξ(x,t,u)、τ(x,t,u)、φ(x,t,u)的微分项决定:

φt=Dt(φ-ξux-τut)+ξuxt+τutt,

(5)

φx=Dx(φ-ξux-τut)+ξuxx+τuxt,

(6)

φxx=Dxx(φ-ξux-τut)+ξuxxx+τuxxt,

(7)

φxxxxx=Dxxxxx(φ-ξux-τut)+

ξuxxxxxx+τuxxxxxt,

(8)

这里(5)～(8)式中的Dx、Dt是关于t、x的全微分算子.

将(5)～(8)式代入(4)式,由对称的相关条件,令包含u的各阶导数的系数均等于零,可得到关于ξ、τ、φ的决定方程组,求解后可得方程(1)的李点对称

(9)

其中，C1、C2、C3、C4为任意常数.

接下来对上述对称进行分类讨论:

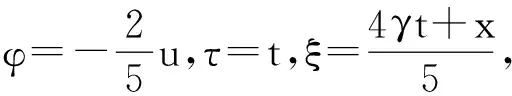
(10)

2) 当C2=1,C1=C3=C4=0时,φ=0,τ=1,ξ=0,代入(2)式,得到

(11)

3) 当C3=1,C1=C2=C4=0时,φ=1,τ=0,ξ=0,代入(2)式,得到

(12)

4) 当C4=1,C1=C2=C3=0时,φ=0,τ=0,ξ=1,代入(2)式,得到

(13)

综上,得到了方程(1)的4个李点对称.

下面将利用这4个基本对称构造出方程(1)的一维最优系统,并利用对称将方程(1)转化为常微分方程.

2 李代数与最优系统

前面已求出的4个方程(1)的李点对称向量场为

(14)

接下来进行最优系统的计算.首先由李括号[10]运算定义

[Vi,Vj]=ViVj-VjVi,

得到李代数交换子表(如表1所示).

表 1 李代数交换子表

再由李代数伴随[11]表达式

得到李代数伴随作用表(如表2所示).

表 2 李代数伴随表

接下来进行最优系统的构造.首先假设由向量场Vi(i=1,2,3,4)构成如下的李代数L4:

V=a1V1+a2V2+a3V3+a4V4,

其中a1、a2、a3、a4是任意常数.构造最优系统的目的是利用伴随作用尽可能多的消掉ai(i=1,2,3,4),使得V的表达式尽可能简单.

a1V1+a2V2+a3V3+a4V4-ε[a1[V2,V1]+

a2[V2,V2]+a3[V2,V3]]+a4[V2,V4]]-…=

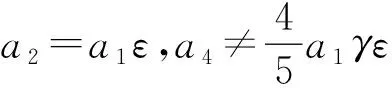
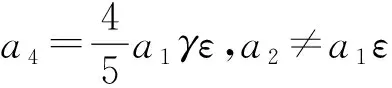
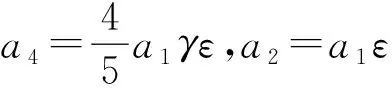
a1V1+a2V2+a3V3+a4V4-ε[a1[V3,V1]+

a2[V3,V2]+a3[V3,V3]]+a4[V3,V4]]-…=

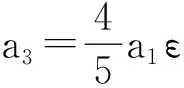
a1V1+a2V2+a3V3+a4V4-ε[a1[V4,V1]+

a2[V4,V2]+a3[V4,V3]]+a4[V4,V4]]-…=

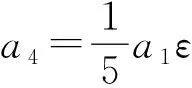
综上,得到方程(1)的一维最优系统为

{V1,V2,V3,V1+λ1V3,V1+λ2V3+λ3V4,

V1+λ4V2+λ5V3,V1+λ6V2+λ7V4},

其中λi(i=1,2,…,7)是任意常数.

3 对称约化

对称约化是一种较为实用的约化方法.下面将会利用所求得的向量场对方程(1)进行对称约化,从而可使方程(1)转化为常微分方程.接下来基于第1部分的4个李点对称,对方程(1)进行对称约化.

1) 对于向量场

其对应的特征方程为

由特征方程得到不变量ξ1,并且由

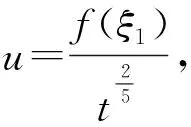
(15)

αf′f″+βf‴″+γf′=0．

(16)

f′=0．

(17)

-qf′+αf′f″+βf‴″+γf′=0.

(18)

至此完成了对于方程(1)的约化.

4 方程(1)的精确解

接下来将对第3部分中约化的结果进行精确解的构造,在这里选取(16)和(18)式,但是(16)式的形式其实是(18)式中-q=0时的特殊形式,因此将选取更具有一般性的(18)式进行求解.(18)式中f是关于ξ4的函数,其中ξ4=x-qt,这里的q为任意常数,对(18)式关于变量ξ4积分得

(19)

其中C为任意常数,取C=0.

1) 假设方程(19)有如下形式的解

(20)

这里的ω=ω(ξ4),并且满足方程

ω″+λω′+μω=0,

(21)

这里的αm、λ、μ是任意常数.由齐次平衡原理得

2(m+1)=m+4,

故m=2,则方程有如下形式的解

(22)

将(21)和(22)式代入方程(19)得

2αμ2α1α2+22βλ2μα1+120βλμ2α2+

βλ3μα1+14βλ2μ2α2+8βλμ2α1-

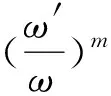
(23)

把(23)式代入(22)式,当λ2-4μ>0时,方程(19)的精确解为

f1(ξ4)=

则方程(1)的精确解为

u1(x,t)=

当λ2-4μ=0时,方程(19)的精确解为

则方程(1)的精确解为

u2(x,t)=

当λ2-4μ<0时,方程(19)的精确解为

f3(ξ4)=

则方程(1)的精确解为

u3(x,t)=

其中

ξ4=x-qt,

q=βλ4-8βλ2μ+16βμ2+γ,

C1、C2、β、γ为任意常数.

至此,完成了第一种辅助函数展开法对于方程(1)精确解的构造,接下来将采用另一种辅助函数展开法对方程(1)进行研究.

2) 假设方程(19)有如下形式的解

(24)

其中ω=ω(ξ4),并且满足方程

ω2-ω′+δ=0,

(25)

这里的αm、δ是任意常数.由齐次平衡原理m=2,则方程有如下形式的解

(26)

将(25)和(26)式代入方程(19)得

136βδ2a2-4αa-2a2-αa-1a1-qa2+γa2)ω2+

16βδ2a-1+2αa-2a-1-qa-1+γa-1)+

(2αδ2a1a2-4αδa-1a2+16βδ2a1-2αα-2a1-qa1+

提取ωm的系数得到超定方程组,求解可以得到α-2、α-1、α0、α1、α1,q的值,选取以下2种情况:

(27)

(28)

(Ⅰ) 把(27)式代入(26)式,当δ>0时,方程(19)的精确解为

则方程(1)的精确解为

当δ<0时,方程(1)的精确解为

其中

ξ4=x-qt,q=16βδ2+γ,

C3、β、γ为任意常数.

(Ⅱ) 把(28)式代入(26)式,当δ>0时,方程(19)精确解为

则方程(1)的精确解为

当δ<0时,方程(1)精确解为

u7(x,t)=

其中

ξ4=x-qt,q=256βδ2+γ,

C4、β、γ为任意常数.

5 结束语

利用李群对一类广义五阶色散方程进行研究,求出方程的对称,构建了一维李代数的最优系统,得到约化方程,并采用2种辅助函数展开法得到方程的一系列不同的精确解,丰富了方程的精确解的种类,具有一定的理论意义,该研究方法可以应用于其他的非线性发展方程.