关于共形向量场的Ricci平均值及应用
何 雅,吴元芬
(云南师范大学 数学学院,云南 昆明 650500)
1 主要定理
共形向量场是微分几何中的一个必不可少的组成部分. 若流形M上的一个向量场ξ所诱导的局部单参数可微变换群是共形变换群, 则称向量场ξ是M上的一个共形向量场, 下面给出共形向量场的定义[1].
设ξ为黎曼流形(Mn,g)上的光滑切向量场, 如果在M上存在一个光滑函数ρ满足:
则称ξ为共形向量场, 其中Lξ是度量g关于ξ的李导数,ρ为共形向量场ξ的势函数. 特别地, 当ρ为零时,ξ称为Killing向量场[2], 其诱导的局部单参数可微变换群是等距变换群. 若ξ是闭的向量场, 那么ξ称为闭的共形向量场; 若ξ是某个光滑函数的梯度向量场,ξ则称为共形梯度向量场.
许多作者[3-4]研究了具有常纯量曲率, 且存在共形向量场的黎曼流形在一定的条件下等距于欧氏空间中的球, 而黎曼流形上存在共形梯度向量场在文献[5—6]中已被研究. 本文主要考虑共形向量场的Ricci平均值, 下面给出Ricci平均值的定义.
设(Mn,g)是n维黎曼流形,M上的一个光滑向量场X的Ricci平均值定义为:
其中V为M的体积,Ric为M上的Ricci张量.
在文献[7]中, Yano等证明了如下定理.
定理1设(Mn,g)(n≥2)是一个紧定向的黎曼流形,Ric为M上的Ricci张量, 若M上的共形向量场ξ满足Ric(ξ,ξ)≤0, 则ξ必为平行向量场, 且Ric(ξ,ξ)=0当且仅当ξ是Killing向量场.
然而, 该定理没有给出Ric(ξ,ξ)=0时流形的分类, 因此, 本文在较弱的假设条件下给出了流形的分类, 于是得到了下面的结果.
定理2设(Mn,g)(n≥2)是一个紧定向的黎曼流形, 若Mn上存在非零的共形向量场ξ, 则关于ξ的Ricci平均值δ(ξ)≥0. 特别地, 当δ(ξ)=0时,Mn等距于黎曼积Γ×Mn-1, 其中dim Γ=1.
2 预备知识
本文运用活动标架法进行计算, 并采用Einstein求和约定(重复指标表示求和). 设(M,g)是n维黎曼流形, {e1,…,en}是局部单位正交标架场, {ω1,…,ωn}是对偶向量场, 规定指标范围1≤i,j,k,l≤n, 则M的结构方程为:
dωi=ωj∧ωji,ωij+ωji=0,
(1)
(2)
其中d为M上的外微分算子,ωij与Rijkl分别为黎曼度量g诱导的联络形式与黎曼曲率.
下面定义Ricci曲率和纯量曲率:

显然Ricci曲率关于i,j是对称的.
设向量场ξ∈X(M), 则ξ在单位正交标架场下的表达式为:
ξ=ξiei.
向量场ξ∈X(M)的一阶、 二阶协变导数分别定义为:
ξi,jωj=dξi+ξjωji,
(3)
ξi,jkωk=dξi,j+ξk,jωki+ξi,kωkj.
(4)
对(3)式两边外微分, 并由结构方程及(3)式与(4)式得向量场ξ∈X(M)的Ricci恒等式为:
ξi,jk-ξi,kj=ξlRlijk.
向量场ξ∈X(M)的散度定义为:
div(ξ)=ξi,i,
则ξ为共形向量场当且仅当
(5)
显然,ρ=div(ξ).
向量场ξ为Killing向量场当且仅当ξi,j+ξj,i=0, 向量场ξ为平行向量场当且仅当▽ξ=0, 即ξi,j=0. 显然平行向量场为Killing向量场.
对(5)式两边同时求协变导数, 有:
(6)
由(6)式有:
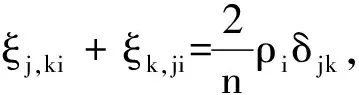
(7)
(8)
结合(6)式、 (7)式和(8)式有:
由ξ的Ricci恒等式有:
通过第一Bianchi恒等式, 上式为:
(9)
3 定理2的证明
在证明定理2之前, 先证明如下引理.
引理1设(Mn,g)(n≥2)是一个紧定向的黎曼流形, 若Mn上存在非零的共形向量场ξ, 则关于ξ的Ricci平均值δ(ξ)≥0, 特别地, 当δ(ξ)=0时,ξ是平行向量场.
证明取局部单位正交标架场e1,e2,…,en, 规定指标范围1≤i,j,l≤n, 因为

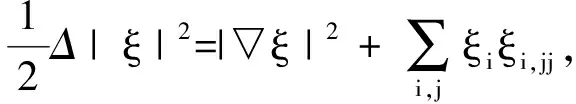
(10)
(11)
将(11)式带入(10)式, 有:
(12)
因为
div(ρξ)=ρdiv(ξ)+<▽ρ,ξ>,
又ρ=div(ξ), 所以上式为:
div(ρξ)=ρ2+<▽ρ,ξ>,
(13)
(14)
从(14)式可以得到ξ的Ricci平均值δ(ξ)≥0, 特别地, 当δ(ξ)=0时,ρ=0且▽ξ=0, 即ξ是平行向量场. 引理1证毕.
引理2设(Mn,g)(n≥2)是黎曼流形, 若Mn上存在非零的平行向量场, 则Mn可以分解成黎曼积Γ×Mn-1, 其中dimΓ=1.
证明设ξ为Mn上非零的平行向量场, 即▽ξ=0, 则对∀X∈X(M)有:
X|ξ|2=X<ξ,ξ>=2<▽Xξ,ξ>=0,
因此
|ξ|2=c2,
其中c为常数.
又因为ξ非零, 所以存在p∈Mn使得ξ(p)≠0, 从而c≠0. 因此|ξ|2≠0(处处). 取局部标架场e1,e2,…,en, 使得

规定指标范围为1≤i,j,k,…≤n, 2≤α,β,γ…≤n. 又ξ=ξiei, 所以有:
ξ1=c,ξα=0,
(15)
由协变导数的定义有:
ξi,jωj=dξi+ξjωji,
则▽ξ=0当且仅当ξi,j=0, 即 dξi+ξjωji=0.
所以有: dξα+ξ1ω1α=0.
(16)
结合(15)式和(16)式有:ω1α=0.
所以Mn有黎曼乘积分解Γ×Mn-1. 引理2证毕.
本文从Δ|ξ|2出发, 然后结合共形向量场的性质并化简后得到共形向量场ξ的Ricci平均值δ(ξ)≥0, 并且δ(ξ)=0时,ξ为平行向量场(引理1). 紧接着, 从平行向量场的定义入手得到了ω1α=0, 即具有非零平行向量场的黎曼流形有黎曼乘积分解Γ×Mn-1(引理2), 结合引理1和引理2即可得到定理2 .
4 结论
本文在Yano和Boncher证明定理的过程启发下, 考虑黎曼流形上光滑向量场的Ricci平均值, 得到了紧定向黎曼流形上一个光滑向量场ξ为共形向量场的必要条件是δ(ξ)≥0, 并且给出了δ(ξ)=0时黎曼流形的分类, 即此时Mn有黎曼乘积分解Γ×Mn-1.

