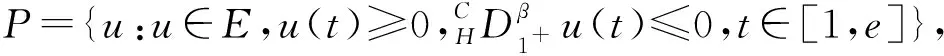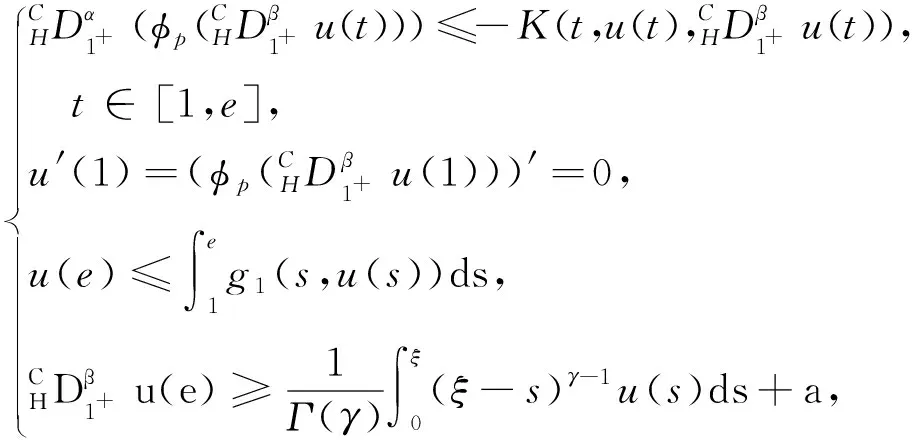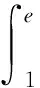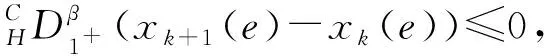一类具有p-Laplacian算子的Caputo-Hadamard型分数阶微分方程解的存在性
南军平, 胡卫敏, 苏有慧, 楚 阳
(1. 伊犁师范大学 数学与统计学院, 新疆 伊宁 835000; 2. 徐州工程学院 数学与统计学院, 江苏 徐州 221116; 3. 伊犁师范大学 应用数学研究所, 新疆 伊宁 835000; 4. 苏州大学 数学科学院, 江苏 苏州 215006)
分数阶微分方程在生物等众多领域得到了广泛的应用,使得分数阶微分方程理论得到了快速的发展,出现了大量关于它的专著和文献,详见文献[1-5].现在分数阶微分方程理论中,大部分是关于Riemann-Liouville型和Caputo型[6-8]分数阶微积分的,对Caputo-Hadamard型[9-13]分数阶导数的研究较少.因此,研究Caputo-Hadamard分数阶微分方程具有积极的意义.
Hadamard分数阶导数是1892年由Hadamard提出的,其意义在于积分的核包含一个任意指数的对数函数.在文献[9]中,利用上下解方法证明了如下非线性Captuo-Hadamard分数阶微分方程解的存在性

文献[11]通过上下解方法和不动点定理证明了如下分数阶边值问题解的存在唯一性
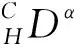
文献[9]研究了非线性Captuo-Hadamard分数阶微分方程,但该方程不带有p-Laplacian算子;文献[11]研究了分数阶微分方程非线性部分不含分数阶导数以及边值条件为整数阶导数,没有研究非线性部分含分数阶导数和边值条件为分数阶导数的情形.受文献[9,11,14-15]启发,本文研究如下一类非线性项包含分数阶导数的具有p-Laplacian算子的分数阶微分边值问题解的存在性
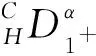
1 相关定义及引理
下面给出一些定义及相关引理.
定义 1[1]令α>0,则函数y:[1,+∞)→R的α阶Hadamard分数阶积分定义为
其中,Γ(·)表示Gamma函数,n-1<α R:δn-1y(t)∈AC[a,T]}. 定义 2[10]1) 如果α≠n,则α>0阶Caputo-Hadamard分数阶导数定义为 HIn-αδny(t). 2) 如果α=n,则n阶Caputo-Hadamard分数阶导数定义为 其中,ci∈R,i=0,1,2,…,n-1. 引理 2若h(t)∈C([1,e],R),c,d∈R,则边值问题 (4) 有唯一解 u(t)=c- (6) 其中 (7) (8) 证明令 边值问题(4)可以分解为以下边值问题: (9) 和 (10) 边值问题(9)由引理1可得 由m′(1)=0可得c1=0.由m(e)=φp(d)有 φp(d), 从而 即 (11) 同理,边值问题(10)可得 由 从而 由Gm(t,s)、Gu(t,s)这2个式子的定义易得下述引理. 引理 3对任意(t,s)∈[1,e]×[1,e],有 Gm(t,s)≥0,Gu(t,s)≥0, 且Gm(t,s)、Gu(t,s)在[1,e]×[1,e]上连续. 记 取范数 ‖u‖=‖u‖1+‖u‖2, 其中 则(E,‖·‖)是Banach空间. 定义 3若u∈AC1[1,e],满足 则称u=u(t)为边值问题(3)的下解. 定义 4若u∈AC1[1,e],满足下述式子 则称u=u(t)为边值问题(3)的上解. 引理 4假设条件: (S1) 若K∈C([1,e]×R×R),对任意t∈[1,e]且0≤n1≤n2,z2≤z1≤0∈R,都有 0≤-K(t,n1,z1)≤-K(t,n2,z2); (S2) 设g∈([1,e]×R),对任意t∈[1,e]且w1≤w2∈R时,有 0≤g1(t,w1)≤g1(t,w2). 若条件(S1)和(S2)均成立,且边值问题(3)存在非负下解xk∈P,k∈{0,1,2,…},则边值问题 存在唯一解 xk+1=xk+1(t)∈P, 且为问题(3)的下解,并满足xk⪯xk+1. 证明由引理2,对任意xk∈P,可知边值问题(14)存在唯一解 xk+1=xk+1(t)∈P, 即 从而有xk+1(t)∈P. 下面证明xk(t)⪯xk+1(t)且xk+1=xk+1(t)是边值问题(3)的下解.由于xk=xk(t)是边值问题(3)的下解,则有 通过(14)和(15)式有 记 则有 则有 可得以下边值条件 通过引理4和(11)式,可得 利用φp的单调性,有 从而可得以下边值条件 因此 xk+1(t)-xk(t)= 即可得xk(t)⪯xk+1(t).由条件(S1)和(S2)可得 即xk+1=xk+1(t)是边值问题(3)的下解. 类似引理4的证明可得下面引理. 引理 5若引理4的条件(S1)和(S2)均成立,边值问题(3)存在上解yk∈P,则边值问题 存在唯一解yk+1=yk+1(t)∈P,且为问题(3)的上解,满足yk+1⪯yk. 定理 1若引理4的条件(S1)和(S2)成立,边值问题(3)存在上解y0和下解x0,且x0⪯y0,其中x0,y0∈P,则边值问题(3)存在解x*和y*,x*,y*∈P,且满足x0⪯x*⪯y*⪯y0. 证明设x0和y0∈P为初始元,由引理4和引理5得到序列{xk}和{yk},并且xk与yk(k=0,1,2,3,…)分别为边值问题(3)的下解和上解.由xk⪯xk+1可知{xk}单调递增;由yk+1⪯yk可知{yk}单调递减. 下面用数学归纳法证明 xn⪯yn,n=0,1,2,3,…. 当n=0时,x0⪯y0成立;当n=k时,假设xk⪯yk成立,即 由引理4的条件(S1)和(S2)有 通过(14)和(17)式有 可得 xk+1⪯yk+1, 即 x0⪯x1⪯…⪯xk⪯…⪯ yk⪯…⪯y1⪯y0, 所以序列{xk}和{yk}一致有界.又由于Gm、Gu和K在[1,e]×[1,e]上连续,且由φp的定义可知φp和φq是连续的,从而序列{xk}和{yk}等度连续.利用Arzela-Ascoli定理可知序列{xk}和{yk}是相对紧的,则存在x*和y*使 下面证明x*和y*为边值问题(3)的解.由Gm、Gu、K和φp的连续性,利用Lebesgue控制收敛定理可得 即 x*=x*(t) 为边值问题(3)的解. 同理 y*=y*(t) 也是边值问题(3)的解,且有 致谢徐州工程学院科研项目(XKY2020102)对本文给予了资助,谨致谢意.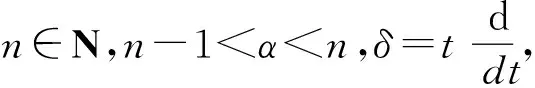
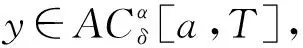
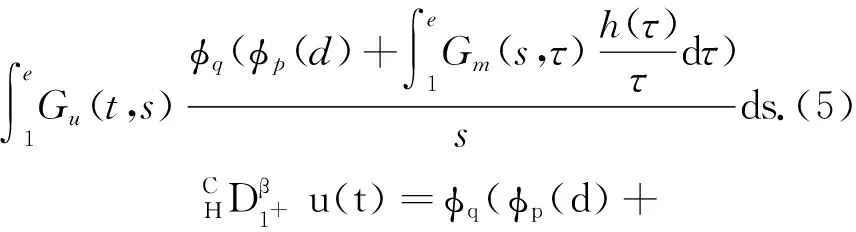
2 解的存在性