基于双量化的双论域多粒度直觉模糊粗糙集

黄心宏, 张贤勇*

(1. 四川师范大学 数学科学学院, 四川 成都 610066; 2. 四川师范大学Laurent数学中心, 四川 成都 610066; 3. 四川师范大学 智能信息与量子信息研究所, 四川 成都 610066)

粗糙集是智能信息处理的基本工具,其相关融合拓展模型具有研究意义,具体实例模型包括文献[1]中融合模糊信息的模糊粗糙集、基于粒度集成的多粒度决策粗糙集[2-3]、文献[4]中基于论域扩张的双论域三支决策粗糙集等.进而,通过“模糊、多粒度、双论域”三要素的不同融合方式,出现了双论域量化模糊粗糙集[5]、双论域多粒度模糊粗糙集[6]、双论域多粒度模糊决策理论粗糙集[7].

直觉模糊信息系统具有粗糙隶属度[8]与非隶属度的双重不确定性刻画优势,相关直觉模糊关系[9]被引入进行粗糙集拓展建模.由此,出现了多粒度支持直觉模糊粗糙集[10]、双论域直觉模糊概率粗糙集[11]以及文献[12]中的双论域多粒度直觉模糊粗糙集等模型.特别地,在直觉模糊信息系统中结合“双论域、多粒度”的粗糙集模型具有理论意义与应用前景,但研究较少;而现有文献[12]使用多粒度直觉模糊集隶属度最值统计来进行集成建模,所得乐观模型与悲观模型具有极端性缺陷.

针对文献[12]中的双论域多粒度直觉模糊环境,本文拟提取双度量均值统计的多粒度融合从而采用双量化集成技术,构建新型粗糙集模型并获取改进性与应用性等.特别地,双量化主要涉及相对度量与绝对度量及其融合,文献[13]提出双近似与双量化交叉双配的2类传统粗糙集,文献[14]进而针对序信息系统建立2类(单粒度)双量化决策粗糙集,而最近的文献[15]则综述了双量化技术及相关研究成果.由此,本文采用文献[13-14]的“双配”双量化策略,对提取的多粒度概率的均值统计[3]以及多粒度基数的均值统计进行集成建模,得到2类扩张改进的均衡性双论域多粒度直觉模糊粗糙集模型,并获得相关优化算法、数学性质、实例分析等.

1 双论域多粒度直觉模糊粗糙集

下面主要回顾直觉模糊关系[9]、文献[12]中的双论域多粒度直觉模糊粗糙集模型.

R={〈(u,v),μR(u,v),νR(u,v)〉|

(u,v)∈U×V}

表示双论域U、V上的直觉模糊关系,其中μR(u,v):U×V→[0,1]与νR(u,v):U×V→[0,1]分别表示对象u、v具有关系R的隶属度和非隶属度.这里(U,V,R)为双论域直觉模糊近似空间.进而,直觉模糊关系的截集为

R(λ1,λ2)(u)={v∈V|μR(u,v)≥λ1,

vR(u,v)≤λ2},

其中,截集参数λ1+λ2∈[0,1].将R粒度扩张成一族直觉模糊关系R1,R2,…,Rm,进一步表示成

Ri={〈(u,v),μRi(u,v),νRi(u,v)〉|

(u,v)∈U×V}∈IF(U×V), i=1,2,…,m.

因此,可构建双论域多粒度直觉模糊近似空间(U,V,Ri).

定义 1[12]在(U,V,Ri)中,Ri∈IF(U×V),集合Y⊆V的下、上近似分别定义为：

(1)

其中

(2)

针对双论域多粒度直觉模糊粗糙集,定义1采用(非)隶属度取最值的方式进行模型构建,相关模型具有传统多粒度建模的乐观与悲观机制[12].由于取最值方式的偏差,所得模型具有极端性缺陷.因此,下面采用双量化策略[13-14]建立改进模型与性质研究.

2 双论域多粒度直觉模糊粗糙集的双量化建模

在双论域多粒度直觉模糊粗糙集环境中,针对定义1((1)和(2)式)复杂的表现形式,本节采用双量化技术[13-14],建立2类新型双论域多粒度直觉模糊粗糙集模型.具体地,基于文献[14]的描述框架,加入条件概率P,采用文献[3]的多粒度概率统计均值方法,进而进行双量化集成建模.双量化近似刻画涉及绝对度量、相对度量比较阈值0<β≤0.5≤α<1,程度k∈N.

定义 2[14]在S=(U,AT,V,f)中,属性集AT={a1,a2,…,an},T⊆AT,f:U→Vaj(j=1,2,…,n).∀X⊆U,基于优势关系的Ⅰ型双量化粗糙集的下、上近似分别定义如下：

(3)

其中

进而,Ⅱ型双量化粗糙集的下、上近似分别定义如下：

T≥={(w,u)∈U×U|

f(w,a)≥f(u,a),∀a∈T}

为优势关系.

(5)

(6)

从层次扩张层面,将文献[11,14]中R的直觉模糊关系截集、条件概率,更新成Ri的直觉模糊关系截集((7)式)、条件概率((8)式).

(Ri)(λ1,λ2)(u)={v∈V|μRi(u,v)≥λ1,vRi(u,v)≤λ2}.

(7)

P(Y|(Ri)(λ1,λ2)(u))=

(8)

定义 3(Ⅰ型均值模型) 在(U,V,Ri,P)中,Ri∈IF(U×V),∀Y⊆V,基于双量化的Ⅰ型均值多粒度直觉模糊粗糙集的下、上近似分别定义如下：

|(Ri)(λ1,λ2)(u)∩Y|)≤k},

当m取1时可得到基于双量化的Ⅰ型单粒度直觉模糊粗糙集.进而,(9)式对应的正域、负域、上边界域、下边界域、边界域及精度定义如下：

命题 1在(U,V,Ri,P)中,Ⅰ型均值模型的基数与所得单粒度模型基数的平均之间无必然相等关系,即

定义 4(Ⅱ型均值模型) 在(U,V,Ri,P)中,Ri∈IF(U×V),∀Y⊆V,基于双量化的Ⅱ型均值多粒度直觉模糊粗糙集的下、上近似分别定义如下：

命题 2(U,V,Ri,P)中,Y⊆V,0<β≤0.5≤α<1,Ⅰ型均值模型与Ⅱ型均值模型的下上近似算子之间关系如下：

针对双论域多粒度直觉模糊粗糙集背景,首先从多粒度层面,更新R的直觉模糊关系截集[11]和条件概率[14].进而,依托定义2的2类(单粒度)双量化模型,建立2类基于双量化的双论域多粒度直觉模糊粗糙集,得到“下近似绝对量化-上近似相对量化”模型和“下近似相对量化-上近似绝对量化”模型,即Ⅰ型均值模型和Ⅱ型均值模型,且以Ⅰ型均值模型为例,给出对应的三支区域及精度((10)式).具体地,采用文献[3]的方式,将绝对度量和相对度量进行均值统计,实现粒度扩张,从而采用双量化集成策略得到2类均值模型.当新建2类均值模型的粒度为1时,可退化得到基于双量化的2类单粒度直觉模糊粗糙集;进一步,若直觉模糊关系退化为优势关系,则可退化成基于优势关系的单粒度双量化粗糙集[15].由于模型构建过程未使用常规的(非)隶属度取最值的方式去定义乐悲观模型,从而简化多粒度直觉模糊集的表现形式.因此,所得模型具有理论扩张性与改进性.此外,基于定义3可得,“量化平均的多粒度集成”与“量化集成的统计平均”之间不具有交换性,因此得到命题1中的Ⅰ型均值模型的基数与所得单粒度模型基数的平均之间无必然相等关系,且对于Ⅱ型均值模型也具有类似结论,由相关定义易证.命题2则进一步探讨2类均值模型下上近似算子之间的关系,结果由相关定义可证.其中,考虑参数k,Ⅰ型均值模型的下近似算子与Ⅱ型均值模型的上近似算子之间包含关系不成立;只考虑参数α、β,Ⅰ型均值模型的上近似算子包含Ⅱ型均值模型的下近似算子.

算法1给出所建立2类均值模型近似算子的计算算法.通过双循环,分别将绝对度量和相对度量进行统计均值,进一步判别元素,从而得到对应的下上近似结果.

算法 1Ⅰ型均值模型与Ⅱ型均值模型的下上近似计算算法:

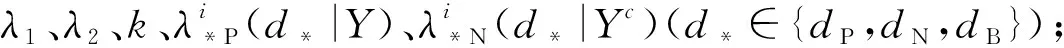
输出:Ⅰ型均值与Ⅱ型均值模型的下、上近似.

1:由(5)和(6)式计算α、β,

2:foru∈Udo,

3:forRi∈{R1,R2,…,Rm} do,

4:计算(Ri)(λ1,λ2)(u)、|(Ri)(λ1,λ2)(u)∩Y|、|(Ri)(λ1,λ2)(u)|-|(Ri)(λ1,λ2)(u)∩Y|、P(Y|(Ri)(λ1,λ2)(u))((7)～(9)和(11)式).

5:end for,

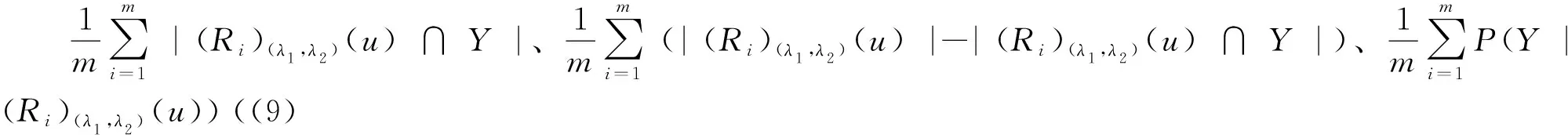
7:由(9)和(11)式的对应条件判别u,

8:end for,

9:得到与返回

3 双量化模型性质

对于所建立的2类均值模型(定义3和定义4),本节研究近似算子的集合运算、阈值单调性等相关性质.主要以Ⅰ型均值模型为代表,Ⅱ型均值模型也具有类似结论.这些多粒度性质主要基于文献[14]单粒度性质的粒度扩张得到,证明方法具有类似性.由于大部分性质具有集成性、传递性、准确性,因此,对于部分性质通常选取一个代表进行证明.

性质 1在(U,V,Ri,P)中,关于全集与空集有：

证明由定义3可证.证毕.

性质 2在(U,V,Ri,P)中,关于下、上近似的包含关系、子集、交并补运算有：

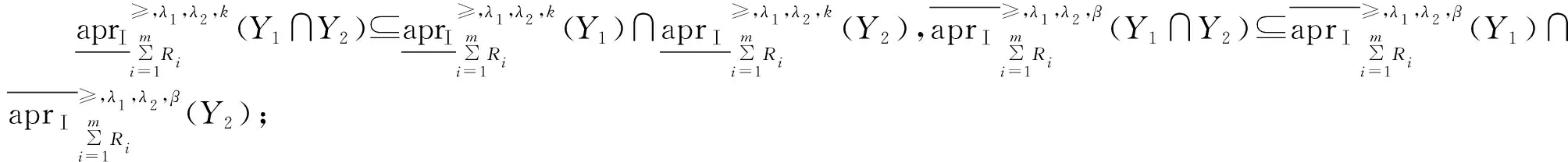
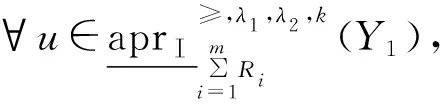
|(Ri)(λ1,λ2)(u)∩Y2|)≤

|(Ri)(λ1,λ2)(u)∩Y1|)≤k,

性质 3在(U,V,Ri,P)中,∀Y⊆V,若k1≤k2,关于参数k的单调性有

证明由定义3易证.证毕.

针对2类均值模型的下上近似算子,性质1～3分别讨论关于下、上近似算子的全集、空集运算,包含关系、子集、交并补集合运算及参数单调性,所得结果关联并深化了文献[14]的对应结果,但部分性质获得了弱化的新结果.具体地,性质1对空集、全集运算进行了粒度扩张;性质2基于文献[14]进一步考虑近似算子补集的运算性质,获得了弱化的新结果,但包含关系、子集、交、并集合运算具有扩张性;由于本文α、β可通过公式计算得到,因此,性质3只考虑参数k的单调性,且扩张后的近似算子对于参数的单调性仍成立.上述这些情况后面将由实例进行验证.

4 实例分析

本节通过企业供应链绩效评价实例,分析说明构建模型及其数学性质.

4.1 模型说明对于企业供应链绩效评价问题,论域U={u1,u2,u3,u4,u5}为企业集合,V={v1,v2,v3,v4,v5}为属性,其中,v1为客户资源,v2为财务环境,v3为技术水平,v4为运营状况,v5为销售能力.4个专家对企业及其属性的评价用直觉模糊关系来表示,见表1.

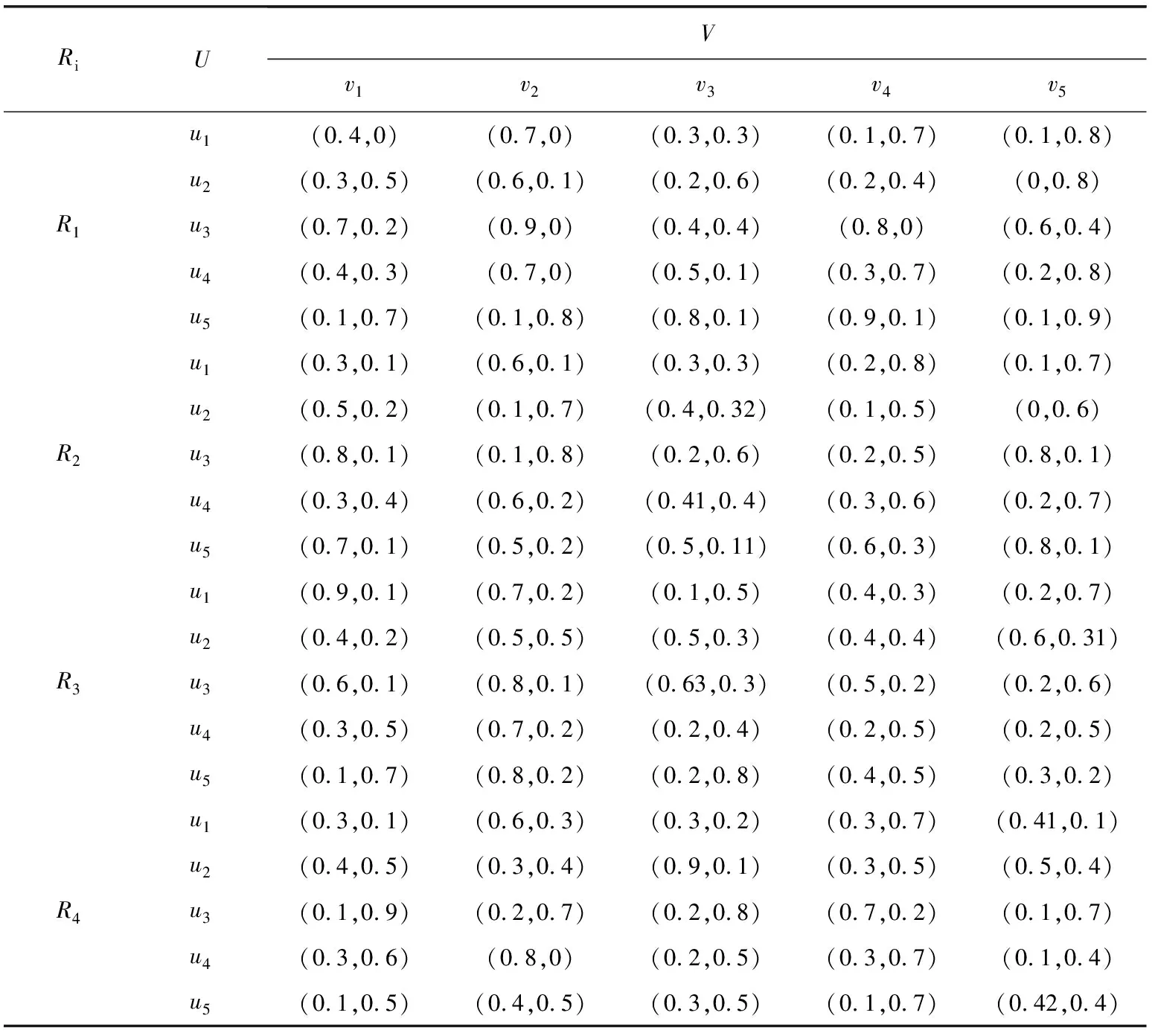
表 1 企业与属性之间的直觉模糊关系

表 2 关系截集、绝对量化和相对量化计算结果

进一步由(9)和(10)式可得出Ⅰ型均值模型的下、上近似、三支区域及精度的结果,也可由算法1得出.

|(Ri)(λ1,λ2)(u)∩Y|)≤k}={u3,u4,u5},

{u1,u2,u3,u5};

{u1,u2,u4};

根据上述Ⅰ型均值模型三支区域结果,实施三支决策方案,得到相关的决策制定方案如下：

1) 企业u3、u5供应链绩效较好;

2) 企业u1、u2、u4需要更多的信息从而进一步判断.

Ⅱ型均值模型及两类单粒度模型也可类似计算.表3给出k的取值为1、2、3、4时,Ⅰ型均值模型与Ⅱ型均值模型的相关结果.根据表3的实例结果,可分析揭示2类均值模型下上近似算子之间的关系、只考虑参数k的单调性,从而验证命题2、性质2的第1)条、性质3.Ⅱ型均值模型的语义及决策可类似解释.对比表3的2类均值模型计算结果可得,k的取值越大,2类模型所对应边界域的基数越小,即不确定的元素就越少,但k的取值与对应精度值并无直接关系.此外,表4给出k取值为2时,2类均值多粒度模型与退化所得单粒度模型的计算结果.由表4实例结果可得出2类均值多粒度模型的基数与退化所得单粒度模型基数的平均之间无必然相等关系,从而验证命题1.2类单粒度模型的语义及决策也可类似解释.另外,值得说明的是,在精度上,通过粒度融合得到的多粒度模型精度值并不高于单粒度模型.

相比文献[12],新建Ⅰ型均值模型采用双量化技术来进行改进建模,定义1模型[12]在本例中的近似算子结果如下：

{〈u1,0.1,0.6〉,〈u2,0.4,0.5〉,〈u3,0.7,0.2〉,

〈u4,0.2,0.6〉,〈u5,0.7,0.1〉},

{〈u1,0.6,0.1〉,〈u2,0.5,0.2〉,〈u3,0.7,0.2〉,

〈u4,0.6,0.2〉,〈u5,0.42,0.4〉}.

通过对比可得,文献[12]模型的模糊集表现形式更加复杂,而新型Ⅰ型均值模型的粗糙集表现形式更简便、直接并具可解释性,有利于决策制定.

对比文献[14],在本例中,与文献[14]的相应结果类似,发现2类模型的三支决策方案并不完全相同.具体地,当k=2时,通过表3所示的2类模型三支区域的结果,使用三支决策制定方案,即Ⅰ型均值模型得出企业u3、u5供应链绩效较好,企业u1、u2、u4需要更多的信息从而进一步判断;Ⅱ型均值模型得出企业u5需要更多的信息从而进一步判断,企业u1、u2、u3、u4供应链绩效不好.因此,在实际决策时,可以同时考虑2类模型,将结果进行比较分析,并根据实际需求得出决策,也可通过进一步定义2类模型对应的风险函数,从而对所得三支区域结果进行比较分析,得出最终决策.

从表4的2类均值多粒度模型与退化所得单粒度模型的计算结果可得,单粒度模型的三支区域结果并不相同,而通过粒度融合,2类均值多粒度模型分别得出最终结果,对于2类均值模型最终结果的不完全一致性,也可根据上述论述得出决策结果.

表 3 Ⅰ型均值模型与Ⅱ型均值模型的实例结果

表 4 2类均值多粒度模型与退化所得单粒度模型的实例计算结果(k=2)

相比退化所得单粒度模型而言,得出构建均值多粒度模型对于信息融合的集成性.

4.2 性质验证下面以Ⅰ型均值模型为代表验证部分性质.数据继续采用上述的λ1=0.3,λ2=0.5,k=2,β=0.287 7,Y={v3,v4}及相应计算结果.

首先说明性质1.

因此,性质1成立.

下面验证性质2的第2)～5)条,Y1={v3,v4}.

2) 取Y2={v1,v3,v4},使Y1⊆Y2有

另取Y2={v1,v2,v4},有

{u3}⊆{u1,u2,u3,u5}=

因此,性质2的第2)～5)条成立.

5 结束语

本文在双论域多粒度直觉模糊环境下,将双度量进行统计均值,进而采用双量化集成策略,建立2类基于双量化的双论域多粒度直觉模糊粗糙集模型,得到相关算法、近似算子性质,其主要以Ⅰ型均值模型为代表.建立的2类均值模型简化文献[12]模型的复杂表现形式,将文献[14]的性质进行理论拓展,具有改进性、扩张性、应用适用性.后续相关的群决策制定、规则提取、属性约简还值得进一步深入研究.