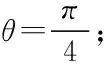对数势条件下双层正方形中心构型的扭转角问题
曾小华, 赵甫荣, 李树勇*
(1. 四川师范大学 数学科学学院, 四川 成都 610066; 2. 绵阳师范学院 数理学院, 四川 绵阳 621000)
1 预备知识
牛顿n体问题[11]研究的是n个质点在万有引力作用下的运动规律,其质量和位置向量分别为mj∈R+,qj∈R3,在牛顿万有引力作用下,质点的运动方程为
(1)
其中,q=(q1,q2,…,qn)∈R3n,牛顿势函数
(2)
定义空间
X={q=(q1,q2,…,qn)∈R3n:
(3)
即质心在原点.
因为2质点碰撞时是奇异的,所以构型空间不应该出现这样的集合,Δ={q:qk=qj对k≠j}.
XΔ叫做构型空间.
定义 1[12-13]一个构型q=(q1,q2,…,qn)∈XΔ被称做中心构型,若存在一个正常数λ,使得下列方程成立
-λmkqk, 1≤k≤n.
(4)
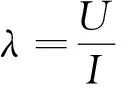
称为α-齐次势函数,当α=1时即为牛顿势函数.
定义 2势函数为如下形式
称为对数势函数,记为U0,即
在R3中考虑这样一个构型,由2层正n边形构成,这2层之间的距离为h≥0,假设下层的正n边形位于水平面,上层的正n边形平行于下层的正n边形,z轴垂直通过这2个正n边形的中心,假设mk(1≤k≤n)是下层正n边形顶点qk处的质量,mn+k是上层正n边形顶点qn+k处的质量,其中
(5)
这里的θ称为扭转角,a>0,h>0为这2层正多边形之间的距离.质心为
(6)
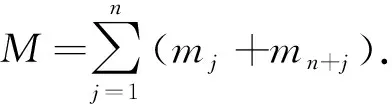
由于按照(5)和(6)式选取坐标系,质心不在坐标原点,为方便计算,作如下坐标平移,令
Pk=qk-z0,k=1,2,…,n,Pn+k=qn+k-z0,k=1,2,…,n.
(7)
在对数势条件下,(q1,q2,…,qn,qn+1,qn+2,…,q2n)构成中心构型,则存在λ*∈R使得下式成立
即
-λ*mk(qk-z0), 1≤k≤2n,
(8)
等价于
-λ*mkPk, 1≤k≤n,
(9)
-λ*mn+kPn+k, 1≤k≤n.
(10)
为得到本文结果,现需引入一个引理.
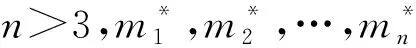
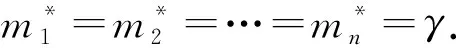
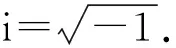
所以
即质心在原点.
当n为奇数时,设n=2l+1,l为整数,则
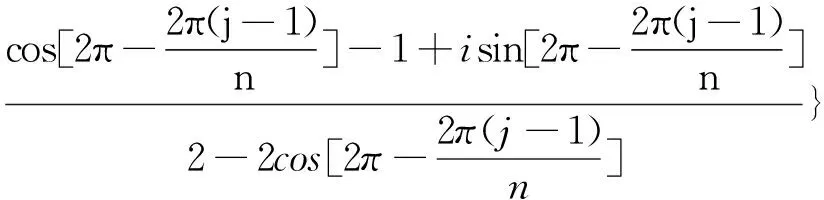
(11)
当n为偶数时,设n=2l,l为整数,则
(12)
(13)
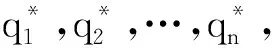
k=1,2,…,n,
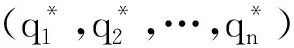
2 主要结果
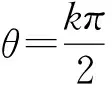
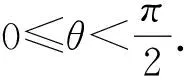
q1=(1,0,0),q2=(0,-1,0),
q3=(-1,0,0),q4=(0,1,0),
q5=(acos θ,asinθ,h),
当θ=0时,这8个天体的位置关系如图1所示.
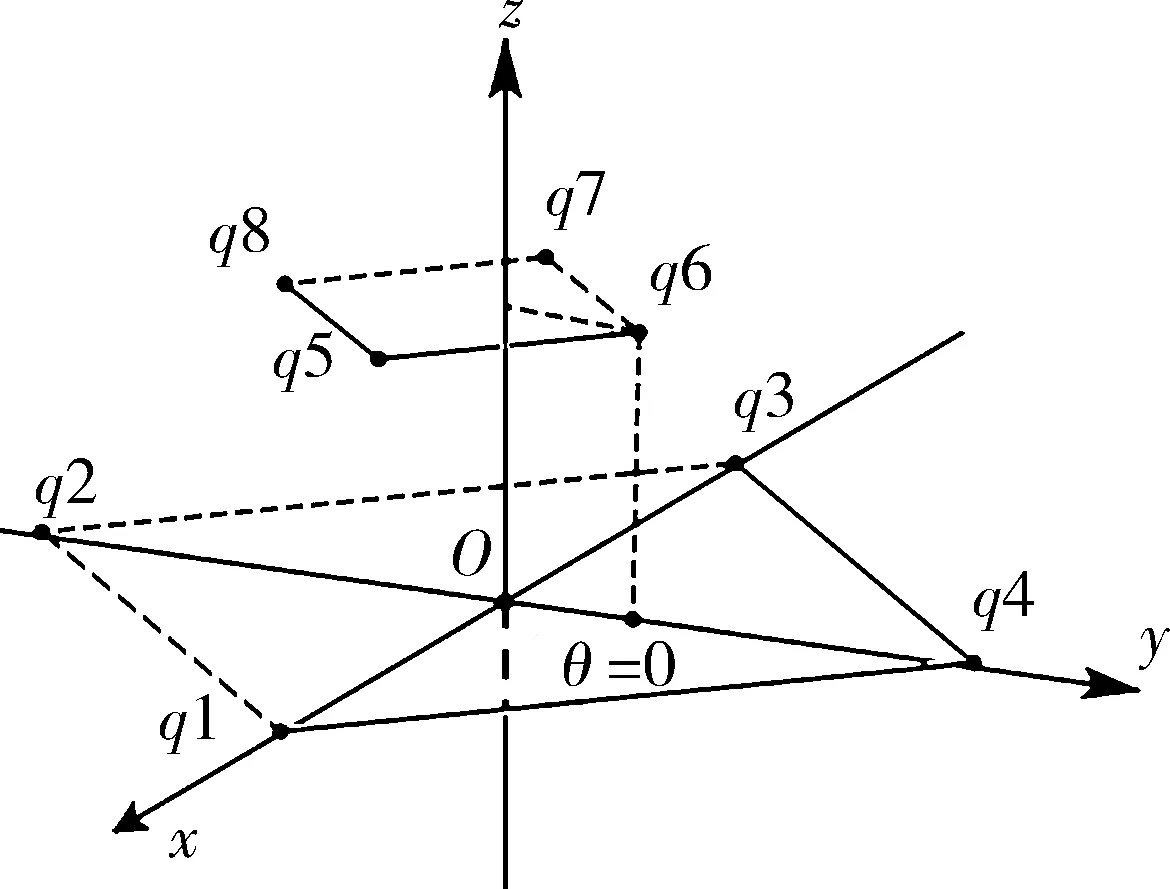
比例尺1∶2
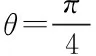
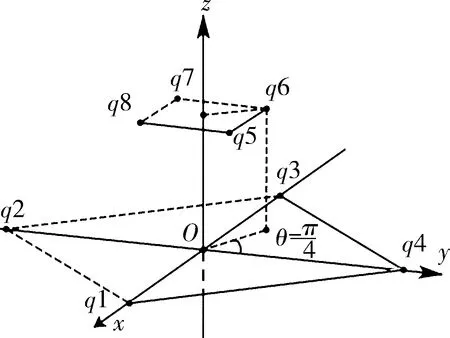
比例尺1∶2
假设m1=m2=m3=m4=1,m5=m6=m7=m8=m,这8个天体的质心为
因为这8个天体构成中心构型,根据中心构型的定义,对于第5个天体q5可得
即
-λ0m5(q5-q0).
(14)
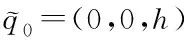
由上式两端的第一个和第二个分量相等可得:
(15)
(16)
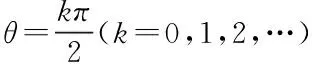
(17)
(18)
由(17)和(18)式可得
(19)
在(19)式的等式左右两边同时除以sin θcosθ,可得
(20)
即
(21)
令
那么(21)式等价于f(cos θ)=f(sinθ).下面将证明当x>0时,f(x)是严格单调递增的.计算下式
令
g(x)=
-(1+a2+h2-4ax)(1+a2+h2+2ax)2+
(1+a2+h2+4ax)(1+a2+h2-2ax)2,
则
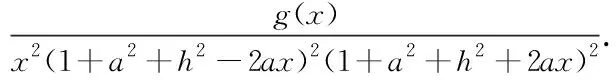
(22)
在x=0处,有
g(0)=-(1+a2+h2)(1+a2+h2)2+
(1+a2+h2)(1+a2+h2)2=0.
(23)
为了判断函数f(x)的单调性情况,需要对g(x)求导,得
4a(1+a2+h2-4ax)(1+a2+h2+2ax)+
4a(1+a2+h2-2ax)2-
4a(1+a2+h2+4ax)(1+a2+h2-2ax)=
4a[2(1+a2+h2)2+8a2x2]-
4a[2(1+a2+h2)2-16a2x2]=
96a3x2>0, ∀x>0.
(24)
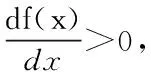
f(sin θ)=f(cosθ),