经历数形结合过程 感悟数形互助内涵——《数与形》教学

文|戚彩红 田小红

【教学内容】

人教版六年级上册第八单元第一课时。

【课前思考】

《数与形》一课的教学，例题和练习中每道题的规律都不一样，很容易上成找规律的课。小学数学中“数形结合”思想散落于各个年级之中。如：数量关系通过“数”来描述数与数之间的关系，画图分析数量关系就是“形”的表现形式；长度、面积、体积是通过“形”来展现其直观形式的，而计算公式又是通过“数”来呈现的；在“统计与概率”中，“数”与“形”更加清晰。受小学生的年龄特征和认知特点所限，思想方法常隐含在众多的数学知识之中。《数与形》一课就是把这层窗户纸捅破，让学生体验“数形结合”的数学思想和方法。《义务教育数学课程标准（2022年版）》中指出，学生几何直观素养的具体表现之一在于能够建立形与数的联系，构建数学问题的直观模型，探索解决问题的思路。所以本课不应停留在让学生会用总结得出的规律解决问题，更重要的是让学生在学习过程中感悟数形结合的思想方法，能用数学的思维解决问题。

为了解不同教材采用的不同图形中哪种更能引发学生思考，笔者进行了前测（见文末二维码）。根据前测结果，我们改变教学素材，采用圆点图，充分发挥学生的自主探究能力。

【教学过程】

一、初步体验数形结合——数中有形，形中有数

动态依次出示下图

师：你看到了什么形状？

生：圆点搭成了三角形。

师：你能计算出这里第六个图形一共有多少小圆片吗？说说你是怎么计算的。

生1：1+2+3+4+5+6=21。

生2：1+2+3+4+5+6=（1+6）×6÷2=21。

生3：1+2+3+4+5+6=（1+6）×3=21。

课件演示生2 和生3 的算理：

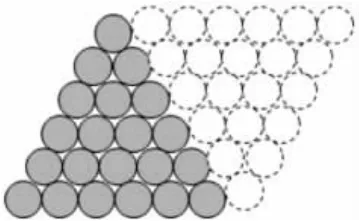
小结：从1 开始的连续自然数相加的和=（1+末项）×项数÷2，并且末项=项数。

师：像1、3、6、10、15……用圆点表示这些数，我们发现这些圆点都可以摆成等边三角形。2500多年前的古希腊，数学家毕达哥拉斯，就发现了这些数的特点，他称这样的数为“三角形数”。你还能继续往下找三角形数吗？你是怎么找到的？

生：三角形数就是从1 开始的连续自然数相加的和。

师：回顾刚才的学习，我们先看到了图形，接着用算式表示了圆点的总数，然后又用图形帮助我们找到了简便计算的方法。有数，也有形；数中有形、形中有数，这节课我们来学习《数与形》。

二、经历过程，感受数形互助——依数思形，依形思数

1.认识正方形数，感受“以形助数”

教师出示课件，动态演示三角形数，隐去偶数层：

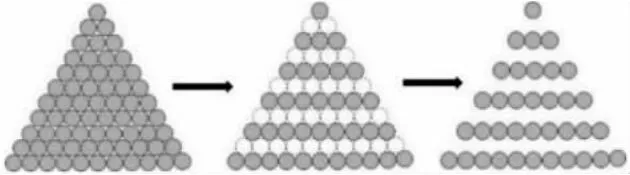
师：你能算出现在这个图形中小圆片的个数吗？说说你是怎么算的。

生：1+3+5+7+9+11=36。

师：能不能像刚才那样用图形来说明计算的过程？请你摆一摆小圆片，看看有什么发现。

师：生2 的方法中你能找到1+3+5+7+9+11 这个算式吗？试着找找看。

师：观察这个图形，有什么发现？

生：摆成了边长是6 的正方形，1+3+5+7+9+11=6×6=36。

生：1+3+5+7+9=5×5=25，摆成了边长是5 的正方形，刚好是5个连续奇数。

师：所以，像1、4、9、16、25、36……这样的数，叫作正方形数。正方形数可以怎样得到呢？

生：正方形数是从1 开始的连续奇数相加的和。

小结：从1 开始的连续奇数相加的和=奇数个数的平方。

2.尝试练习，加深理解

师：想一想，怎样才能算得又对又快？

1+3+5+7+9+11+13+15=__________________=92

1+3+5+7+5+3+1=__________

1+3+5+7+9+11+13+11+9+7+5+3+1=______________

生：想到这个式子的图形，计算就快了。

课件演示：

小结：图形帮助我们解决了计算的问题。

3.探究方阵图，感受“以数解形”

师：（出示6×6 的方阵图）你能用哪些算式来计算这里一共有多少个圆点？想到几种就写几种。

（学生独立操作，交流反馈作品）

师：同学们，回顾一下刚才我们的探究过程。在探究正方形数时，我们从一个算式想到相对应的形，形帮助我们解决了数的计算问题；在探究6×6 方阵图时，用算式来解决这个形的问题，我们发现可以有很多不同的算法，最终结果都是36 个。现在你们觉得数和形之间有着怎样的关系呢？

生：数和形关系密切，你中有我，我中有你，互相帮助。

小结：看到数，我们可以想象它对应的形；看到形，我们可以想它对应的数。数形结合，可以帮助我们解决问题。

三、深刻感悟数形内涵——数形紧密联系、不可分割

1.探究长方形数，解决问题

师：研究了三角形数、正方形数，让我们猜想一下，有没有长方形数？五边形数、六边形数……这样的数呢？来看看刚才的作品，有没有给你启发的地方？

学生思考后，教师课件演示：

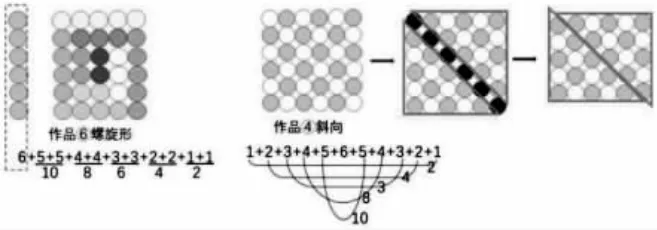
生：作品⑥和作品④去掉6，都可以转化成2+4+6+8+10 这样的从2 开始的连续偶数相加。

生：我发现圆点组成了长和宽分别是5 和6 的长方形。

师：你能在长方形圆点图中找到2+4+6+8+10 这个算式吗？

生：这样图画得更加清晰一些。

小结：（1）从2 开始的连续偶数相加的和是长方形数。（2）从2开始的连续偶数相加的和=偶数的个数×（偶数的个数+1）。

2.梳理关系，深化理解

师：三角形数、正方形数、长方形数之间有没有关系？如果有，是怎样的关系？要寻找它们之间的关系，我们把它们都摆在一起来找找看。

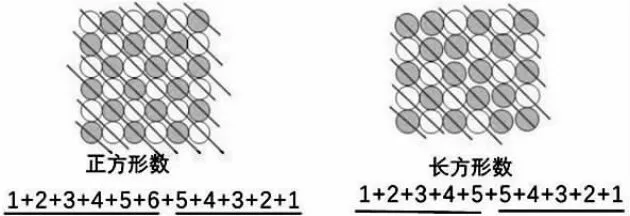
生1：两个相邻的三角形数可以组成一个正方形数。

生2：两个完全一样的三角形数可以组成一个长方形数。

根据学生的回答，出示课件：

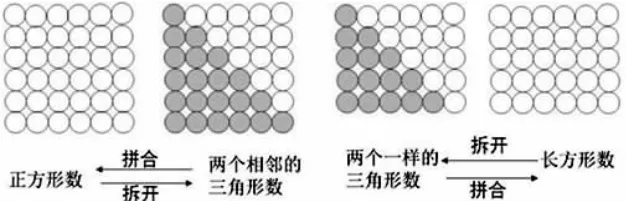
师：毕达哥拉斯学派坚信“万物皆数”，他们还找到了最完美的数、完全数、亲和数、勾股数等。有三角形数、正方形数、长方形数，还有五边形数、六边形数等等，同学们可以在课后继续研究。