着力培养学生的模型意识
——《加法数量关系》教学设计(一)
文|顾 悦
【教学内容】
加法数量关系“总量=分量+分量”,适用于三年级学生。
【教学过程】
一、观察数据,提出问题
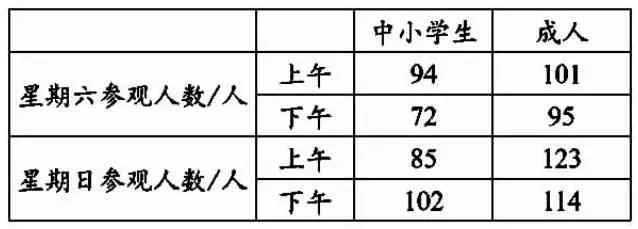
师:同学们,国家天文台最近有一个新展览,吸引了不少人前来打卡参观。工作人员统计了星期六和星期日接待的参观人数,让我们一起来看看。(出示下表)
?
师:这个表格你能看懂吗?考考你们,这里的72 表示什么意思?
生:表示星期六下午参观的中小学生人数。
师:看来这一个数的意义不仅要横着看一看,还要竖着看一看。接下来比比大家的眼力,能不能在表格中快速找到需要的数据,星期日上午参观的成人人数是多少?
生:123。
师:相信同学们对于表格中的数据都非常清楚了,那你能根据表格中的数据,提出一个用加法计算的问题吗?
生:星期六一共有多少人参观?星期六上午一共有多少人参观?星期日一共有多少成人参观?……
师:同学们的发言真踊跃,想到了这么多的问题。
(依次出示三个问题)
1.星期六上午一共有多少人参观?
2.星期六一共有多少中小学生参观?
3.星期六一共有多少人参观?
【设计意图:创设真实且信息含量丰富的情境,让学生解读表格、理解数据含义,提出用加法计算解决的问题。如此,有助于学生形成具有思维含量的真问题,形成具有关联性的问题链,也培养了学生独立发现问题、提出问题的能力。】
二、归纳概括,发现关系
1.自主表征,初步发现数量关系
师:让我们先来看第一个问题“星期六上午一共有多少人参观”,你会解决吗?
出示活动要求:(1)先列出算式算一算;(2)为什么用加法计算?把你的思考画一画、写一写。
(学生小组活动,教师巡视之后交流学生作品)
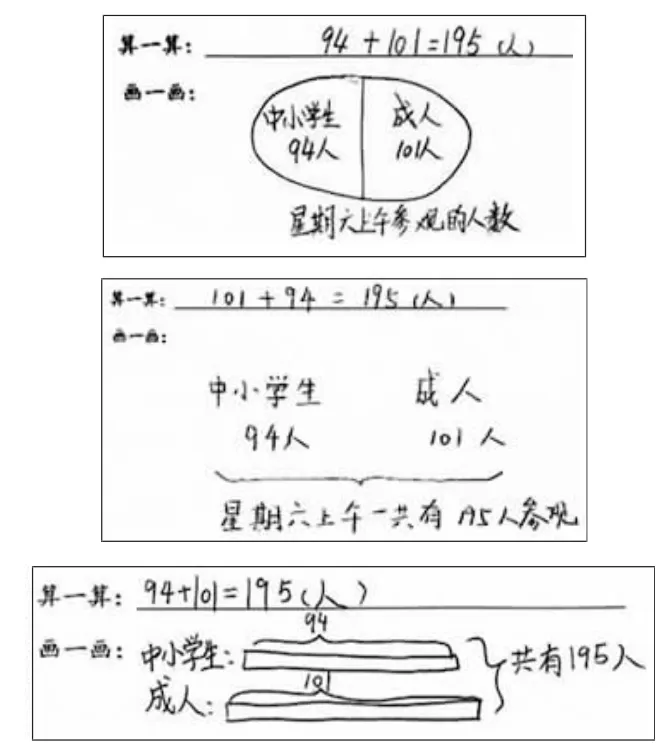
师:这三幅作品画法不同,都能解释为什么用加法计算,那它们有什么相同的地方呢?
生:这几幅作品都表示把两个部分合起来。
师:是的,不管是圈、括,还是连,都可以表示把两部分合起来。那是把哪两个部分合起来呢?
生:都表示把星期六上午参观的中小学生人数和星期六上午参观的成人人数合起来。
师:这两个部分合起来就是?
生:星期六上午参观的人数。
师:真好!星期六上午参观的人数=星期六上午参观的中小学生人数+星期六上午参观的成人人数,这就是这个加法问题对应的数量关系。
【设计意图:鼓励学生借助已有的学习经验,依托他们对于加法的“原初概念”,用画一画、写一写的方式把加法计算的道理自主表达出来,这种“画数学”的方式,把复杂的数量关系变得简明、形象,在多元表征中异中求同,帮助学生逐步厘清星期六上午参观的人数是由星期六上午参观的中小学生人数和星期六上午参观的成人人数两部分合起来,进而在圈、括、连等形象的方式中蕴蓄加法的数量关系。】
2.丰富素材,进一步发现数量关系
师:刚才提出的“星期六一共有多少中小学生参观”大家也同意用加法计算,解决这个问题,它的数量关系又是什么?
生:星期六参观的中小学生人数=星期六上午参观的中小学生人数+星期六下午参观的中小学人数。
师:再来看看第三个问题“星期六一共有多少人参观?”谁能仿照老师黑板上的关系来说一说星期六一共参观的人数就等于什么?和你的同桌互相说一说。
生:星期六参观的人数=星期六上午参观的人数+星期六下午参观的人数。
师:你能在图中圈一圈吗?
出示:
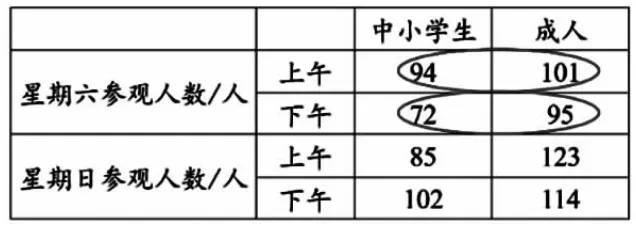
?
(揭示:星期六参观的人数=星期六上午参观的人数+星期六下午参观的人数)
生:我还有不一样的想法。
出示:
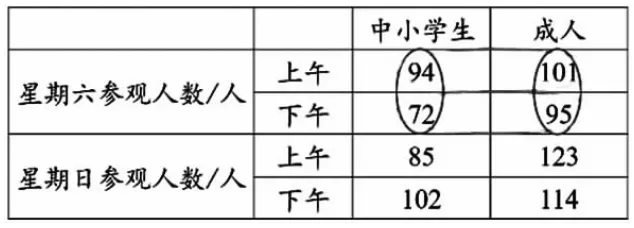
?
(揭示:星期六参观的人数=星期六参观的中小学生人数+星期六参观的成人人数)
师:刚刚两位同学从不同的角度来分析数量关系,都能解决问题。同样是求星期六参观的人数,为什么这两位同学找到了不一样的数量关系?
生:那是因为我们分类的标准不一样,对应的数量关系就不同。
【设计意图:在探究前两个问题的数量关系时,一个问题对应唯一的一个数量关系,而到了第三个问题“星期六一共有多少人参观”时,学生通过多元思考会发现两个不一样的数量关系,进而明白:解决的加法问题相同,对应的总量虽然是一样的,但思考问题的过程中分类标准不同,同样的总量可能会对应不同的分量。】
3.总结提炼,建构加法模型
师:回过头来看刚刚这几个关系式,它们有什么共同特征呢?
生:都表示把两个部分合起来,求的是一共的人数。
师:在数学上也就是总量,加号左边就是总量的一部分,加号的右边也是一部分,我们把它们叫作分量。
(揭示:总量=分量+分量)
师:黑板上三个实际问题中的总量与分量分别是什么?
师:看来这里的三个数量关系都可以用“总量=分量+分量”的数量关系来表示。其实,在数学上还有一个很形象的图示也可以表示加法数量关系,在今天同学们的作品中就有它的影子。
出示:
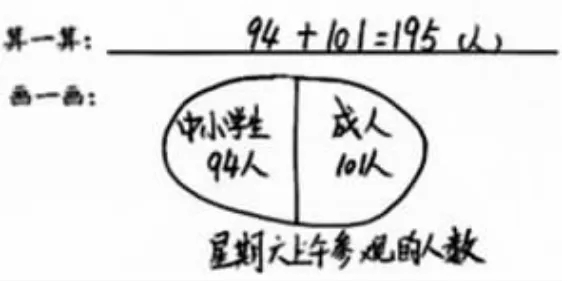
师:如果这个圈表示总量,它的分量在哪儿?伸出小手指一指。
师:数学上是怎样表示的呢?我们一起来看。
出示:

4.理性思辨,理解“此分量对应彼总量”
师:我们解决第一个问题的时候,星期六上午的人数是总量,到了第三个问题,为什么它却变成了分量?
生:因为在第一个问题里,要求星期六上午的人数,在这个问题里它就是总量;而在第三个问题里,要求星期六一共参观的人数,这时候星期六上午的人数就是分量了。
生:虽然是同样一个量,看它是总量还是分量,要具体问题具体分析。
师:想一想,星期六一共参观的人数还有可能变成谁的分量?
生:星期六和星期天一共来参观的人数。
【设计意图:数学教育家弗赖登塔尔认为,数学学习的过程是一种“再创造”的过程。学生经历从生活情境中概括数量关系,在对比分析中探寻加法数量关系的本质,从用数学语言表达数量关系,到自我建构了“总量=分量+分量”的加法模型,并逐步过渡到感受数量关系的一致性。同时,让学生感受“总量”“分量”并不是固定不变的,理解“此分量是彼总量”,引导学生具体问题具体分析,形成理性思考的品质。】
三、运用关系,提升认识
1.自主编题
师:生活中,你觉得还有哪些问题也能用到我们今天学习的数量关系来解决?这些问题中,数量关系式是什么?总量是什么?分量是什么?
生1:我们班有女生22 人,男生24 人,我们班一共有多少人?
生2:女生的人数+男生的人数=三(1)班一共的人数。
生3:总量是三(1)班一共的人数。分量是这个班女生的人数和男生的人数。
师:谁还想举例?
生4:家里原来有5 个苹果,妈妈又买回来4 个苹果,家里现在一共有多少个苹果?
生5:总量是家里现在的苹果,分量是家里原来有5 个苹果和妈妈又买回来的4 个苹果。
生6:家里现在的苹果个数=家里原来的苹果个数+妈妈又买回来的苹果个数。
2.拓展应用
师:老师这里还有几道题,这些题都能用加法数量关系来解决吗?如果能,那总量是什么?对应的分量又是什么?
出示:

(1)探究“还原型”的加法数量关系
师:我们先来看题①。
生:原来有的本数=卖出的本数+还剩的本数。
师:题目中说的是卖出和还剩,怎么还有加法数量关系呢?
生:这里原来有的本数是总量,卖出的和还剩的都是分量。
师:看来解决问题,我们不能只看字面的意思,还要关注背后的关系。
(2)理解“比较型”的加法数量关系
师:我们来看题②。
生:吴军折的只数=王芳折的只数+吴军比王芳多的只数。
师:这个问题求的是什么量?
生:总量。
师:那它所对应的分量呢?
生:王芳折的只数是分量,多12 只是另一个分量。
师:真的是这样吗?如果大家觉得有困难,老师给大家请来了线段图帮忙。再仔细观察观察,这里的总量对应的分量是什么?
出示:
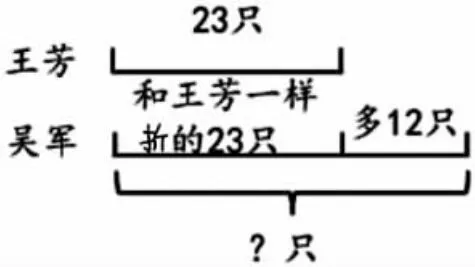
生:分量应该是吴军和王芳一样折的23 只和他比王芳多的12 只。
师:你的感觉真好,这两个分量合起来就是总量,看来有时候分量还藏在题目给定的已知条件中。
(3)减法问题中的数量关系
师:我们来看题③。
生:又放进去鱼的数量=现在水池里鱼的数量-原来水池里鱼的数量。
生:现在水池里的鱼数是总量,原来水池里的鱼数是分量,又放进去一些是另一个分量。
师:你能总结出减法的数量关系吗?
生:分量=总量-分量。
师:真好!把加法数量关系变一变,就能得到减法数量关系式。
(4)感受总量里可以有多个分量
师:最后,我们来看题④。
生:食堂一共采购荤菜的千克数=鱼的千克数+肉的千克数+鸡蛋的千克数。
师:看来这里的总量有3 个分量对应,如果有4 个荤菜、5 个荤菜呢?
生:那就在后面继续加。
师:可是数学上却只用“总量=分量+分量”来概括所有分量相加的情况,这是什么原因呢?
生:不管多少个分量,都是把分量相加,用“总量=分量+分量”来表示就行了。
生:总量可以由两个较大的分量组成,这两个较大的分量还可以继续往下分成更小的分量。
【设计意图:提供全方位素材,拓展加法外延,使学生接触加法实际问题除了常见的合并型、添加型,还有还原型和比较型等类型,深刻感受加法模型可以解决生活中很多的加法问题,具有一定的普适性。因为比较型对学生有一定的挑战性,借助线段图的直观,帮助学生更好地理解总量对应的分量;让学生理解减法是加法的逆运算,利用加法模型,不仅能解决加法问题,还能解决减法问题。】
四、全课总结,分享收获
师:通过今天的学习,同学们一定不仅收获了知识,还学会了方法。带着你收获的知识和方法,去研究更多的数学问题吧。

