提供多维支架 促进深度理解
——《加法数量关系》教学设计(二)
文|江晓丽
【教学内容】
加法数量关系“总量=分量+分量”,适用于三年级学生。
【教学过程】
一、丰富素材,拓宽研究视野
师:课后服务“15 分钟教育圈”让我们的社团学习从校内走向了校外,上周学校就组织美术社团的同学去美术馆观看了主题为“花卉静物三百年”的展览。观展体验非常好,同时他们还发现了这样几个数学问题。

学校美术社团赴美术馆观展人数统计表
问题1:版画社团一共有多少人去观看展览?
问题2:为支持青年艺术家的创作,美术馆专门开辟了一个青年艺术家的作品售卖区,本期艺术家作品已经卖出32 幅,还剩16幅,请问原来有多少幅作品?
问题3:展览后,学校邀请了一位青年艺术家到校开设“创意绘画”专题讲座,同学们报名的热情高涨。三(1)班原有33 人报名参加,后来又增加了6 人参加,三(1)班现在有多少人参加?
师:你能列式计算,解决这三个问题吗?
生:16+23=39(人)。
生:32+16=48(人)。
生:33+6=39(人)。
【设计意图:“15 分钟教育圈”是南京市玄武区教育局基于南京丰富的场馆资源提出的课后服务的创新之举,问题情境是学生生活的真实事件,学生在解决问题的过程中不仅感受到场馆学习对于艺术素养的熏陶和启迪,而且能感受到整个社会对艺术发展的关照和支持,以及艺术是全人类共同语言的美好情感。这样的问题情境容易引发学生解决问题的亲近感,唤醒学生关于加法的已有经验。从数学角度来说,本题的三个情境依次呈现,分别对应着“合并型”“还原型”和“添加型”,拓宽了加法模型的外延。引发学生自然地思考:问题不同,为什么都可以用加法来解决呢?背后会不会有什么相同的地方呢?事件真实、数据合理、素材多元的问题情境有效支持了学生愉悦且不失挑战地探寻数学与思维之美。】
二、搭建支架,引导学生自主建构
1.解决问题,抽象数量关系式
师:三个问题各不相同,为什么都能用加法解决呢?我们以第一个问题为例,说说你的想法。
生:因为要求版画社团的人数,就是要把社团里男生的人数和女生的人数合起来。
师:是的,版画社团的人数=男生的人数+女生的人数(板书呈现此数量关系),这就是第一个加法问题的数量关系。
师:问题2、3 你也能像这样说一说它们的数量关系吗?
(先同桌互说,再交流汇报)
生:原来的作品数量=已经卖出的数量+还剩的数量。
生:现在三(1)班参加的人数=原来参加的人数+后来增加的人数。
2.回归生活,提取丰富的素材
师:生活中这样的问题还有很多,你能编一道用加法解决的问题,并说说它的数量关系吗?跟你的同桌先交流一下。
(学生自主列举一些生活中的加法问题)
师:生活中这些加法问题都能说出像刚刚那样的加法数量关系吗?
生:能。
师:这些加法数量关系说得完吗?
生:说不完。
(板书添加:……)
3.尝试归纳,自主表征关系
师:这么多数量关系看上去各不相同,可都能用加法解决,它们有没有共同特点?你能不能用一个式子或一幅图,把这么多的加法数量关系的共同特点表示出来?
(学生拿出《研究单》,写一写或画一画。教师巡视,收集并展示三幅典型作品)
师:这三幅作品,都能把数量关系的共同特点表示出来吗?
要求:选择一幅作品,具体说说是怎么表示数量关系的共同特点的。
(学生先独立思考,再在组内交流,然后全班交流)
生:图1 是说这几道题都表示把两个部分合起来得到一共的数量。

图1
生:图2 就是把等式换成圆圈和连线来表示了,图3 就是把图1 的文字换成了图形,其实三幅图表示的意思都一样。
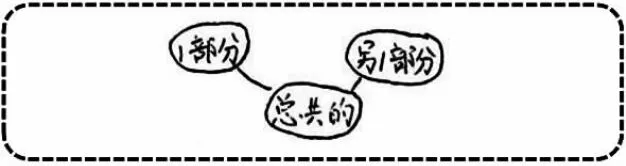
图2

图3
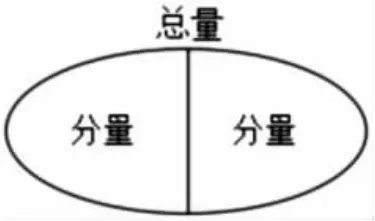
图4
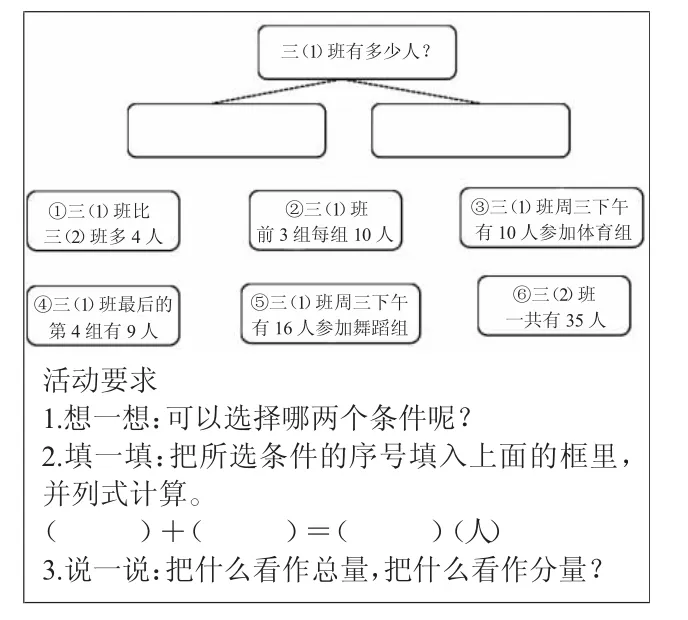
图5

图6
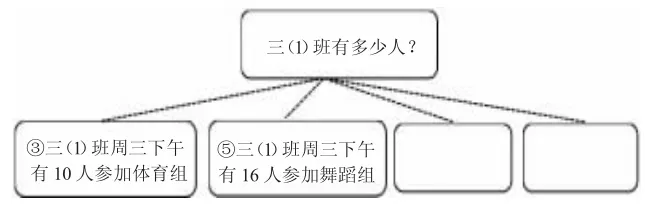
图7
4.提取要素,建构加法模型
师:真会比较,是的,这三幅图有的是用文字来表示,有的是用图形来表示,但是意思确实一样。我们先来看第一个式子,这里的“一共的个数”我们可以叫作“总量”,这“一部分”就是“总量”里的“分量”,“另一部分”也是“分量”。那这三者有什么关系呢?
生:总量=分量+分量。(板书)
师:后两幅作品里能看到总量、分量和分量吗?与同桌说一说。
师:在图3 里,如果去掉后面两个图,就在等号左边这一个图里,还能看到总量和分量吗?
生:能,整个圆形就是总量,左边是分量,右边也是分量。
师:真有洞察力。瞧,数学上就是用这样一幅图来表示的,你们的理解很棒!(出示加法模型的集合图)
师:刚刚我们在解决问题的过程中发现了这些数量关系,找到了它们的共同特点,还用这样一幅简洁的图来表示。这就是我们今天研究的加法数量关系。(揭示课题:加法数量关系)
【设计意图:“三个问题各不相同,为什么都能用加法解决呢?”本环节的第一次追问,引导学生结合每一个问题说出具体的数量关系式。三个例子唤醒了学生对于生活中加法数量关系的经验,通过引导学生举例,为接下来的观察比较、分析概括、梳理共性积累了更丰富的素材。随即,教师进行第二次追问“这么多数量关系看上去各不相同,可都能用加法解决,它们有没有共同特点?”并通过《研究单》提供“写一个式子”或“画一幅图”这样的思维表达的支架,支持学生尝试自主表征,完成儿童化的抽象。最终学生在全班交流讨论中,共同完成加法模型的抽象,并且惊喜地发现自己的理解与数学家的表达是如此高度的相似。本环节,通过两次追问搭建了学生“异中求同”的思维支架,通过“写一个式子”和“画一幅图”有效支持了学生关于加法数量关系的自主建构,收获了与数学家“一致理解与表达”的成就感。】
三、开放练习,在运用中深度理解
1.深入理解“总量”与“分量”的关系
(1)理解“分类标准不同,分量不同”
师:让我们带着对加法的新认识继续来解决问题,回到第一个问题,根据表格中的信息,你能提出一个更复杂的加法问题吗?
生:美术社团一共有多少人参观?
师:你会用今天我们研究的加法数量关系来解决这个问题吗?
生:美术社团的人数=线描写生社团的人数+版画社团的人数。
生:美术社团的人数=男生的人数+女生的人数。
师:同一个总量,为什么会有不同的分量?
生:因为一种是按照社团种类来分的,一种是按照男女生来分类的。
生:因为分类的标准不同,所以同一个总量会产生不同的分量。
(2)理解“不同情境中,此分量可能是彼总量”
师:版画社团的人数在这里是分量,在上一个问题中却是总量,这是为什么呢?
生:因为两题的问题不同呀,在这道题里,总量是美术社团的人数,所以版画社团的人数是它的分量。
师:是的,同一个量,什么时候是分量,什么时候是总量,需要具体问题具体分析。
(3)理解“分量=总量-分量”
师:已知两个分量,求总量我们用加法,那如果已知总量和其中一个分量,求另一个分量,该怎么办呢?
生:求其中一个分量,可以用总量减去已知的一个分量。
2.感受模型的普适价值
师:三(1)班有多少人?你能从老师带来的信息中选择两个合适的条件并解决这个问题吗?请仔细阅读活动要求。
(1)理解“比较型”中的数量关系
师:谁愿意和大家说一说你是怎么选的?
生:我选的是①号和⑥号。
师:选择“三(1)班比三(2)班多4 人”和“三(2)班一共有35人”两个条件,能解决问题吗?请列式解决,想一想这里把什么看作总量,谁是它的两个分量?
生:三(1)班人数是总量,三(2)班人数是一个分量,三(1)班比三(2)班多出来的4 人是另一个分量。
生:我觉得不对,三(2)班的人数怎么会是三(1)班人数的分量呢?
生:你们看这个线段图,我觉得第一个分量应该是三(1)班与三(2)班相等的人数。
师:借助线段图,理清了关系,找到了准确的说法,为你们点赞!
(2)借助乘加问题,深入理解加法模型
生:我选②号和④号。
师:选择“三(1)班前3 组每组有10 人”和“三(1)班最后的第4 组有9 人”可以吗?这个时候,分量是谁呢?
生:“三(1)班前3 组共30人”是一个分量,“三(1)班最后的第4 组有9 人”是另一个分量。
师:看来,把“三(1)班前3 组每组有10 人”当作一个整体,它就是一个分量。
(3)感受总量里可以有多个分量
师:还有不同的选法吗?
师:“三(1)班周三下午有16人参加舞蹈组”和“三(1)班周三下午有10 人参加体育组”这两个信息为什么不选呢?
生:因为它们加起来才26 个人,人数不够啊。
生:应该还漏了别的信息,三(1)班周三下午应该还有人去参加了别的社团,比如足球队、合唱团等等。
师:那样的话,你觉得会有几个分量呢?
生:可能是3 个、4 个,或者很多个。
师:很有道理,可是今天学习的加法数量关系式:总量=分量+分量,为什么只有两个分量呢?
生:这是一种简洁的概括,总量里的分量可以有若干个,但是写出2 个我们就明白意思啦。那要不然写多少个合适呢?
生:像上一题的“三(1)班前3组每组有10 人”,其实就是把3个小分量合并成了一个大一点的分量,所以有些分量是可以合并的,关系式写2 个分量就可以啦。
师:道理说得很清楚,真棒!
【设计意图:本环节设计了一个开放的问题情境,在“挑选合适条件”的思辨中,逐步理解“总量”与“分量”关系的特点,比如“因为分类标准不同,同一个总量,可以由不同的分量组合而成。”“不同情境中,此分量可能是彼总量”,在解决问题的过程中,自主推理出“分量=总量-分量”。同时进一步深化对加法模型内涵和外延的理解,比如在练习中借助“线段图”这一思维支架,有效突破“比较型”中的两个分量如何准确表达这个学习难点。理解“乘加混合的数量关系”也包含在“总量=分量+分量”这个加法数量关系里,理解一个总量可以由多个分量“不重不漏”组成。开放情境,开放了思维空间,让不同水平的学生都可以给出自己的理解,也让学生的认识水平得以在对话交流中实现跃迁,实现了“在运用中深入理解”这一巩固练习环节的初衷。】
四、回顾历程,梳理认识方法
师:一起回顾今天的学习历程。我们先解决了生活中的真实问题,发现了不同的问题都可以用加法来解决;接着通过观察比较、自主创造、全班交流,发现了不同问题背后相同的加法数量关系;最后在运用中又进一步加深了对加法数量关系的理解。我们在学习很多内容时,都会经历这样的过程。
【设计意图:借助课件,引导学生通过回顾学习历程,感受认识新事物的一般路径,积累学习经验,提升数学素养。】

