基于小波Galerkin法的矩形薄板二次屈曲分析*

张 磊，张文明，王 林，李世斌

（1.国防科技大学 空天科学学院，长沙 410073；2.湖北三江航天集团 红阳机电有限公司，湖北 孝感 432000）

引言

自20世纪90年代小波分析理论建立以来，小波数值方法因其在非线性和多尺度计算方面的应用潜力，得到了持续不断的关注和研究，尤其是在非线性力学问题求解方面的应用[1]，例如结构大挠度分析[2]、智能结构振动控制、应力集中和裂纹扩展等应力奇异性问题[3].为了继续发掘小波方法在非线性力学问题求解方面的计算优势，本文在矩形薄板大挠度问题小波解[2]的基础之上，继续采用小波方法对矩形薄板非线性稳定性问题求解与分析.

对于结构完善的弹性平板，当面内压缩载荷超过Euler 屈曲临界值，它们就由平直的初始状态进入横向变形的后屈曲状态，并以屈曲波形的形式保持稳定[4].随着载荷的增加，屈曲波形保持不变而其幅值呈非线性增大.大量理论研究和稳定性实验还表明，矩形薄板在后屈曲变形增大的过程中，还可能存在另一个临界状态，初次的屈曲模态将由稳定变为不稳定，并伴随着屈曲波形的跳跃现象[5]，这个临界状态被称为二次屈曲.上述受压结构也可能不发生二次屈曲，初始屈曲后直接进入塑性屈服而迅速发生破坏.对于二次屈曲之前的后屈曲阶段，只要给定合适的初始值或摄动参数，就可以跨越Euler 屈曲临界值而直接利用Newton 迭代法或者摄动法进行后屈曲分析[6-7].这类方法对于屈曲波形保持不变的初始后屈曲行为是有效的.然而对于二次屈曲和弹塑性屈曲等大范围屈曲行为，则需借助扩展方程法和延拓法等非线性屈曲分析方法实现不同平衡状态的连续追踪和稳定性判断[8-9].结构非线性屈曲分析方法中的空间离散一般使用经典的三角级数[10-11]或非线性有限元格式[12]，其中除Navier 解和Levy 解之外，三角级数在大范围后屈曲阶段的截断误差难以保证.而基于大型有限元程序，为了仅利用切线刚度矩阵而避免其导数计算带来的单元改进和内存增加问题，又发展了基于解流形和切向量旋转度等几何近似方法来计算奇异的分岔点和分岔方向[12].

本文通过结合小波Galerkin 法和不同的非线性屈曲分析方法来求解矩形薄板二次屈曲问题.首先，给出了屈曲问题控制方程的小波离散格式；然后，提出了基于一个扰动方程的切线刚度矩阵计算方法，并讨论了基于小波离散方程求解二次屈曲临界载荷的特征方程和扩展方程，以及进行后屈曲追踪的伪弧长格式；最后，较为详细地讨论了矩形薄板完整的二次屈曲平衡路径和波形跳跃行为.

1 薄板屈曲方程的离散格式

1.1 矩形薄板的屈曲方程

设边长为a和b，厚度为h的各向同性弹性矩形薄板，两对边上分别承受面内压缩载荷px和py以及面内剪切载荷τxy，矩形薄板屈曲问题的控制方程如下[4]：

其中w(x,y)和f(x,y)为中面横向位移和应力函数，D和E为矩形薄板的抗弯刚度和弹性模量，∇4为双调和算子，算子H(w,f)的表达式为

面内可移的四边简支可等效地表示为[2]

面内可移的四边固支可等效地表示为[2]

1.2 小波Galerkin法的离散格式

本文采用基于Coiflet 小波的Galerkin 法，其中修正Coiflet 基函数作为Galerkin法的权函数与试函数.对于定义在有限区间上的函数f(x,y)∈L2[0,1]2，有逼近公式如下：

其中二维平方可积函数空间的基函数由一维空间基函数的张量积生成，一维基函数的表达式[2,13]具体见文后附录.为了适用于四阶板壳方程，选择小波函数消失矩数目为6 和尺度函数一阶矩为7 的Coiflet 小波修正基函数.

为了便于处理控制方程中耦合导数项，首先忽略无量纲化变量的上标，且定义下列新函数：

那么方程（5）可写为

式中Φm,i(x)表示满足边界条件的基函数，代入新函数的表达式且应用Galerkin 法，可得

其中系数矩阵和未知向量分别为

代入方程(8)，且应用Galerkin 法可得

2 二次屈曲分析的小波方法

2.1 Jacobi 矩阵的计算

Von Kármán 方程是个单向耦合问题，利用逆算子建立应力函数f和挠度函数w的映射关系，并代入到离散代数方程组（11）中，可化为如下非线性方程的一般形式：

其中g表示非线性算子.由向量值函数的广义Taylor 定理，可在状态W0附近对上式进行展开：

其中DwG(W0)和DwwG(W0)即为W0处的Jacobi 矩阵和Hesse 矩阵.

引入另一个应力函数fp，且令面内载荷表示为

那么无量纲化方程(5)可表示为

再将平衡路径上某个平衡状态记为(w0,f0)，且假设该状态的扰动量为(wh,fh)，那么控制方程（15）平衡解的扰动形式则为[11]

将式（16）代入方程(15)，展开上式且考虑状态(w0,f0)处的平衡关系，则有

化简后可得原方程的一阶扰动方程

和二阶扰动方程

离散一阶扰动方程（18），可得

由式(20)中第二式可得展开式（13）中的一阶扰动项，即方程（12）的Jacobi 矩阵：

离散二阶扰动方程(19)，可得

由式(22)中第二式可得展开式（13）中的二阶扰动项，即方程（12）的Hesse 矩阵：

2.2 二次屈曲分析的方法

由隐函数定理可知，当Jacobi 矩阵DwG(W0,λx,λy,λxy)非奇异时，方程存在唯一解.而依据屈曲问题的多解性质可知其Jacobi 矩阵奇异，即有

方程（24）为非线性特征方程，一般为超越方程，直接求解非常困难.考虑仅有λx的单向屈曲问题，假设后屈曲平衡状态w0为基本状态，可得到由位移增量表示的线性特征方程：

因此二次屈曲的临界条件也可表述为后屈曲路径上某处载荷值恰好为该点处Jacobi 矩阵的特征值[10].

扩展方程法是一种适用于高维分岔问题的直接求解方法，而且能同时获得分岔点及其特征.对于单向压缩屈曲问题，可采用扩展方程为[9]

伪弧长法是一种具有大范围收敛性的间接延拓方法，在分岔点附近对初始值的选取要求不高.式（12）则可进一步化为常微分方程的Cauchy 问题[12]：

式（28）为Euler 预报格式，式（29）为Newton 修正格式，迭代序列收敛于解曲线y(s)上的某一点，DG(yk)则为预报点yk处的Fréchet 导数，DG的表达式为

值得指出的是，扩展方程中的特征向量是求解分岔方向的前提，而分岔方向是进行解支转换的前提，联合使用扩展方程法和伪弧长法有利于开展大范围的后屈曲行为追踪来获取较为真实的失稳过程.

对于多参数屈曲问题，例如px和py双向压缩矩形薄板，可采用比例加载的方式求解临界参数，给定λx，λy=kλx，则临界参数为λx,cr，λy,cr=kλx,cr，通过改变比例系数k可得双参数平面上的相关曲线.平衡状态稳定性由Lagrange 定理判定，即Jacobi 矩阵为负定矩阵.

3 数值算例与讨论

3.1 Euler 屈曲算例

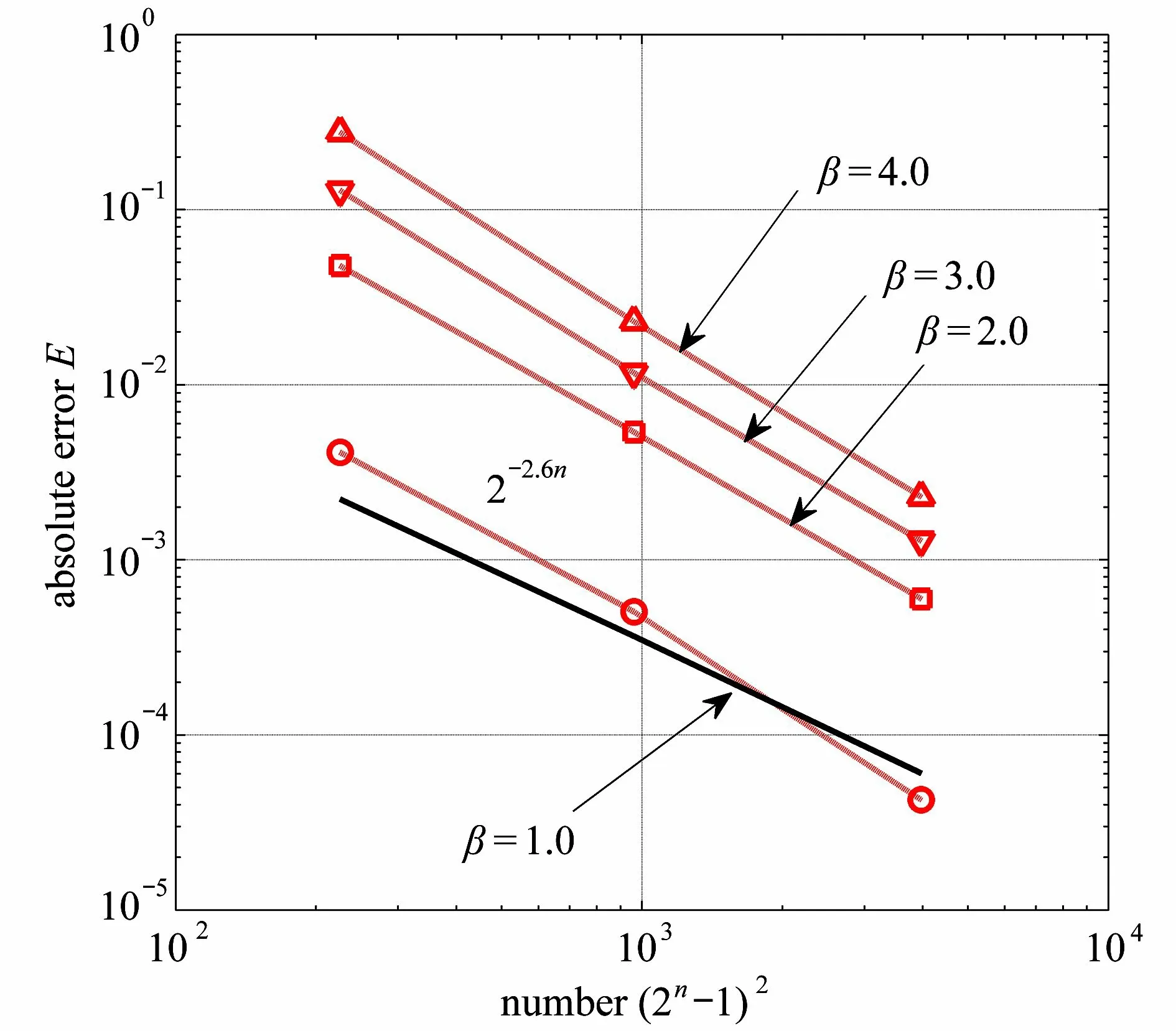
图1 四边简支板屈曲载荷的收敛阶数Fig.1 Convergence orders of buckling loads for 4-edge simply supported plates

对于方形板，四边简支情形的后屈曲平衡路径由二次摄动法获得[7]，四边固支情形由非线性有限单元法和基于Bior 3.1 的小波Galerkin 法获得其后屈曲平衡路径[6]，如图2所示.本文利用基于Coiflet 的小波Galerkin 法求得的后屈曲路径与上述结果是一致的，四边简支情形（m=n=4，5）两者的误差在最大挠度2 倍范围内误差不超过5%，四边固支情形（m=4）与已有结果的差别更小.基于Bior 3.1 的小波Galerkin 法涉及尺度函数的三重积分以及采用混合法处理边界，而基于Coiflet 的小波Galerkin 法仅仅需要计算尺度函数的二重积分.需要指出的是，Euler 后屈曲分析中通常假设模态的波形不变，因此其分析范围不宜取得过大.

图2 方形薄板单向压缩的后屈曲路径：(a)四边简支；(b)四边固支Fig.2 Post-buckling paths of square plates under uniaxial compression:(a)4-edge simply supported;(b)4-edge fixed

3.2 二次屈曲算例

Euler 屈曲系数按大小顺序记为ki,i=1,2,···.最小特征值k1附近，平凡解由稳定变为不稳定，高阶特征值ki(i>1)附近，平凡解均为不稳定.从ki处出发的非平凡解支上仍然有可能发生稳定性的变化，记该解支上的二次屈曲系数为ki2.本文采用拓展方程（26）直接求解二次屈曲临界载荷，分解尺度分别取(m，n)=(4,4)，(5,4)，(5,5)和(6,5)时的方形薄板屈曲系数如图3所示，表明小波Galerkin 法在求解二次屈曲临界载荷时仍然具有良好的一致性.

图3 四边固支方形薄板的二次屈曲系数Fig.3 Secondary buckling coefficients of 4-edge fixed square plates

不同长宽比下单向受压四边简支矩形薄板的二次屈曲系数见表1，分解尺度取m=6，n=4.表中结果显示：对于β=2.0 的简支板，屈曲系数k1=4.0，比值k12/k1和k22/k1分别为2.78 和1.34；对于β=2.0 的固支板，屈曲系数k1=7.467，比值k12/k1为6.15.β=2.0 的铝板受压屈曲实验则显示，简支板在加载压力为初始临界压力1.3 倍左右时屈曲波形由两个半波迅速跳跃成三个半波，固支板从一开始就出现三个半波，直至出现塑性破坏也没有出现波形跳跃现象[2].由半解析半经验公式可得，β=2.0 简支板和固支板的平均破坏应力与Euler 屈曲应力的比值分别为5.3 和3.5[14].可见，若k12对应的二次临界载荷小于屈曲破坏载荷，则实验能观察到波形跳跃现象，不过观察到的是不稳定非平凡解支上的失稳点，即k22.这是由于波形跳跃是一个变化迅速的动态过程.Nakamura 和Uetani 获得的长宽比为2 简支板的二次屈曲系数为12.45，更接近k12，这是由于其判定条件为稳定的非平凡解支失稳[8].由非线性有限元获得固支方板的k12和k22的值分别为17.46 和12.53，与本文结果也较为一致[12].

表1 单向受压弹性矩形薄板的二次屈曲系数Table 1 Secondary buckling coefficients of rectangular plates under uniaxial compression

为了确定波形跳跃的具体途径，还应了解不同屈曲模态之间的耦合，因此需要开展更大范围内的后屈曲平衡路径分析.对于长宽比为1.0 和2.0 的四边简支和四边固支矩形薄板，联合使用扩展方程和伪弧长法获得了大范围的后屈曲平衡路径追踪并进行了稳定性判定，分别如图4 和5所示.结果显示，k12处既可能发生超临界分岔也可能发生亚临界分岔，k22处则一般为亚临界分岔.四边固支方形薄板的大范围后屈曲路径最为典型，k12处和k22处均发生亚临界分岔且k12和k22之间存在连续的不稳定解，这个不稳定的解为前两阶模态的耦合，且投影到位移-转角组成的平面上为一条闭合曲线.长宽比为2.0 的四边固支板和简支板，k12处分别发生亚临界分岔和超临界分岔.

图4 四边简支薄板二次屈曲平衡路径：(a)β=1.0；(b)β=2.0Fig.4 Secondary buckling paths of 4-edge simply supported plates:(a)β=1.0;(b)β=2.0

图5 四边固支薄板二次屈曲平衡路径：(a)β=1.0；(b)β=2.0Fig.5 Secondary buckling paths of 4-edge fixed plates:(a)β=1.0;(b)β=2.0

大量的数值计算表明，从初始屈曲到二次屈曲的平衡路径可分为两种情形：一类是随着载荷幅值增大，屈曲波形不发生改变，只发生波形幅值增长，如图6 给出的方形薄板平衡曲面就是这种情形；一类是随着载荷增大，屈曲波形和幅值均发生变化，如图7 给出的β=2.0 矩形薄板平衡曲面则是这种情形.表1 中二次屈曲系数k12的值超过30 的矩形薄板，其二次屈曲附近的屈曲波形均会发生变化，即出现相邻稳定屈曲波形的耦合波形.最后考虑了双向压缩k=0.2 下四边固支方板的二次屈曲路径，如图8所示，可见载荷变化也使得屈曲模态的耦合通道不再闭合.

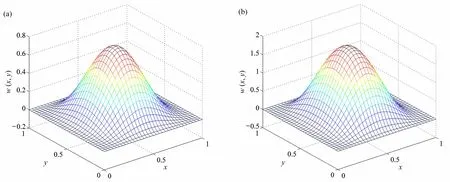
图6 方形薄板（β=1.0）后屈曲平衡曲面：(a)λ=110；(b)λ=159.991Fig.6 Equilibrium surfaces of square platesβ=1.0）on postbuckling paths:(a)λ=110;(b)λ=159.991

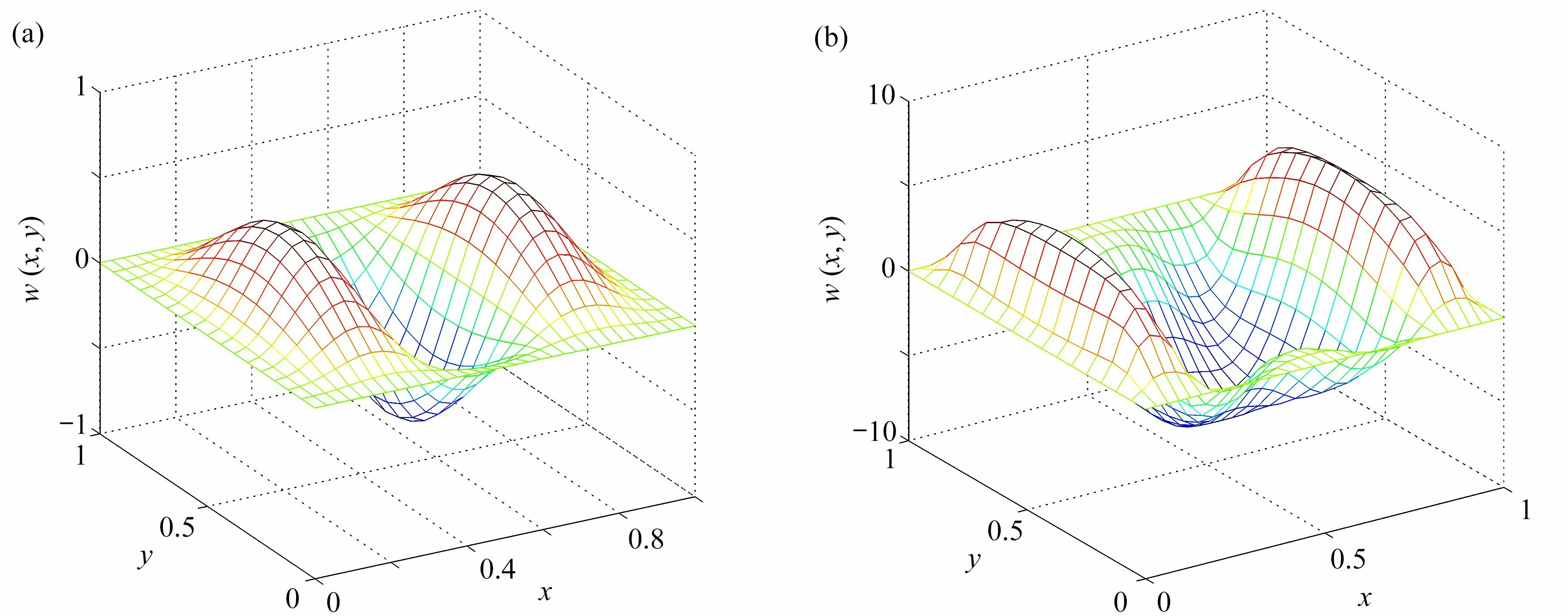
图7 矩形薄板（β=2.0）后屈曲平衡曲面：(a)λ=350；(b)λ=1811.765Fig.7 Equilibrium surfaces of rectangular plates (β=2.0)on postbuckling paths:(a)λ=350;(b)λ=1811.765

图8 加载比例k=0.2 四边固支方板双向压缩的二次屈曲路径Fig.8 Secondary buckling paths of a 4-edge fixed square plate with load ratio k=0.2

4 结论

本文开展了基于Coiflet 的小波Galerkin 法在矩形薄板二次屈曲问题中的应用研究，并给出了一个非线性屈曲方程Jacobi 矩阵的简便计算方法.数值计算结果表明：

1）基于Coiflet 的小波Galerkin 法在求解屈曲临界载荷时仍然具有较好的收敛性，且与稳定性实验结果一致；

2）在小范围后屈曲平衡路径追踪方面，小波Galerkin 法与摄动法和有限单元法等现有结果也是一致的；

3）完善矩形薄板二次屈曲的多参数大范围分析表明，在长宽比、边界条件和双向压缩载荷的影响下其前两阶屈曲模态的闭合耦合通道较为少见，矩形薄板后屈曲状态之间的跳跃可能会涉及更高阶的稳定模态.

附录

文献[2,13]中建立的基于Coiflet 尺度函数的修正基函数表达式为

修正系数为

引入 β0和 β1是为说明边界条件的施加过程，为了满足x=0 处的齐次边界，仅仅需要令β0,i=0，而其他元素保持不变即可.根据四点Malkov 数值微分公式推导了 ζ0和 ζ1：