一般宏观应力状态下凹角蜂窝结构的屈曲性能分析*

周世奇，侯秀慧,2，邓子辰,2

（1.西北工业大学 力学与土木建筑学院，西安 710129；2.复杂系统动力学与控制工业和信息化部重点实验室，西安 710072）

引言

蜂窝是典型的多孔材料，这种材料以平面内单元的二维排列和面外方向平行堆叠的周期性拓扑分布为特征.单胞相互连接形成的网络结构使得蜂窝相较于其他材料具有更高的孔隙率和更低的相对密度，这也导致了更高的比刚度强度和比能量吸收.单胞的拓扑结构可以显著地影响这种超轻材料的力学性能.因此，合理设计的微观结构使蜂窝具有一些超结构属性，比如负Poisson 比[1]、负热膨胀[2]、负刚度[3]等.这些特殊的性质源于蜂窝不同的微观几何拓扑，而不是构成蜂窝的基体材料.例如将传统正六边形蜂窝结构的凸形胞壁替换为凹形胞壁，可以得到相应的负Poisson 比特性，即结构在张力作用下纵向和横向双向膨胀而在压力作用下纵向和横向双向收缩.其他拉胀蜂窝结构还包括双V 形[4]、手性[5]和星形[6-7]胞元等，其中凹角蜂窝结构作为最简单也是最经典的拉胀蜂窝，受到了广泛的关注.以往的研究大多是基于凹角蜂窝基本的物理力学行为，如压缩[8]、冲击[9-10]、热学[11]、光学[12]以及声学[13]等领域的应用.如Hou 等[14]研究了凹角六边形蜂窝的能量吸收特性，与传统蜂窝相比，凹角六边形蜂窝具有更高的吸能效率.而在低速准静态压缩荷载作用下，蜂窝结构的胞壁会发生屈曲破坏从而丧失稳定性.

已有研究表明，蜂窝结构在压缩载荷作用下发生屈曲的特性，并不总是作为一种结构缺陷的存在.蜂窝结构的微观不稳定模式作为一种调制周期性结构宏观力学性能的方法已经被广泛采用，比如手性、波传播、声子特性以及光学特性等.Bertoldi 等[15]揭示了多胞结构由于弹性失稳而产生负Poisson 比效应的机理.Yang等[16]利用多胞结构的屈曲提出了一种屈曲致动器用于制作软体机器人.由此可知，对蜂窝结构的屈曲分析尤其是凹角蜂窝这种拉胀蜂窝的屈曲分析是十分必要的.Jiménez 和Triantafyllidis[17]研究了矩形和正六边形蜂窝在轴向压缩和横向剪切组合荷载作用下的屈曲，发现屈曲模式高度依赖于载荷类型.Combescure 等[18]利用群论方法研究了有限应变圆形蜂窝的变形模式及其稳定性.梁观坡等[19]基于数值模拟和理论分析研究了含周期性椭圆孔二维结构的屈曲行为，研究发现改变孔的几何参数，椭圆孔结构的屈曲模态随之发生转换.Peng等[20]将变分渐近法扩展到凹角蜂窝夹层板的面外屈曲研究，得出在相同条件下，凹角蜂窝夹层板的屈曲载荷大于传统的蜂窝夹层板.Gavazzoni 等[21]基于材料和几何非线性以及制造缺陷之间的耦合作用，研究了软多胞结构局部不稳定性的循环响应.然而，却少见针对负Poisson 比凹角蜂窝结构面内屈曲模态力学性能的研究报道.

本文系统研究了凹角蜂窝的面内屈曲特性，在第1 节中，建立了凹角蜂窝的有限元模型，对凹角蜂窝在单轴压缩下的屈曲行为进行了数值模拟.以此为基础，在第2 节中建立了凹角蜂窝对应于不同屈曲模态的屈曲强度解析公式，揭示凹角蜂窝不同屈曲模态的产生机理.随后，在第3 节中通过实验，对以上数值模拟和理论分析结果进行了验证.

1 有限元分析

利用有限元软件ABAQUS 对凹角蜂窝在宏观应力下的屈曲进行模拟.建立的有限元模型在水平方向上设置5 个胞元，在竖直方向上设置7 个胞元，将胞壁材料设置为理想的弹塑性模型，质量密度为1230 kg/m3，弹性模量为35 MPa，Poisson 比为0.45.有限元模型是三维壳结构，为了研究凹角蜂窝面内屈曲性能，限制模型的面外位移和旋转.构造的三维凹角蜂窝模型胞壁的面内长细比均大于1/10，受力情况类似于板壳结构，实体单元在模拟板壳结构时容易形成剪力自锁从而影响计算结果，所以本文在进行凹角蜂窝面内屈曲的有限元模拟时采用壳单元.模拟沿着平行于水平胞壁和垂直于水平胞壁方向的准静态压缩时，在模型底部的每一个节点上设置固定约束限制模型底部的线位移和转角位移.在模型顶部的每一个节点上设置滑动约束限制模型顶部的水平位移和转角位移，如图1所示.为了描述方便，将平行于水平胞壁和垂直于水平胞壁的方向分别定义为x方向和y方向.用X=σx/(E(t/L)3)和Y=σy/(E(t/L)3)分别表示沿着x方向和y方向的应力系数.X=0,Y=1表示沿着y方向的单轴压缩，X=1,Y=0表示沿着x方向的单轴压缩.

图1 凹角蜂窝的有限元模型和边界条件：（a）沿着x 方向准静态压缩的边界条件；（b）沿着y 方向准静态压缩的边界条件Fig.1 The finite element model and boundary conditions for the re-entrant honeycomb:(a)boundary conditions for the quasi-static compression along the x direction;(b)boundary conditions for the quasi-static compression along the y direction

对凹角蜂窝有限元模型划分网格时，网格类型设置为S4R，该单元类型是通用的壳单元类型，并且这种单元类型既适用于薄壳结构，也适用于厚壳结构，比较适合用来计算凹角蜂窝这种胞壁长细比不同的结构.为了确定网格的全局尺寸，进行了收敛性分析.收敛性分析选用的有限元模型的几何设置、材料属性、边界条件和加载条件与前文所述的有限元模型保持一致.根据图2所示的收敛性计算结果，网格尺寸设置为5 mm，4 mm，3 mm 时，计算结果误差较大；网格尺寸为2 mm 时，曲线开始趋于平缓.为确保有限元模拟结果最终收敛，我们计算了网格尺寸为1 mm，0.5 mm，0.3 mm，0.2 mm，0.1 mm 的情况，发现网格尺寸为0.5 mm，0.3 mm，0.2 mm，0.1 mm 时，计算结果基本一致，考虑到有限元模拟研究的简洁高效，将网格尺寸设置为0.5 mm.

图2 收敛性计算结果Fig.2 Convergence calculation results

图3 列出了凹角蜂窝在单轴压缩荷载作用下的前十阶屈曲模态.当凹角蜂窝承受沿着y方向的压缩载荷时（X=0,Y=1），前五阶屈曲模态的单胞变形是一致的，而整体屈曲模态表现为加载方向上的波峰数逐阶递增，这与单杆压缩的高阶屈曲模态类似[22].从第六阶开始出现不同的单胞变形，这是因为所选结构的尺寸达到所能承受的波峰数的极限从而导致多阶屈曲模态偶连.当凹角蜂窝承受沿着x方向的压缩载荷时（X=1,Y=0），前八阶屈曲模态的单胞变形保持一致，而整体屈曲模态没有观察到波峰数递增的现象.从第九阶开始出现不同的单胞变形，同样考虑是多阶屈曲模态偶连导致的.因此分别提取第一阶模态进行理论分析，将沿着x方 向准静态压缩得到的屈曲模态命名为屈曲模态Ⅰ，沿着y方向准静态压缩得到的屈曲模态命名为屈曲模态Ⅱ，如图4所示.

图3 凹角蜂窝在单轴荷载作用下的前十阶屈曲模态：（a）沿着y 方向单轴压缩；（b）沿着x 方向单轴压缩Fig.3 The 1st 10 buckling modes of the re-entrant honeycomb under uniaxial loading:a）uniaxial compression along the y direction;（b）uniaxial compression along the x direction

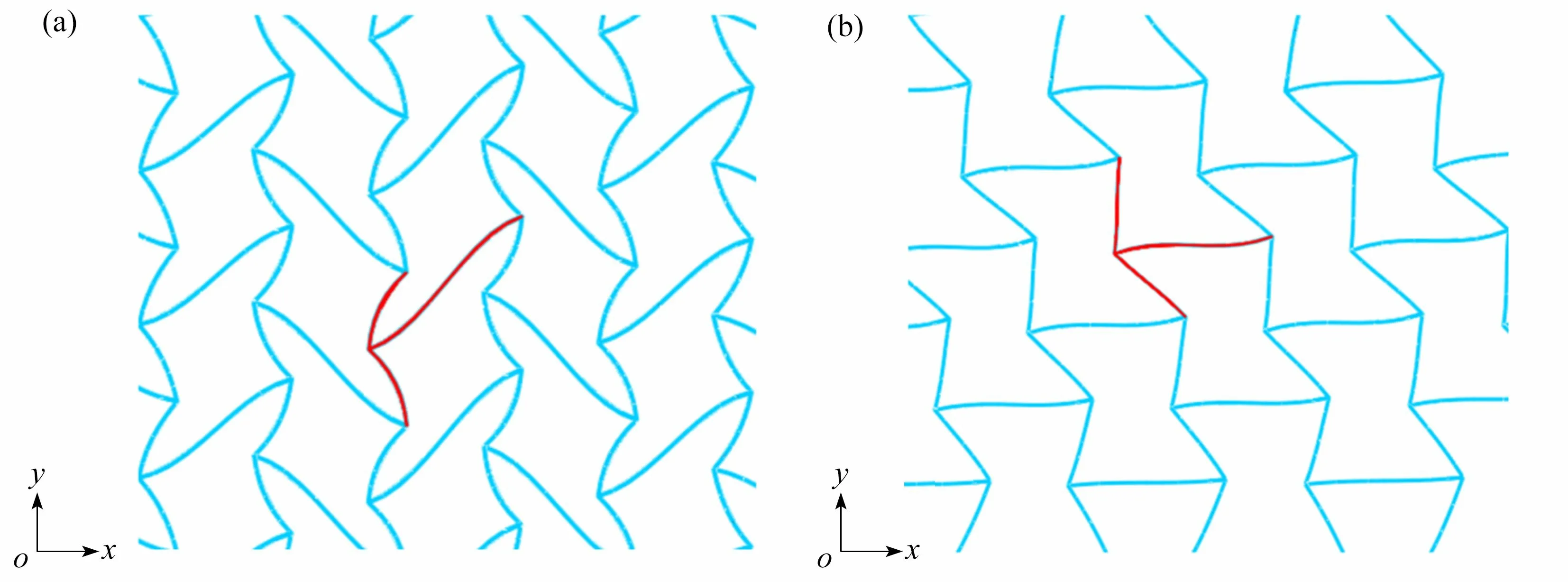
图4 凹角蜂窝的第一阶模态：（a）沿着x 方向准静态压缩得到屈曲模态Ⅰ；（b）沿着y 方向准静态压缩得到屈曲模态ⅡFig.4 The 1st buckling modes of the re-entrant honeycomb:(a)buckling mode Ⅰ obtained under quasi-static compression along the x direction;(b)buckling mode Ⅱ obtained under quasi-static compression along the y direction

为了研究尺寸效应对凹角蜂窝的屈曲模态和屈曲强度的影响，设置了三种不同胞元数量的凹角蜂窝模型：3 × 4 构型、5 × 7 构型、7 × 10 构型，第一个数字代表水平方向的胞元数量，第二个数字代表竖直方向的胞元数量.这三种构型的面内长宽比均等于1，这样就排除了面内长宽比对凹角蜂窝屈曲行为的影响.结果表明：三种构型的一阶屈曲模态是相同的；随着胞元数量的增加，单胞变形模态转变的现象会得到延缓，如图3和图5所示；凹角蜂窝的胞元数量对屈曲强度的影响可以忽略不计，如图6所示，因此后续研究采用5 × 7 构型.

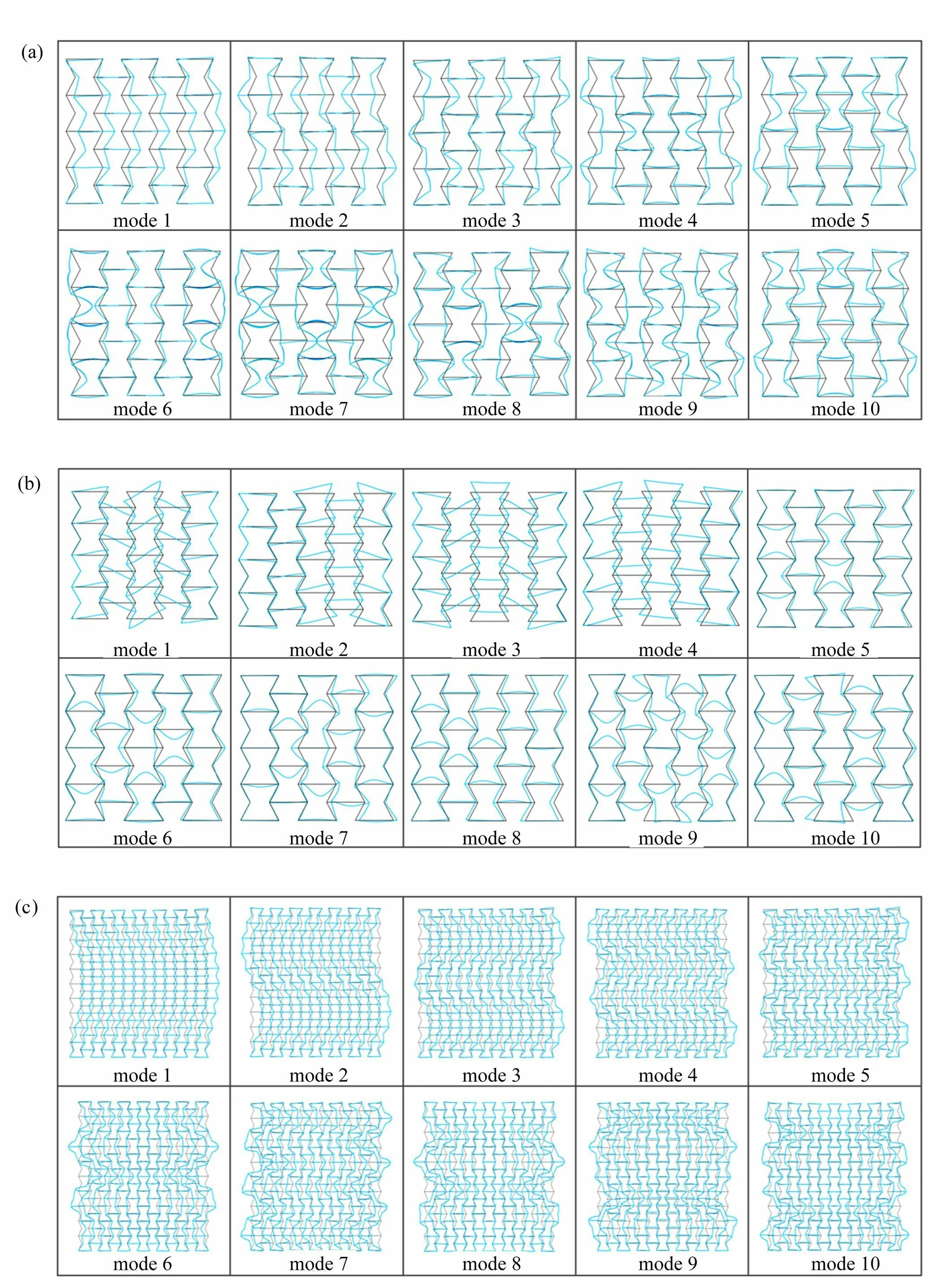
图5 不同单胞数量的凹角蜂窝的屈曲模态：(a)3×4 构型沿着y 方向单轴压缩；(b)3×4 构型沿着x 方向单轴压缩；(c)7×10 构型沿着y 方向单轴压缩；(d)7×10 构型沿着x 方向单轴压缩Fig.5 Buckling modes of the re-entrant honeycomb with different numbers of unit cells:(a)the 3×4 configuration under uniaxial compression in the y direction;(b)the 3×4 configuration under uniaxial compression in the x direction;(c)the 7×10 configuration under uniaxial compression in the y direction;(d)the 7×10 configuration under uniaxial compression in the x direction

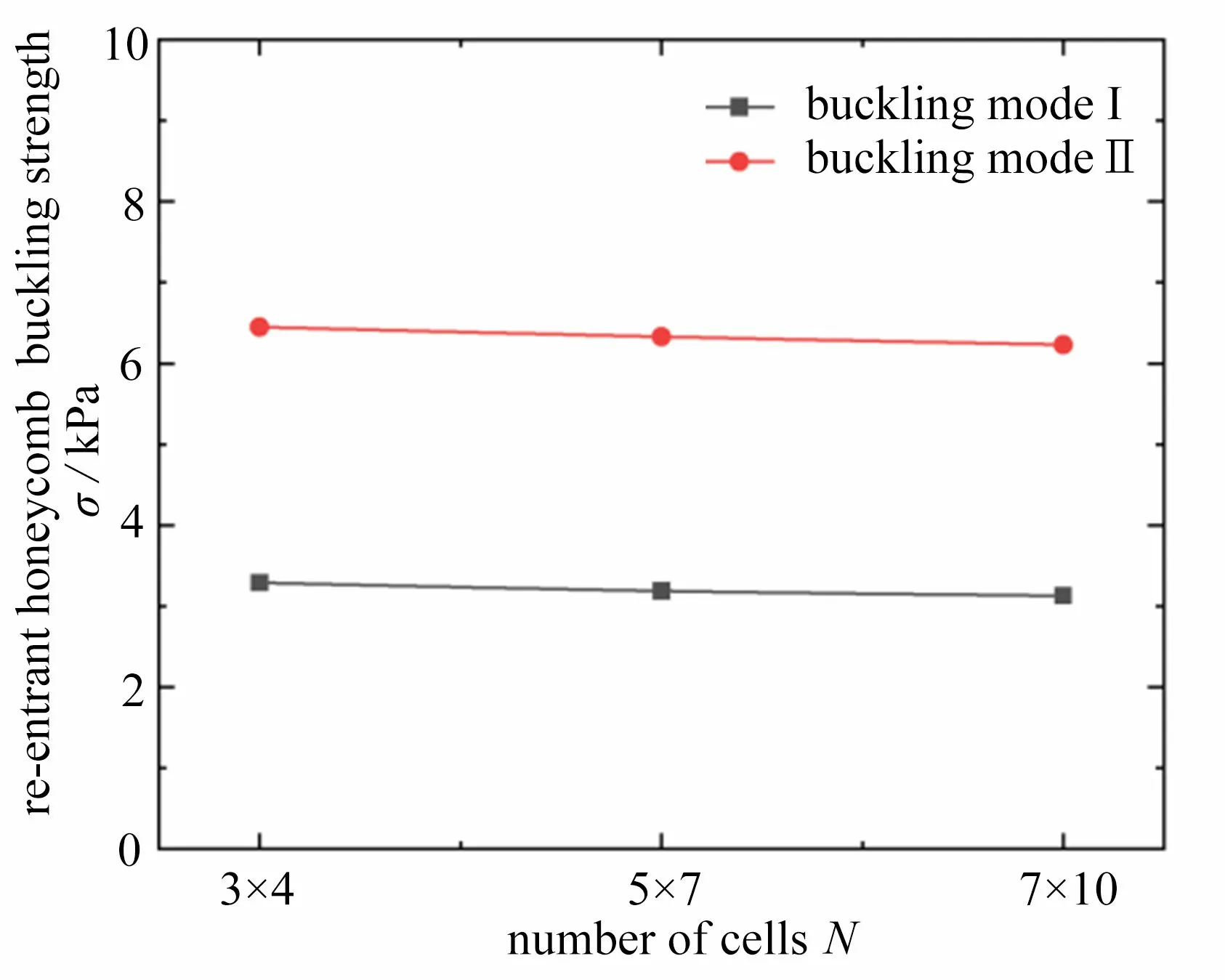
图6 不同单胞数量的凹角蜂窝的屈曲强度Fig.6 Buckling strengths of the re-entrant honeycomb with different numbers of unit cells

2 理论分析

通过有限元模拟凹角蜂窝在不同加载方式下的屈曲行为，分别获得凹角蜂窝沿着x方向和y方向的单轴压缩屈曲变形模式，并从中提取具有代表性的单胞变形模式为理论分析模型（图4）.依据 Timoshenko 和Gere 提出的梁柱理论[23]，构建承受轴力作用的杆件杆端弯矩和杆端转角位移的关系.即梁柱结构在轴向力P作用下，当其外荷载为一对顺时针杆端弯矩Ma和Mb时（见图7，下标a和b分别对应杆件的两端结点），梁柱的杆端转角θa和 θb可以使用梁柱方程计算得到：

图7 梁柱的杆端转角和杆端弯矩Fig.7 End rotations and end bending moments of the beam-column

利用梁柱理论公式对凹角蜂窝单胞的每一个胞壁的杆端弯矩和转角位移建立相应的梁柱方程，对于具有杆端线位移的胞壁还需建立弯矩平衡方程.将这些方程用统一的矩阵公式表示，根据屈曲临界条件，即相应位移不全为零，可得方程组的系数矩阵的行列式为零，解行列式得凹角蜂窝屈曲稳定方程.

2.1 屈曲模态Ⅰ

凹角蜂窝整体与胞元的应力状态和几何结构如图8所示，水平杆的长度为La，斜杆的长度为Lb，水平杆和斜杆的夹角为θ，面外厚度为c.对于任意的应力 σx和 σy，可等效为水平杆和斜杆上的集中力F，P和W，分别为

图8 一般宏观应力状态下的凹角蜂窝结构：（a）凹角蜂窝整体的几何结构和应力状态；（b）基础单胞的几何结构和应力状态Fig.8 The re-entrant honeycomb structure under a general macroscopic stress state：(a)the geometric structure and the stress state of the re-entrant honeycomb;(b)the geometric structure and the stress state of the unit cell

由式（2）可得OA，OB和OC杆的轴力分别为Fa，Fb和Fc：

这里轴力的符号规定为压力为正，拉力为负.从有限元模拟的屈曲模态图4（a）中提取凹角蜂窝的胞元屈曲模态如图9所示，虚线表示屈曲前的位置，实线表示屈曲后的位置.由于OA杆的屈曲变形是中心对称的,所以OA杆两端的弯矩大小和方向均相等，而OB，OC杆的屈曲变形是关于过杆中点的法线对称的，所以OB，OC杆两端的弯矩大小相等方向相反.OA杆两端有相对线位移，而OB，OC杆没有.

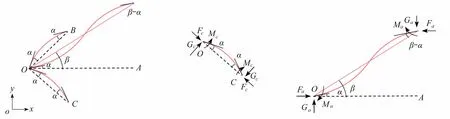
图9 凹角蜂窝屈曲模态Ⅰ的单胞模态和OA，OC 杆的内力示意图Fig.9 The unit cell modes for buckling mode Ⅰ of the re-entrant honeycomb and the internal forces of rods OA and OC

将OA，OB和OC三根杆的梁柱理论关系表达式以及OA杆的弯矩平衡方程表示为式（5）中的矩阵形式：

其中前三行分别表示OA，OB和OC杆的梁-柱理论关系式，第四行表示O点的力矩平衡，第五行表示OA杆关于O点的力矩平衡.式（5）中方程的非齐次项不包含杆端弯矩、杆端转角和轴力，所包含的剪力只会引起静态挠度而非屈曲，不影响系数矩阵的结果.

由图9 可知，当发生屈曲时，α和β不全为0，故式（5）中的方程组存在非零解，系数行列式等于零.

化简后可得

即

式 (8)是关于qa，qb和qc的关系式，表示凹角蜂窝在宏观应力状态下产生屈曲模态Ⅰ的应力条件.

2.2 屈曲模态Ⅱ

从有限元模拟的屈曲模态图4（b）中提取凹角蜂窝的胞元屈曲模态如图10所示，虚线表示屈曲前的位置，实线表示屈曲后的位置.由于每根杆的屈曲变形是中心对称的，所以OA杆两端的弯矩大小和方向均相等，OB和OC杆同理.OB，OC杆两端有相对线位移，而OA杆没有，这与屈曲模态Ⅰ不同.

将OA，OB和OC三根杆的梁柱理论关系表达式以及OB和OC杆的弯矩平衡方程表示为式（9）中的矩阵形式：

其中前三行分别表示OA，OB和OC杆的梁-柱理论关系式，第四行表示O点的力矩平衡，第五行表示OB杆关于O点的力矩平衡，第六行表示OC杆关于O点的力矩平衡.

由图10 可知，当发生屈曲时，α和β不全为0，故式（9）中的方程组存在非零解，系数行列式等于零.

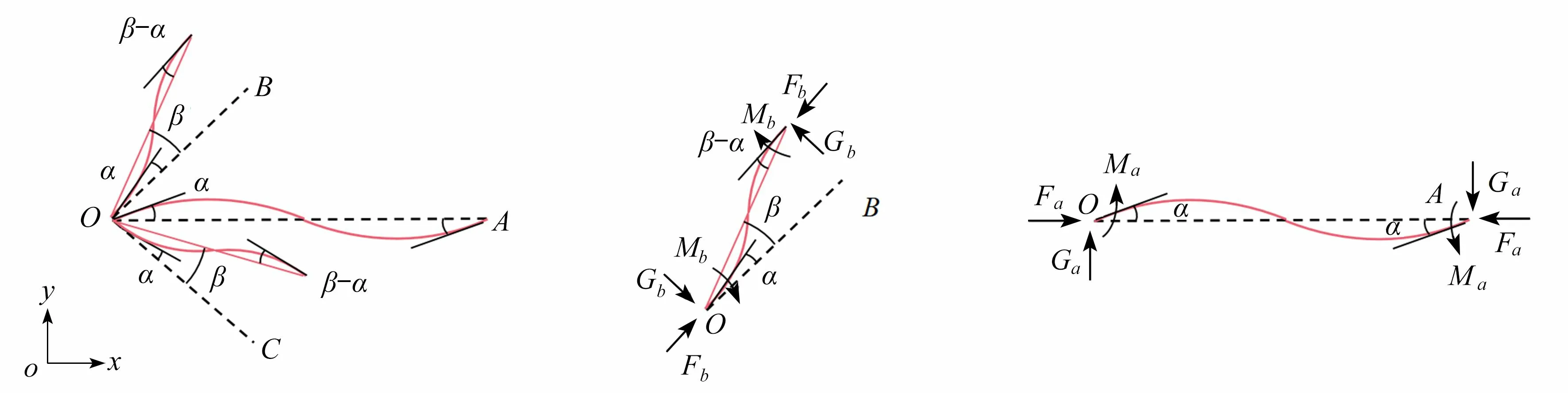
图10 凹角蜂窝屈曲模态Ⅱ的单胞模态和OA，OB 杆的内力示意图Fig.10 The unit cell modes for buckling mode Ⅱ of the re-entrant honeycomb and the internal forces of rods OA and OC

化简后可得

即

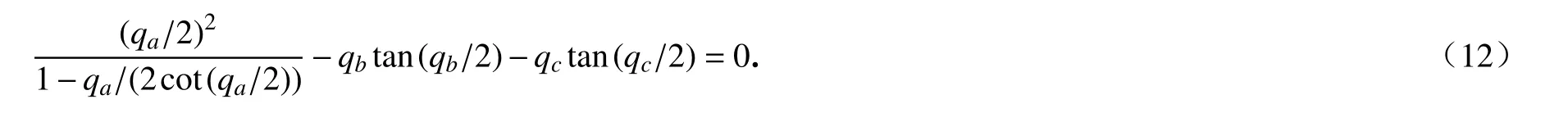
式(12)是关于qa，qb和qc的关系式，表示凹角蜂窝在宏观应力状态下产生屈曲模态Ⅱ的应力条件.

2.3 理论结果分析

根据式（8）和式（12）的关系绘制曲线，如图11所示.图11 给出了凹角蜂窝在宏观应力状态下屈曲模态Ⅰ和屈曲模态Ⅱ对应的应力关系，水平轴和竖直轴分别代表无量纲化的宏观应力，分别用X=σx/(E(t/L)3)和Y=σy/(E(t/L)3)表示.点线代表屈曲模态Ⅰ，点划线代表屈曲模态Ⅱ.

图11 凹角蜂窝屈曲模态Ⅰ和Ⅱ的失效界面Fig.11 Failure surfaces for buckling modes Ⅰ and Ⅱ of the re-entrant honeycomb

两条曲线的交点出现在第一象限，在交点右边的区域，同样的Y值，屈曲模态Ⅰ的X值小于屈曲模态Ⅱ的X值.在这块区域包含的任意应力状态下，凹角蜂窝的屈曲模态为屈曲模态Ⅰ.在交点左边的区域，同样的X值屈曲模态Ⅱ的Y值小于屈曲模态Ⅰ的Y值.在这块区域包含的任意应力状态下，凹角蜂窝的屈曲模态为屈曲模态Ⅱ.也即表明，当沿着x方 向的应力为主应力时，凹角蜂窝的屈曲变形呈现为屈曲模态Ⅰ；当沿着y方向的应力为主应力时，凹角蜂窝的屈曲变形呈现为屈曲模态Ⅱ.凹角蜂窝在双轴应力状态下的优先屈曲模式对双轴应力的比例关系表现出敏感性.同时我们还发现，点划线延伸至第三象限，这表明凹角蜂窝在双轴拉伸的应力状态下依然会发生屈曲变形，而传统正六边形蜂窝仅在受压的状态下才会发生屈曲变形，这可归结为凹角蜂窝不同于一般蜂窝的凹角几何特征所引起的拉胀效应.根据图11 可得凹角蜂窝在x方向单轴压缩下的屈曲强度为σx/E=0.076(t/L)3（图11 中三角形标注），在y方向单轴压缩下的屈曲强度为σy/E=0.158(t/L)3（图11中菱形标注），分别对应着在单轴压缩下屈曲模态Ⅰ和屈曲模态Ⅱ的屈曲强度.这个结果表明屈曲模态Ⅰ的屈曲强度低于屈曲模态Ⅱ的屈曲强度，因此屈曲模态Ⅰ可认定为整体屈曲模态，屈曲模态Ⅱ可认定为局部屈曲模态.，

3 实验

3.1 实验设置

采用增材制造技术制备实验样本，3D 打印机型号为RAISED3D E2，打印材料采用PolyFlex TPU95A.样本的长宽高为129.8 mm×129.2mm×18.3mm，单胞水平杆长度为18.3mm，斜杆长度为10.2mm，水平杆和斜杆的夹角壁厚为1 mm，打印层厚为0.025mm.实验样本如图12所示.使用万能试验机分别对实验样本沿着x方向和y方向进行准静态压缩实验.行程位移设置为20 mm，压缩速度设置为1 mm/min，温度设置为23 ℃，可认定为常温条件下的准静态压缩.

图12 凹角蜂窝沿着x方向和y 方向单轴压缩的实验结果和数值结果对比Fig.12 Comparison of experimental and numerical results of re-entrant honeycombs under uniaxial compression along the x and y direction

3.2 实验结果和理论研究、数值研究的对比

图12 展示了凹角蜂窝结构在准静态压缩条件下的变形情况.提取实验结果中凹角蜂窝完全屈曲变形的模态图与第1 节中有限元模拟的屈曲模态进行对比，发现凹角蜂窝结构的整体屈曲变形模态和单胞屈曲变形模态在实验和有限元模拟中保持高度的一致性，如图12所示.实验结果表明凹角蜂窝沿着x方向单轴压缩时，屈曲变形模态表现为屈曲模态Ⅰ，而沿着y方向单轴压缩时，屈曲变形模态表现为屈曲模态Ⅱ，这与理论预测的结果一致.

从图13 中可以看到，实验样本分别承受沿着x方向和y方向的单轴压缩，在应变到0.039 时，沿着x方向压缩的应力-应变曲线由近似线性的弹性阶段过渡为平台阶段，即杆件开始发生屈曲变形；而沿着y方向压缩的应力-应变曲线的弹性阶段在应变到0.044 时才结束.根据应力-应变曲线，可以观察到在发生屈曲时，沿着y方向压缩的曲线会出现短暂的下降，随后呈现平台关系.且沿着y方向压缩的平台应力明显高于沿着x方向压缩的平台应力，也就是说凹角蜂窝沿着y方向的屈曲强度高于沿着x方向的屈曲强度，这与图11 的结果一致.将应力-应变曲线从弹性阶段结束过渡为稳定平台阶段的这部分应力的平均值视为屈曲应力，并与数值和理论研究得到的屈曲强度进行对比，如表1所示.结果表明理论计算的屈曲强度与实验和数值研究得到的屈曲强度存在一定的误差，理论结果略低于实验和数值研究的结果.这是因为理论研究是以凹角蜂窝单胞承受理想的应力状态为前提，即图8所示的一般应力状态，并将这种一般应力状态等效为单胞所受的集中荷载（即图8（b）中所示的P，W，F），以此构建的矩阵公式（5）和（9）.在实验和数值研究中凹角蜂窝所承受的荷载为均匀荷载，这就使得实验和数值研究得到的屈曲应力值与理论分析得到的应力值存在误差.同时，还可以看到实验和数值研究得到的屈曲应力值存在微小误差，这是因为数值研究中增加了限制凹角蜂窝面外位移的约束而导致的.

图13 凹角蜂窝沿着x方向和y方向单轴压缩的应力-应变曲线Fig.13 Stress-strain curves of the re-entrant honeycomb in uniaxial compression along the x and y directions

表1 实验、数值和理论研究得到的凹角蜂窝屈曲强度对比Table 1 Comparison of buckling strengths of re-entrant honeycombs obtained from experimental,numerical and theoretical studies

4 结论

通过有限元仿真分析发现了凹角蜂窝在宏观应力状态下的两种屈曲模态.为了研究这两种屈曲模态的屈曲强度以及产生的机理，本文采用梁柱理论对其进行了理论分析.根据梁-柱方程和平衡关系建立包含杆端弯矩和杆端转角的方程组，利用屈曲临界条件得稳定方程，进而得到屈曲强度的解析表达式.采用增材制造技术打印凹角蜂窝试件，进而对其屈曲性能进行实验验证.将理论结果与实验和有限元结果进行对比分析.结果表明，通过改变加载条件，分别获得凹角蜂窝的两种屈曲模态，即屈曲模态Ⅰ和屈曲模态Ⅱ.当双轴应力中x方向上的应力占据主导地位时，即σx>σy，凹角蜂窝优先产生屈曲模态Ⅰ.当双轴应力中y方向上的应力占据主导地位时，即σx<σy，凹角蜂窝优先产生屈曲模态Ⅱ.凹角蜂窝具有不同于一般蜂窝的凹角几何特征，从而产生了负Poisson 比效应；并且这种负Poisson 比效应使得凹角蜂窝在双轴拉伸的应力状态下依然会发生屈曲变形，而传统正六边形蜂窝却不会出现这种现象.本文提出的凹角蜂窝两种屈曲模态的稳定方程式(8)和(12)，能够有效预测凹角蜂窝在任意应力状态下的屈曲模式，对凹角蜂窝因失稳而破坏以及利用凹角蜂窝的屈曲实现特殊力学性能的研究具有一定的指导意义.