基于PDE灵敏度滤波器的算法研究*

孟换利，张岐良，王 杰

（1.中山大学 系统科学与工程学院，广州 510006；2.天津航天长征火箭制造有限公司，天津 300462）

引言

为应对越来越高的力学性能要求和越来越严酷的服役环境，在结构设计中应用拓扑优化技术已成为一种必然选择.在结构的概念设计阶段通过结构拓扑优化确定材料的最优布局形式，可以帮助设计者发现结构最佳的应力传导路径，从而以最少的材料实现最优的结构性能.Deaton 和Grandhi[1]调查了2000年至2012年连续体结构拓扑优化的研究现状与应用.Zhu 等[2]综述了面向增材制造的拓扑优化技术的典型应用场景、研究热点和挑战.卫志军等[3]对双隔板进行了拓扑优化，可以有效地抑制流体晃荡.

然而，连续体结构的拓扑优化结果往往存在棋盘格现象、数值不稳定等问题，Sigmund[4]以及Bruns、Tortorelli[5]使用的灵敏度滤波器和密度滤波器可以有效地解决上述问题.研究者们在此基础上发展了多种过滤方法，如灰度单元等效转换方法[6]、动态参数调整方法[7]和灰度单元分层双重惩罚方法[8]等.上述方法在一定程度上可以有效地抑制灰度单元、消除棋盘格现象，防止边界灰度扩散，但没有关注过滤效率.与通过获取邻域的单元信息来修正中心单元的灵敏度滤波器不同，PDE 滤波器的实质是将灵敏度过滤值表示成Neumann 边界条件下的Helmholtz 方程的解，其求解只需考虑有限元离散的网格信息，避免了占用大量内存，极大地提高了过滤效率.然而随着网格的不断细分，该滤波器的代数方程维数越来越高，采用以Gauss 消元法为基础的直接法求解，会导致耗时过长和内存需求量增加等问题，从而影响该滤波器的效率.此外，随着计算机性能的提高和算法技术的发展，精细的数值模拟成为可能，使得待求解的线性方程组的维数越来越高，研发高效的线性求解器加速算法[9-11]已变得至关重要.

多重网格是一种高效的求解算法，近期在偏微分方程参数反演问题方面有许多应用[12-13]，并广泛地应用到图像处理[14]、流体模拟[15]和结构拓扑优化[16-17]等领域.为提高大规模结构拓扑优化灵敏度过滤的效率，本文基于体积约束下柔度值最小的固体各向同性惩罚微结构(SIMP)插值模型，针对大规模PDE 灵敏度滤波器的求解问题，对其进行有限元分析得到代数方程，再采用共轭梯度算法、多重网格算法以及多重网格预处理共轭梯度算法进行求解，得到了过滤域的节点灵敏度值，通过节点到单元的映射得到了单元灵敏度过滤值.

1 优化模型

在变密度法中，SIMP 模型是目前工程领域应用最广泛的材料插值模型，为了使模型更具有代表性，基于SIMP 插值模型，建立在体积约束下柔度值最小的连续体结构拓扑优化模型：

其中，目标函数C为结构的总体柔度，F为力向量，U为位移，K为结构的总刚度矩阵，xi和ui是第i个单元的相对密度和节点位移，ki和k0是单元刚度矩阵，V是优化后的结构体积，V∗为结构体积约束，V0为整个设计域的初始体积，f为优化体积比，vi为第i个单元的体积，xmin和xmax为单元相对密度的最小和最大极限值，N为结构离散单元总数.

SIMP 法又称幂律法，其材料插值模型以密度为设计变量，单元材料弹性模量和密度之间的关系为

其中E0和Emin是固体和空洞部分的材料弹性模量，Ei为第i个单元插值后的弹性模量.

2 拓扑优化算法

2.1 总体框架

连续体结构拓扑优化实现流程如图1所示.首先，初始化优化参数：定义问题的设计区域、约束和载荷.其次，建立有限元模型：划分有限元网格，将结构离散化，建立式(1)所示的连续体结构拓扑优化数学模型.另外，有限元分析：计算刚度矩阵、节点位移、目标柔度值和灵敏度.之后，PDE 灵敏度过滤：解决数值不稳定问题和消除棋盘格现象.然后，采用二分法和OC 准则更新Lagrange 乘子和设计变量，判断是否满足体积约束条件：满足则输出设计变量；若不满足，则回到上一步再次更新Lagrange 乘子和设计变量.最后，检查是否满足收敛准则：若满足，则输出拓扑优化结果；若不满足，则再次进行有限元分析，进行下一轮迭代.

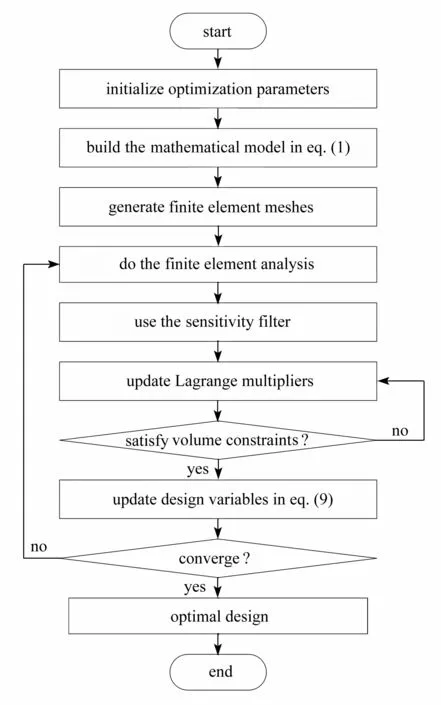
图1 基于SIMP 插值模型连续体结构拓扑优化实现流程图Fig.1 The flow chart of continuum structure topology optimization based on the SIMP interpolation model

为解决传统PDE 灵敏度滤波器过滤慢的问题，本文采用共轭梯度算法求解该滤波器的对称正定代数方程，为进一步解决网格数量增加导致系数矩阵维数增加和趋近最优解时，该算法收敛速度减缓的问题，结合多重网格可以均匀衰减误差，加快算法收敛速度的优点，使用多重网格算法和预处理共轭梯度算法求解该方程，提升过滤效率.此外，在预处理共轭梯度算法中，采用多重网格预处理降低系数矩阵的条件数.

2.2 PDE 灵敏度滤波器

本文采用PDE 灵敏度滤波器[18-19]，其核心思想是将过滤域的节点灵敏度值隐式表示为具有Neumann 边界条件的Helmholtz 方程的隐式解，然后通过节点到单元的映射得到单元灵敏度过滤结果：

2.3 PDE 灵敏度滤波器的求解

PDE 灵敏度滤波器的实质是以Neumann 边界为条件的Helmholtz 偏微分方程，其求解步骤如下：

第1 步 有限元离散得到Helmholtz 方程(3)的代数方程：

其中KF是标量问题的标准有限元刚度矩阵，TF是将单元相对密度映射到具有节点值的向量的矩阵.针对代数方程(5)的系数矩阵是对称正定稀疏病态的特点，本文拟采用共轭梯度算法、多重网格算法和多重网格预处理共轭梯度算法求解该代数方程，从而得到过滤区域内的节点灵敏度值.

第2 步 通过对过滤域的节点灵敏度值映射得到单元灵敏度过滤值：

2.3.1 多重网格算法

在固定网格中采用常规的迭代方法求解线性方程组，初始时收敛速度很快，趋近最优解时，收敛速度慢，计算时间长.采用Fourier 级数表示误差，得到两种不同的误差：波长较短、波形频率高的高频分量误差和波长较长、波形频率低的低频分量误差.由于波形频率的高低是相对的，把细网格中的低频波形放到粗网格中就有可能变成高频波形.因此采用多重网格来消除误差分量，使各种频率的误差得到比较均匀的衰减，从而加快迭代收敛速度.假设有L重网格，k=1 为最细的网格层，在k层上的多重网格迭代解，多重网格V 循环具体过程如下（伪代码见算法1）：

步骤1 前光滑.采用常规的迭代方法消除误差高频分量，具体步骤为：在细网格上，采取2 ～ 3 次的阻尼Jacobi 迭代方法得到线性方程组的近似解.迭代公式的通式为

其中Sk为光滑子，Sk=ωDk，ω 为阻尼因子，Dk为Ak的主对角元素矩阵.

步骤2 粗网格校正.计算在粗网格上误差的近似解，具体步骤为：首先计算细网格上的残差然后使用限制算子把细网格上的残差限制到粗网格上，得到粗网格上的残差最后根据网格的层数求解线性方程组得到粗网格上误差的近似解，若是最粗的网格层，则利用直接法求解否则利用多重网格V 循环求解其中粗网格算子Ak+1取Galerkin 算子.

步骤3 插值.计算细网格上的解，具体步骤为：先使用插值算子把粗网格上的近似误差插值到细网格上然后使用公式得到在细网格的解.本文采用的插值算子为

步骤4 后光滑.为保证整个迭代对称，在细网格上，采取具有相同参数的阻尼Jacobi 迭代法求解线性方程组.

算法1

2.3.2 多重网格预处理共轭梯度算法

考虑到代数方程的系数矩阵是大型、稀疏、对称正定的，有时甚至为病态的，则重点研究了多重网格预处理共轭梯度算法（伪代码见算法2），采用多重网格作为预处理方法降低系数矩阵的条件数.

算法2

2.4 设计变量的更新

优化准则法（OC 准则）具有收敛速度快、易于实现等特点.本文采取OC 准则求解优化模型(1)，基本思路为，先引入Lagrange 乘子把约束问题(1)转化为无约束问题，再根据极值点存在的条件即K-T 条件以及不动点迭代得到设计变量的迭代公式为

2.5 收敛准则

包括外循环和内循环，外循环包括有限元分析和更新单元灵敏度，迭代收敛条件如下：

内循环包括更新设计变量、Lagrange 乘子和过滤域的节点值.采用二分法和OC 准则更新Lagrange 乘子和设计变量，以满足模型(1)中的体积约束和设计变量的边界约束，迭代收敛条件如下：

其中η为收敛控制因子，l2和l1为较大和较小的Lagrange 乘子.采用共轭梯度算法、多重网格算法以及多重网格预处理共轭梯度算法求解代数方程，构造迭代收敛准则为

其中τ为收敛控制因子，rk和r0为第k次和初始时代数方程的残量.

3 数值算例

为了验证本文拓扑优化方法的可行性、可靠性和高效性，针对长960 mm、高320 mm 的悬臂梁和长960 mm、高480 mm Michell 结构的棋盘格现象、数值不稳定、灵敏度过滤慢等问题开展了数值实验，如图2 和3所示（算例优化参数为体积约束比为0.5、弹性模量为1 GPa、Poisson 比为0.3、惩罚因子为3、移动极限为0.2、外载荷F为1 kN）.拓扑优化程序基于文献[16,20]的MATLAB 代码进行编写，在PDE 滤波器的求解中引入了共轭梯度（CG）算法、多重网格（MG）算法以及多重网格预处理共轭梯度（MGCG）算法，并比较了三种算法对结构拓扑优化效率的影响，相关数值结果如下.

图2 悬臂梁Fig.2 The cantilever beam

图3 Michell 结构Fig.3 The Michell structure

3.1 精度的影响

依次取4 种不同的误差精度P(P=1E–2,1E–3,1E–4,1E–5)，采用CG 算法、网格层数为5 的MG 算法和MGCG 算法求解经有限元分析Helmholtz 方程得到的代数方程，并对整个结构分别划分为480×160和480×240个单元的悬臂梁和Michell 结构进行半径为6 的PDE 灵敏度过滤拓扑优化实验.其中，不同精度下悬臂梁和Michell 结构的优化结构、目标柔度值C、整体迭代次数I以及整体优化时间T的分布如图4、图5、表1、图6、图7所示.

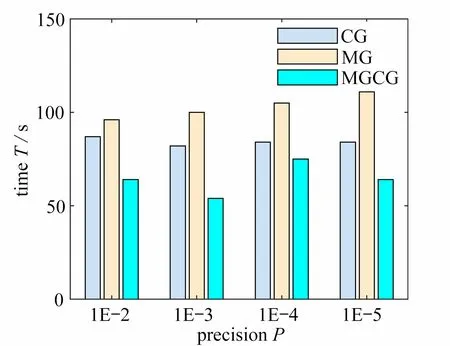
图6 悬臂梁结构优化时间分布图Fig.6 The optimized time distribution of the cantilever beam

图7 Michell 结构优化时间分布图Fig.7 The optimized time distribution of the Michell structure

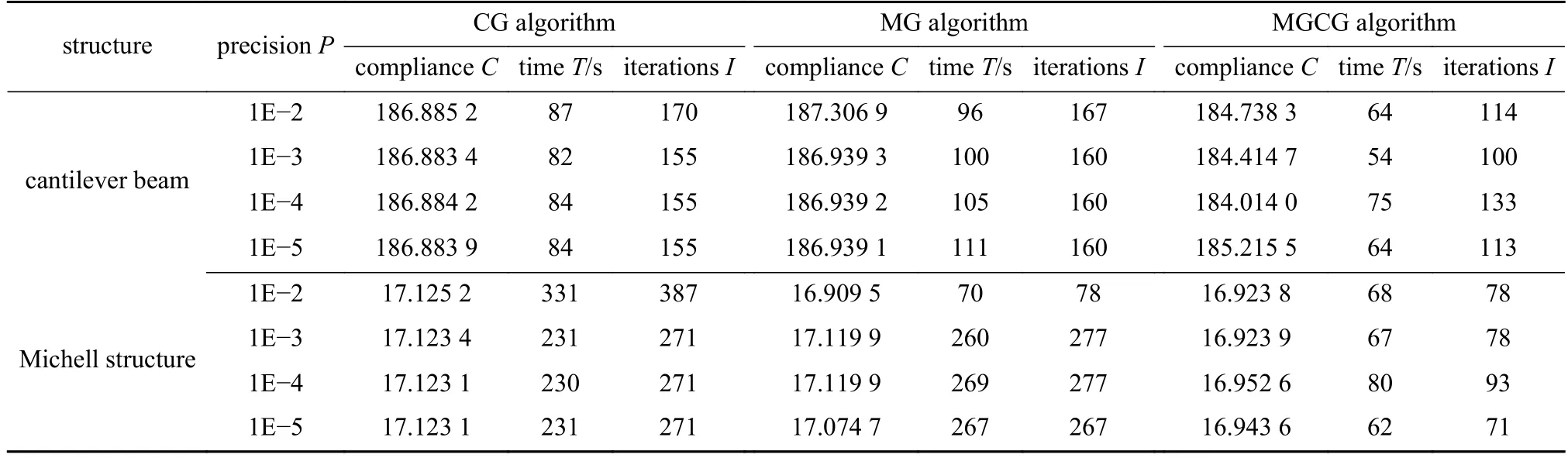
表1 两种结构的拓扑优化迭代次数和柔度值Table 1 Total numbers of iterations and compliance for topology optimization of 2 structures

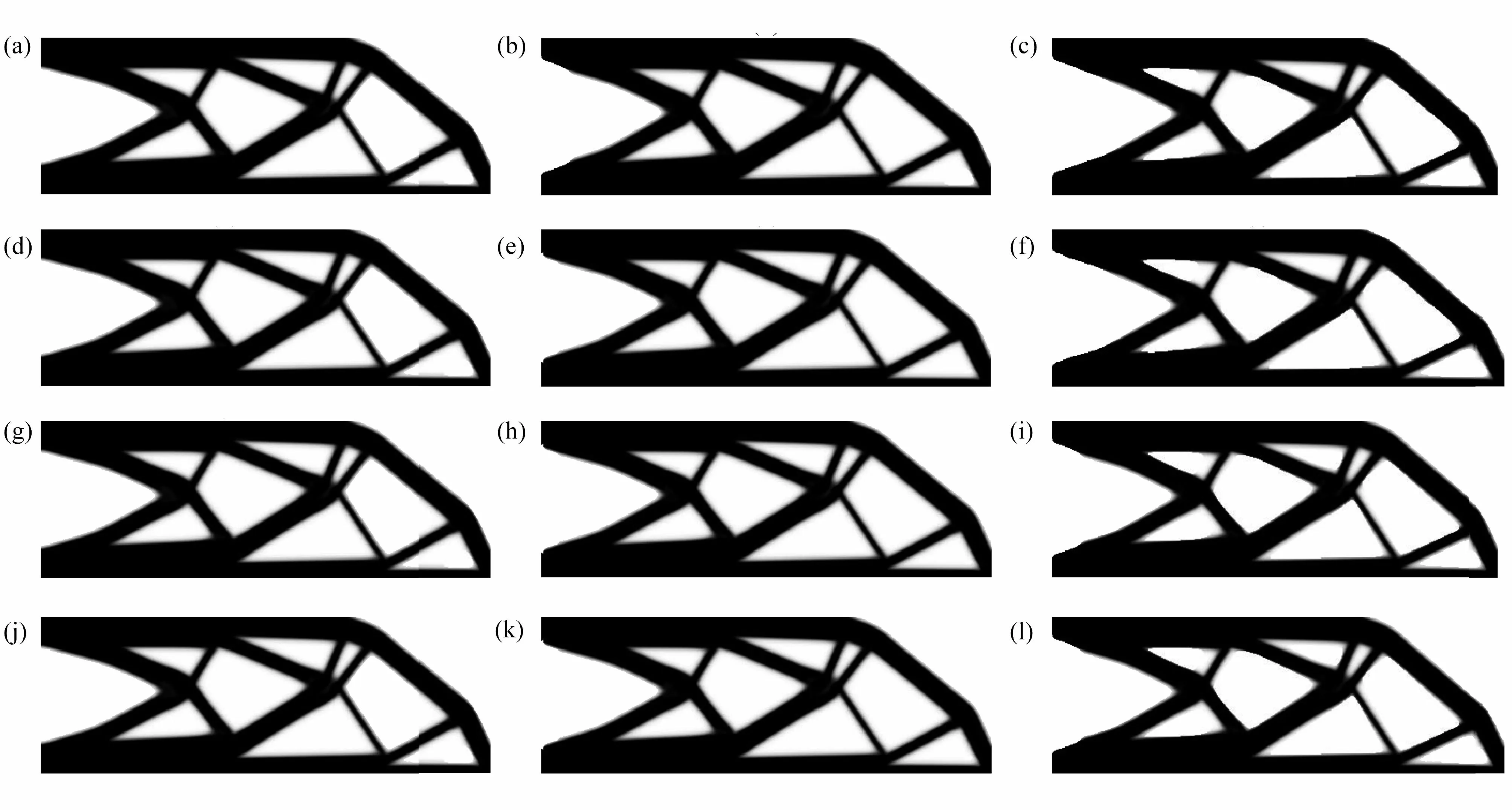
图4 不同精度下CG、MG 和MGCG 算法的悬臂梁的优化结构：(a)P=1E−2 (CG)；(b)P=1E−2 (MG)；(c)P=1E−2 (MGCG)；(d)P=1E−3 (CG)；(e)P=1E−3(MG)；(f)P=1E−3 (MGCG)；(g)P=1E−4 (CG)；(h)P=1E−4 (MG)；(i)P=1E−4 (MGCG)；(j)P=1E−5 (CG)；(k)P=1E−5 (MG)；(l)P=1E−5 (MGCG)Fig.4 The optimized cantilever beams by CG,MG and MGCG algorithms with different degrees of precision:(a)P=1E−2 (CG);(b)P=1E−2 (MG);(c)P=1E−2 (MGCG);(d)P=1E−3 (CG);(e)P=1E−3 (MG);(f)P=1E−3 (MGCG);(g)P=1E−4 (CG);(h)P=1E−4 (MG);(i)P=1E−4 (MGCG);(j)P=1E−5 (CG);(k)P=1E−5 (MG);(l)P=1E−5 (MGCG)

图5 不同精度下CG、MG 和MGCG 算法的Michell 结构的优化结构：(a)P=1E−2 (CG)；(b)P=1E−2 (MG)；(c)P=1E−2 (MGCG)；(d)P=1E−3 (CG)；(e)P=1E−3(MG)；(f)P=1E−3 (MGCG)；(g)P=1E−4 (CG)；(h)P=1E−4 (MG)；(i)P=1E−4 (MGCG)；(j)P=1E−5 (CG)；(k)P=1E−5 (MG)；(l)P=1E−5 (MGCG)Fig.5 The optimized Michell structures by CG,MG and MGCG algorithms with different degrees of precision:(a)P=1E−2 (CG);(b)P=1E−2 (MG);(c)P=1E−2 (MGCG);(d)P=1E−3 (CG);(e)P=1E−3 (MG);(f)P=1E−3 (MGCG);(g)P=1E−4 (CG);(h)P=1E−4 (MG);(i)P=1E−4 (MGCG);(j)P=1E−5 (CG);(k)P=1E−5 (MG);(l)P=1E−5 (MGCG)

从图4、图5 和表1 可以看出，在过滤半径为6 的PDE 灵敏度滤波器中使用不同精度的CG 算法、MG 算法和MGCG 算法得到的悬臂梁和Michell 结构的优化结构图基本相同，并且目标函数值非常接近，至多相差1%，说明PDE 滤波器求解算法的精度对拓扑优化的结果影响不大.此外，在PDE 滤波器中使用MGCG 算法进行结构拓扑优化的迭代次数整体低于其他两种算法.

从图6 和图7 可以看出，同一精度下，在PDE 滤波器中使用MGCG 算法进行结构拓扑优化的时间整体低于CG 算法和MGCG 算法，且随着精度的增加，在PDE 滤波器中使用CG 算法进行结构拓扑优化的时间逐渐降低并趋于稳定，在PDE 滤波器中使用MG 算法进行结构拓扑优化的时间逐渐增加并趋于稳定.此外，在PDE 滤波器中采用MGCG 算法对悬臂梁和Michell 结构拓扑优化的时间分别比CG 算法少了11% ～ 34%和65% ～ 80%，比MG 算法少了29% ～ 46%，3%和77%.因此，从结构的整体优化效率看，MGCG 算法高于CG 算法和MG 算法.

3.2 过滤半径的影响

依次取4 种不同的过滤半径R(R=3，6，9，12),采用CG 算法、网格层数为5 的MG 算法以及MGCG 算法求解有限元分析Helmholtz 方程得到的代数方程，并对整个结构分别划分为480×160和480×240个单元的悬臂梁和Michell 结构进行控制精度为1E–4 的PDE 灵敏度过滤的拓扑优化实验.其中，不同过滤半径下悬臂梁和Michell 结构的优化结构、目标柔度值C、整体迭代次数I以及整体优化时间T的分布分别如图8、图9、表2、图10、图11所示.

图8 不同过滤半径下CG、MG 和MGCG 算法的悬臂梁的优化结构：(a)R=3 (CG)；(b)R=3 (MG)；(c)R=3 (MGCG)；(d)R=6 (CG)；(e)R=6 (MG)；(f)R=6 (MGCG)；(g)R=9 (CG)；(h)R=9 (MG)；(i)R=9 (MGCG)；(j)R=12 (CG)；(k)R=12 (MG)；(l)R=12 (MGCG)Fig.8 The optimized cantilever beams by CG,MG and MGCG algorithms with different filter radius:(a)R=3 (CG);(b)R=3 (MG);(c)R=3 (MGCG);(d)R=6 (CG);(e)R=6 (MG);(f)R=6 (MGCG);(g)R=9 (CG);(h)R=9 (MG);(i)R=9 (MGCG);(j)R=12 (CG);(k)R=12 (MG);(l)R=12 (MGCG)

图9 不同过滤半径下CG、MG 和MGCG 算法的Michell 结构的优化结构：(a)R=3 (CG)；(b)R=3 (MG)；(c)R=3 (MGCG)；(d)R=6 (CG)；(e)R=6 (MG)；(f)R=6 (MGCG)；(g)R=9 (CG)；(h)R=9 (MG)；(i)R=9 (MGCG)；(j)R=12 (CG)；(k)R=12 (MG)；(l)R=12 (MGCG)Fig.9 The optimized Michell structures by CG,MG and MGCG algorithms with different filter radius:(a)R=3 (CG);(b)R=3 (MG);(c)R=3 (MGCG);(d)R=6 (CG);(e)R=6 (MG);(f)R=6 (MGCG);(g)R=9 (CG);(h)R=9 (MG);(i)R=9 (MGCG);(j)R=12 (CG);(k)R=12 (MG);(l)R=12 (MGCG)

图10 悬臂梁结构优化时间分布图(不同过滤半径)Fig.10 The optimized time distribution of the cantilever beam(different filter radius)

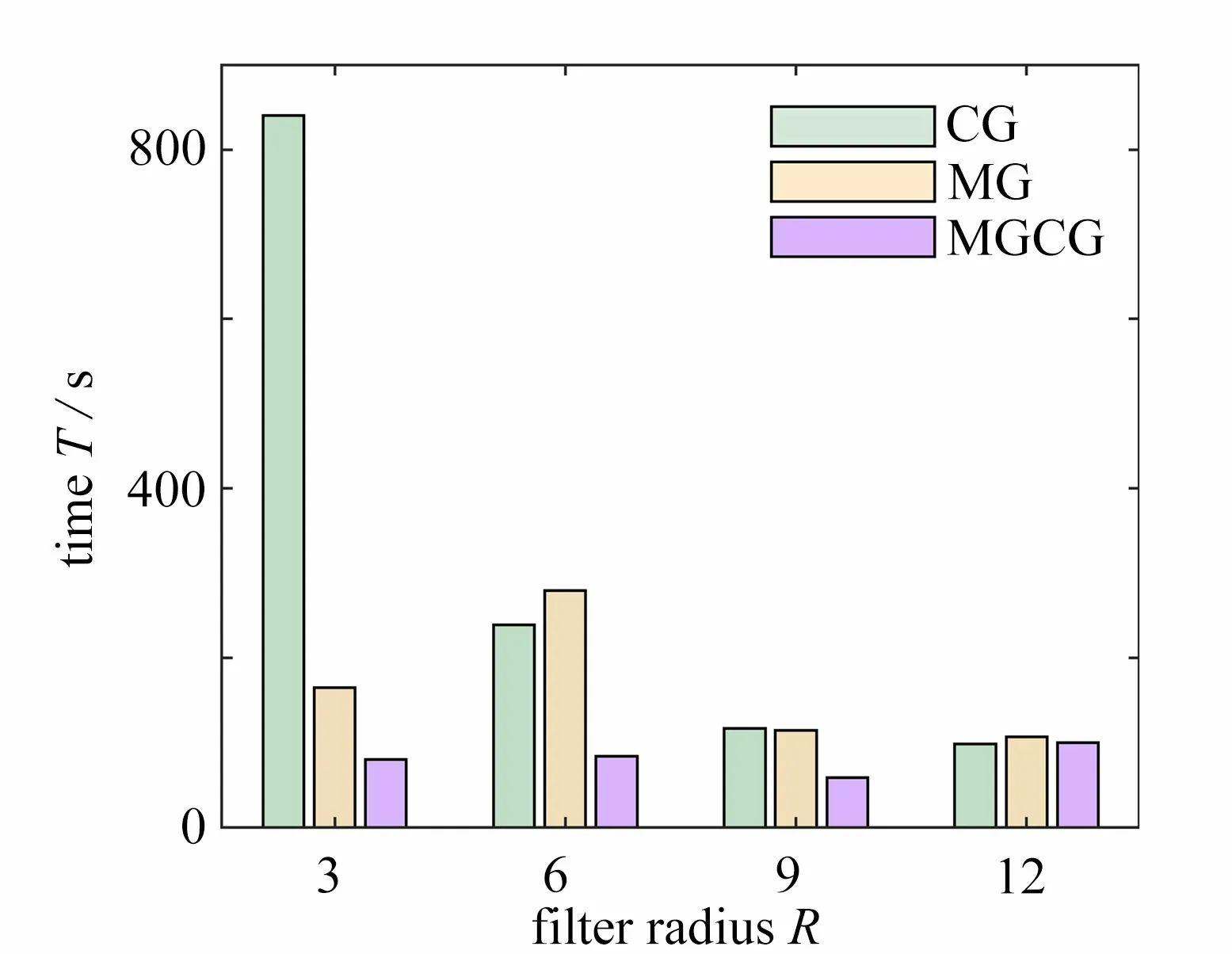
图11 Michell 结构优化时间分布图(不同过滤半径)Fig.11 The optimized time distribution of the Michell structure(different filter radius)

从图8、图9 和表2 可以看出，在PDE 灵敏度滤波器中使用精度为1E–4 的CG 算法、MG 算法和MGCG 算法得到的悬臂梁和Michell 结构的优化结构图、目标函数值的特征随着过滤半径的变化呈现类似的变化规律.随着过滤半径的增大，拓扑优化结构的清晰度越来越低，细支结构越来越少，说明该两种算法对结构承力路径的识别精度与过滤半径间体现出负相关性，且柔度值越来越大.且从表2 可以看出，随着过滤半径的改变，在PDE 滤波器中使用MG 算法和MGCG 算法进行结构拓扑优化的迭代次数整体低于CG 算法.

表2 两种结构的拓扑优化迭代次数和柔度值(不同过滤半径)Table 2 Total numbers of iterations and compliance for topology optimization of 2 structures (different filter radius)

从图10 和图11 可以看出，同一过滤半径下，在PDE 滤波器中使用MG 算法和MGCG 算法进行结构拓扑优化的时间整体低于CG 算法，且随着过滤半径增大，MGCG 算法的优势逐渐降低.此外，在PDE 滤波器中采用MGCG 算法对悬臂梁和Michell 结构拓扑优化的时间分别比CG 算法少了11%～89%和50%～91%，比MG 算法少了7%～61%，7%和70%.因此，从结构的整体优化效率看，MGCG 算法高于CG 算法和MG 算法.

3.3 网格数量的影响

分别对网格划分为960×320，过滤半径为12，层数为6；网格划分为480×160，过滤半径为6，层数为5；网格划分为240×80，过滤半径为3，层数为4 的悬臂梁和网格划分为960×480，过滤半径为12，层数为6；网格划分为480×240，过滤半径为6，层数为5；网格划分为240×120，过滤半径为3，层数为4 的Michell 结构进行控制精度为1E–4 的PDE 灵敏度过滤的拓扑优化实验.其中，不同网格数量下悬臂梁和Michell 结构的优化结构、目标柔度值C、整体迭代次数I以及整体优化时间T的分布分别如图12、图13、表3、图14、图15所示.

从图12、图13 和表3 可以看出，在PDE 灵敏度滤波器中使用精度为1E–4 的CG 算法、MG 算法和MGCG 算法得到不同网格数量的悬臂梁和Michell 结构的优化结构基本相同，并且随着网格数量增加，柔度值越来越大.可见PDE 滤波器求解算法对不同网格数量的优化结构影响不大，且可有效地消除网格依赖性和棋盘格现象.此外，在PDE 滤波器中使用MGCG 算法进行结构拓扑优化的迭代次数整体低于其他两种算法.

表3 两种结构的拓扑优化迭代次数和柔度值(不同网格数量)Table 3 Total numbers of iterations and compliance for topology optimization of 2 structures (different grids)

图12 不同网格数量下CG、MG 和MGCG 算法的悬臂梁的优化结构：(a)网格为240 × 80 (CG)；(b)网格为240 × 80 (MG)；(c)网格为240 × 80 (MGCG)；(d)网格为480 × 160 (CG)；(e)网格为480 × 160 (MG)；(f)网格为480 × 160 (MGCG)；(g)网格为960 × 320 (CG)；(h)网格为960 × 320 (MG)；(i)网格为960 × 320 (MGCG)Fig.12 The optimized cantilever beams by CG,MG and MGCG algorithms with different grids:(a)grid 240 × 80 (CG);(b)grid 240 × 80 (MG);(c)grid 240 × 80 (MGCG);(d)grid 480 × 160 (CG);(e)grid 480 × 160 (MG);(f)grid 480 × 160 (MGCG);(g)grid 960 × 320 (CG);(h)grid 960 × 320 (MG);(i)grid 960 × 320 (MGCG)

图13 不同网格数量下CG、MG 和MGCG 算法的Michell 结构的优化结构：(a)网格为240 × 120 (CG)；(b)网格为240 × 120 (MG)；(c)网格为240 × 120 (MGCG)；(d)网格为480 × 240 (CG)；(e)网格为480 × 240 (MG)；(f)网格为480 × 240 (MGCG)；(g)网格为960 × 480 (CG)；(h)网格为960 × 480 (MG)；(i)网格为960 × 480 (MGCG)Fig.13 The optimized Michell structures by CG,MG and MGCG algorithms with different grids:(a)grid 240 × 120 (CG);(b)grid 240 × 120 (MG);(c)grid 240 × 120 (MGCG);(d)grid 480 × 240 (CG);(e)grid 480 × 240 (MG);(f)grid 480 × 240 (MGCG);(g)grid 960 × 480 (CG);(h)grid 960 × 480 (MG);(i)grid 960 × 480 (MGCG)

从图14 和图15 可以看出，同一网格数量下，在PDE 滤波器中使用MGCG 算法进行结构拓扑优化的时间整体低于CG 算法和MGCG 算法.特别地，在PDE 滤波器中采用MGCG 算法对悬臂梁和Michell 结构拓扑优化的时间分别比CG 算法少了3% ～ 25%和64% ～ 73%，比MG 算法少了15% ～ 37%，25%和76%.因此，从结构的整体优化效率看，MGCG 算法高于CG 算法和MG 算法.

图14 悬臂梁结构优化时间分布图(不同网格数量)Fig.14 The optimized time distribution of the cantilever beam(different grids)

图15 Michell 结构优化时间分布图(不同网格数量)Fig.15 The optimized time distribution of the Michell structure(different grids)

4 结论

本文在PDE 灵敏度滤波器中引入了CG 算法、MG 算法和MGCG 算法，对悬臂梁和Michell 结构进行拓扑优化，并比较了算法精度、过滤半径和网格数量对优化结果和优化效率的影响.实验结果表明：

1）不同精度的三种算法得到的优化结构、目标函数值基本相同.随着精度的提升，MG 算法的结构优化时间不断增加，CG 算法总体趋于稳定，MGCG 算法有微小的波动，且MGCG 算法结构优化时间整体少于其他两种算法.

2）随着过滤半径的增大，CG 算法和MG 算法的结构优化时间大幅减少，整体呈下降趋势，MGCG 算法有微小的波动，但优化时间整体少于其他两种算法，且过滤半径越小，优势越明显.

3）不同网格数量的三种算法得到的优化结构、目标函数值基本相同.随着网格数量的增加，三种算法的结构优化时间和迭代次数整体呈上升趋势，且随着网格数量的增加，MGCG 算法的优势越明显.

因此，从结构的整体优化效率看，MGCG 算法优于CG 算法和MG 算法.