多孔结构多尺度随机振动分析的渐近均匀化-时域显式法*

苏 成，罗俊哲，许 秩

（1.华南理工大学 土木与交通学院，广州 510640；2.华南理工大学 亚热带建筑科学国家重点实验室，广州 510640；3.人工智能与数字经济广东省实验室，广州 510330）

引言

多孔结构是由含一定数量相互贯通或封闭孔洞的固体材料组成的结构[1].由于具有高比强、高比刚度等优点，多孔结构在土木工程、机械工程和航天航空工程等领域得到了广泛应用[2-6].由于周期性多孔结构更易制备，因而在工程中的应用更为广泛.在工程应用中，多孔结构通常承受随机动力荷载的作用，其随机振动及动力可靠度分析对保障结构安全具有重要的意义.

由于多孔结构具有非均质特性，因此采用单一尺度有限元法进行结构分析时，需要采用非常精细的有限元网格，导致计算量十分巨大.多尺度分析方法[7-8]通过建立不同尺度的模型，把单一尺度下的复杂问题分解为不同尺度下的简单问题，可在保证计算精度的前提下大幅提高整体计算效率，是解决多孔结构计算问题的一类重要方法.在多尺度分析方法中，渐近均匀化法[9-11]是一种具有严格数学基础的方法，当引入的特征参数ε趋近于0 时，该方法的计算结果收敛于精确解答.

在随机动力荷载作用下多孔结构随机振动问题的研究尚不多见.文献[12]采用功率谱法研究了理想白噪声平稳随机荷载作用下多孔弹性板的随机振动问题.然而，对于非平稳随机振动问题，为了获得结构响应的演化功率谱，功率谱法需要在大量的离散频率点上进行时域积分运算，难以应用于实际工程中的多孔结构问题.近年来提出的一类非平稳随机振动时域显式法[13-16]，通过构建结构动力响应的时域显式表达式，能够在时域内直接建立非平稳响应统计矩的显式列式，实现任意自由度上的降维计算，已成功应用于非均质结构非平稳随机响应问题[17].

本文综合多尺度渐近均匀化法和随机振动时域显式法的计算优势，实现了非平稳随机激励下多孔结构随机振动问题的高效求解.首先采用多尺度渐近均匀化法推导并求解了多孔结构动力问题的多尺度控制微分方程，建立了多孔结构宏观和细观动力响应的时域显式表达式；然后结合结构随机振动时域显式法，获得了非平稳随机激励下多孔结构动力响应统计矩的演化规律.数值算例表明，本文所提出的方法具有理想的计算精度与计算效率.

1 多尺度动力分析的渐近均匀化法

1.1 多尺度动力学模型

周期性多孔结构由周期性分布的带孔单胞组成，如图1所示.单胞的尺度比整个结构的尺度小得多，即w×h≪W×H.设两者的比为ε量级，0<ε ≪1，ε称为特征参数.在多尺度渐近均匀化分析方法中，需要用到宏观坐标(x,y)和细观坐标(ξ,η)，这两组坐标满足以下关系式：

图1 周期性多孔结构和宏观等效结构Fig.1 The periodic porous structure and the macroscopic equivalent structure

假设场函数Φ(x,y)表示单一尺度坐标下多孔结构的材料场（如弹性模量、Poisson 比等）、荷载场（如体力）和结构响应场（如位移、应力和应变等）.对于周期性多孔结构，场函数Φ(x,y)原则上应包含周期性部分.将周期性部分改用细观坐标(ξ,η)表达，从而得到扩充坐标后的多尺度坐标下多孔结构的场函数Φε(x,y,ξ,η)，它是关于细观坐标(ξ,η)的周期函数，周期为单胞尺寸.显然，Φ(x,y)和 Φε(x,y,ξ,η)满足以下关系：

式中k1和k2为整数，w和h为单胞尺寸.

相应地，Φ(x,y)的偏导数可以用Φε(x,y,ξ,η)的偏导数表示为

在单一尺度坐标下，多孔结构的控制微分方程可表示为

式中

按式(2)和式(3)的方式扩充坐标后，多尺度坐标下的多孔结构控制微分方程可表示为

式中

其中带ε的函数分别为式(5)中各函数扩充坐标后得到的多尺度坐标下的函数；∂ε为关于(ξ,η)的微分算子矩阵.值得注意的是，由于周期性多孔结构的材料属性呈周期性变化，因此ρε(ξ,η)，cε(ξ,η)，Eε(ξ,η)和νε(ξ,η)与宏观坐标(x,y)无关.

对多尺度坐标下的位移向量进行关于特征参数ε的多尺度渐近展开，并保留前三项得[18]

式中u(0)，u(1)和u(2)分别为由位移的零阶、一阶和二阶展开函数组成的向量.

将式(8)代入式(6)，整理后得到多尺度坐标下多孔结构控制微分方程关于特征参数ε的展开形式为

保留前三项并考虑到ε的任意性，上式成立的必要条件是

在式(8)中通常采用u(0)来反映位移随宏观坐标(x,y)的变化，u(0)称为宏观位移向量.显然，u(0)与细观坐标(ξ,η)无关，即u(0)=u(0)(x,y)，因此式(10)自动成立.由式(11)和式(12)可以分别导出单胞控制微分方程和宏观控制微分方程.

1.2 单胞控制微分方程

对u(1)进行分离变量，将它表示为以下乘积形式：

式中X=X(ξ,η)，称为单胞特征位移矩阵，其只与单胞内细观坐标(ξ,η)有关，表示为

将式(13)代入式(11)，可得

由于∂u(0)不恒等于0，所以上式成立的必要条件为

式(16)只与细观坐标(ξ,η)相关，用于求解单胞特征位移矩阵，称为单胞控制微分方程.该方程也可以表达为如下形式：

式中Xi表示X的第i列；ei表示为

显然，式(17)可以理解为在不同方向单位初应变ei作用下的单胞静力平衡微分方程，解之即可获得Xi(i=1,2,3)，从而按式(14)构造单胞特征位移矩阵X.值得注意的是，对于周期性多孔结构，在求解式(17)时，只需要考虑一个典型单胞区域.对于图1所示的具有双对称轴的单胞区域，考虑到周期性边界条件的要求，在单位初应变e1或e2作用下，需对单胞外围边界施以法向固定的边界条件；在单位初应变e3作用下，需对单胞外围边界施以切向固定的边界条件[19].

显然，式(17)可以理解为在不同方向单位初应变ei作用下的单胞静力平衡微分方程，解之即可获得Xi(i=1,2,3)，从而按式(14)构造单胞特征位移矩阵X.值得注意的是，对于周期性多孔结构，在求解式(17)时，只需要考虑一个典型单胞区域.对于图1所示的具有双对称轴的单胞区域，考虑到周期性边界条件的要求，在单位初应变e1或e2作用下，需对单胞外围边界施以法向固定的边界条件；在单位初应变e3作用下，需对单胞外围边界施以切向固定的边界条件[19].

根据单胞特征位移矩阵和本构方程进一步定义单胞特征应力矩阵为

该矩阵可用于计算下文的宏观弹性矩阵.

1.3 宏观控制微分方程

将式(13)代入式(12)，并考虑式(19)得

根据Fredholm 定理[20]，关于u(2)的椭圆型偏微分方程有且仅有唯一解的必要条件为方程的非齐次项在单胞内积分为0，即

式中V为单胞的面积.

文献[21]证明了以下等式：

将式(22)代入式(21)中，可得宏观控制微分方程：

式中

显然，式(23)可以理解为关于宏观位移向量u(0)的宏观运动微分方程，式中 ρH，cH，DH和fH分别为宏观质量密度矩阵、宏观阻尼系数矩阵、宏观弹性矩阵和宏观体力向量.该方程的求解区域为图1所示的宏观等效结构区域，其边界条件与实际问题一致.式(24)～(27)称为均匀化方程，用于求解各均匀化宏观参数，其中宏观弹 性矩阵DH依赖于1.2 小节获得的单胞特征应力矩阵 Υ.

1.4 回代分析

将式(13)代入式(8)，并略去 ε2项，可得单胞细观位移向量uε的表达式为

式中单胞特征位移矩阵X可由单胞静力平衡微分方程式(17)求得，而宏观位移向量u(0)则由宏观运动微分方程式(23)求得.

单胞细观应力向量 σε可根据几何方程和本构方程由uε求得，表达式为

将式(28)代入式(29)并略去 ε1项，可得

式中单胞特征应力矩阵 Υ见式(19).

2 多尺度随机振动分析的时域显式法

2.1 宏观动力响应时域显式表达式

首先进行单胞分析.采用静力有限元法求解式(17)所示的单胞静力平衡微分方程，此时需要将图1所示的单胞划分为细观有限元网格，由此求得单胞内各细观单元节点的特征位移矩阵和特征应力矩阵，进一步由式(26)获得式(23)所需的宏观弹性矩阵.

然后进行宏观分析.采用动力有限元法求解式(23)所示的宏观运动微分方程，此时需要将图1所示的宏观等效结构划分为宏观有限元网格（宏观单元的尺寸一般取为单胞尺寸），从而式(23)可以离散为以下形式：

式中M，C和K分别为宏观质量、阻尼和刚度矩阵；分别为宏观节点位移、速度和加速度向量；F为非平稳随机激励向量，L为其定位矩阵.

记时间步长为 ∆t，积分步数为n，把随机激励向量F离散为时刻0,t1,t2,···,tn处的荷载向量F0,F1,F2,···,Fn.假定结构响应具有零初值，采用Newmark-β数值积分格式求解式(31)，可以推导得到宏观状态向量的显式表达式为

式中

其中

γ=0.5,β=0.25.

根据式(33)所揭示的系数矩阵之间的内在关系，可以把各系数矩阵排列如表1所示.由表1 可见，仅第一列系数矩阵Ai,0和第二列系数矩阵Ai,1(i=1,2,···,n)需要计算和存储，其计算量相当于对宏观等效结构进行2m次脉冲响应分析的计算量，m为荷载向量F的分量个数[22].

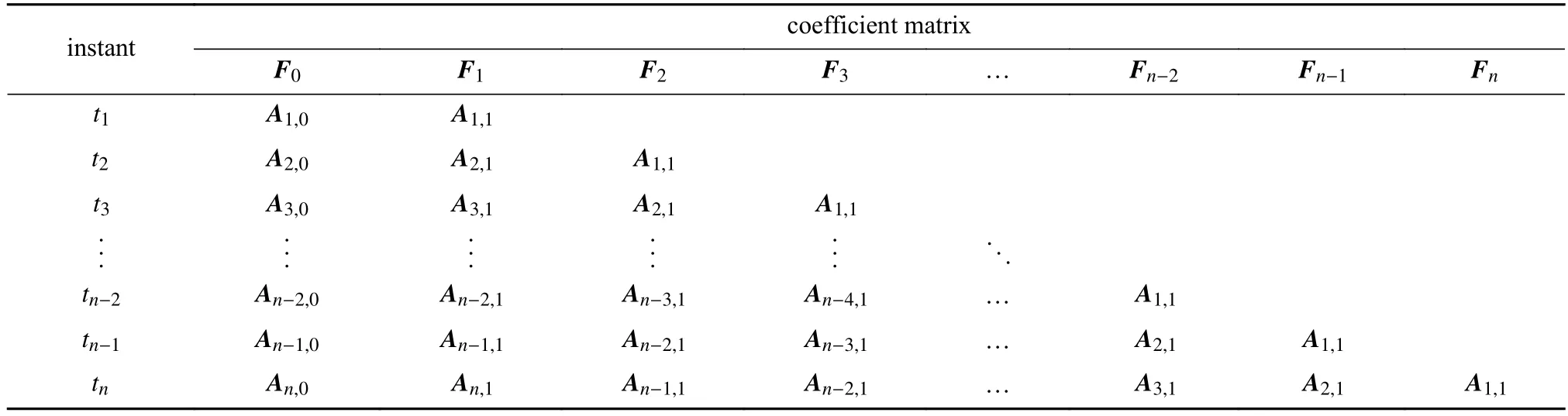
表1 各时刻显式表达式的系数矩阵Table 1 Coefficient matrices for explicit formulation at different instants

2.2 细观动力响应时域显式表达式

为了进一步建立单胞细观动力响应时域显式表达式，需要采用式(28)和式(30)进行回代分析.由该两式可以得到单胞细观单元节点位移向量及应力向量与宏观节点状态向量之间的关系：

将式(32)代入式(35)得

式中Ai,j的表达式见式(33).

在多孔结构的随机振动分析中，通常只需关注结构的某些关键响应.假设r为所关注的关键响应，如位移、应力等，则由式(36)可直接得到ri=r(ti)的显式表达式为

2.3 动力响应统计矩

前述工作利用多尺度渐近均匀化法建立了多孔结构动力响应的显式表达式，揭示了多孔结构的物理演化规律.在此基础上，可以进一步研究动力响应统计矩的演化规律.根据一阶矩和二阶矩的运算规则，由式(38)可得各时刻关键响应ri的均值和方差如下：

式中E(F[i])为F[i]的均值向量，cov(F[i],F[i])为F[i]的协方差矩阵，分别表示为

式 中µF(t)和RFF(t,τ)分别为非平稳随机激励向量F(t)的均值函数向量和互相关函数矩阵，i=1,2,···,n.

3 数值算例

如图1所示，底部固支的周期性多孔有机玻璃方形板边长和厚度分别为W=H=100 mm 和t=1 mm，单胞边长为w=h=10 mm，单胞中心有一边长为a=b=5 mm 的方孔.有机玻璃方形板[23]的弹性模量E=5.3 GPa，Poisson 比µ=0.3，密度ρ = 1.18 × 10−6kg/mm3.选取Rayleigh 阻尼模型，阻尼比取为ξ= 0.002.

该周期性多孔有机玻璃方形板在上部受到零均值非平稳随机激励f(t)的作用，f(t)取为均匀调制非平稳随机过程，即

式中g(t)为调制函数，用于反映随机过程的非平稳特性，取为

q(t)为零均值平稳随机过程，其相关函数取为

式中τ为时间间隔，λ=144 MPa2.于是，f(t)的相关函数可以表达为

根据式(45)所示的相关函数，可以采用Cholesky 分解法生成随机激励f(t)的样本，其中一个样本如图2所示.

图2 随机激励f(t)的一个样本Fig.2 A sample of random excitation f(t)

分别采用基于渐近均匀化法的多尺度有限元法以及单一尺度有限元法建立多孔结构动力响应时域显式表达式.在多尺度有限元法中，首先将图1所示的单胞划分为300 个四节点单元，通过单胞分析获得多孔材料宏观弹性模量和宏观Poisson 比分别为EH= 2.864 GPa 和µH= 0.1967；然后将整个宏观等效方形板划分为100 个四节点单元，并进行宏观分析.在单一尺度有限元法中，将整个多孔方形板划分为30000 个四节点单元，每个单元的尺寸与多尺度有限元法中单胞分析的细观单元尺寸一致.此外，在建立动力响应时域显式表达式时，所考虑的持时为T= 1 ms，时间步长取为 ∆t= 0.002 ms.

分别采用多尺度时域显式法和单一尺度时域显式法，考察图1所示单胞右侧孔边中点A的位移和应力.在图2所示荷载样本作用下，点A的位移时程uxA,uyA和应力时程 σyA分别如图3～5所示.此外，在式(42)所示的非平稳随机激励作用下，点A的位移方差时程D(uxA),D(uyA)和应力方差时程D(σyA)分别如图6～8所示.由图3～8 可见，两种方法的计算结果相当吻合，验证了多尺度时域显式法的正确性.

图3 点A 水平位移时程Fig.3 Time histories of the horizontal displacement at point A

图4 点A 竖向位移时程Fig.4 Time histories of the vertical displacement at point A

图5 点A 竖向正应力时程Fig.5 Time histories of the vertical normal stress at point A

图6 点A 水平位移方差时程Fig.6 Time histories of variance of the horizontal displacement at point A

图7 点A 竖向位移方差时程Fig.7 Time histories of variance of the vertical displacement at point A

图8 点A 竖向正应力方差时程Fig.8 Time histories of variance of the vertical normal stress at point A

在计算效率方面，多尺度时域显式法和单一尺度时域显式法的计算时间分别列于表2 中.计算在 Intel core i5 处理器和 8 GB 内存的台式计算机上完成.由表2 可见，两种方法的计算时间由两部分组成，分别用于构建动力响应时域显式表达式和统计矩运算.两种方法在统计矩运算方面的计算时间是一样的，主要区别在于动力响应显式表达式系数矩阵的计算时间.由于采用了多尺度渐近均匀化法，多尺度时域显式法用于构建动力响应显式表达式的计算时间仅为单一尺度方法的0.94%，从而显著提高了多孔结构非平稳随机振动问题的计算效率.

表2 两种方法的计算时间（单位：s）Table 2 Time costs of the 2 methods (unit:s)

4 结论

为了正确反映多孔材料细观非均质特性及动力荷载随机性的影响，本文开展了多孔结构随机振动分析的渐近均匀化-时域显式法研究，得到了以下结论：

1)所推导的周期性多孔结构动力问题多尺度控制微分方程充分体现了多尺度渐近均匀化思想，具有严格的数学基础，为多孔结构多尺度动力响应分析奠定了理论基础.

2)采用多尺度有限元法建立的多孔结构多尺度动力响应显式表达式，完全揭示了多孔结构的物理演化过程.在此基础上，通过多孔结构物理演化机制和概率演化机制的相对分离，实现了多孔结构细观动力响应演变统计矩的高效计算.

3)所提出的渐近均匀化-时域显式法综合发挥了多尺度渐近均匀化法和随机振动时域显式法的计算优势，大幅提升了多孔结构非平稳随机振动分析的计算精度和计算效率，为多孔结构随机振动问题提供了一条可行的途径.

值得指出的是，本文的方法并不局限于周期性多孔结构的分析，亦可用于一般周期性非均质材料的随机振动问题.在本文工作基础上，可以进一步研究非均质材料微结构随机振动灵敏度及随机拓扑优化问题.