不同梯度变化方式的不规则多孔结构设计与力学性能分析
汤永锋 路 平 刘 斌 江开勇 颜丙功 刘嘉伟 韩 伟
1.华侨大学福建省特种能场制造重点实验室,厦门,361021
2.华侨大学厦门市数字化视觉测量重点实验室,厦门,361021
0 引言
多孔结构因具有结构轻量化、比强度高、吸能减振、生物相容性好等优秀的性能,在航天航空、汽车、骨植入体等领域有着广泛的应用[1-5]。均匀的多孔结构力学性能单一,无法满足复杂多样的力学和生物性能要求,相比而言,梯度多孔结构通过调节孔隙率改变结构局部的力学性能,能够满足复杂多变的设计要求,如在骨组织工程中,梯度多孔结构能够更好地模拟低孔隙率的皮质骨到高孔隙的松质骨梯度变化[6-7]。
多孔结构从形态上可以分为规则多孔结构和不规则多孔结构,规则多孔结构主要通过单元阵列获得,建模简单,力学性能可控。例如,Van GRUNSVEN等[8]通过电子束熔融(electron beam melting,EBM)技术制备Ti6Al4V梯度钻石晶格,并利用混合原则预测了梯度多孔结构的压缩性能。ZHANG等[9]采用试验和有限元方法研究了梯度多孔结构在纵向上的压缩变形行为。规则多孔结构因受限于单元阵列建模方式,在形成梯度多孔结构时会存在明显的结构分层现象,这会对结构的制造和力学性能产生不利影响。不规则多孔结构不受单元结构限制,设计自由高,可以通过改变杆径或调整密度的方式生成平滑过渡的梯度多孔结构。目前,基于Voronoi图构建的梯度不规则多孔结构由于与自然界的多孔结构相似而受到大家的关注,如人体骨和天然海绵。GMEZ等[10]通过提取人体骨的CT图像结合Voronoi图原理来重建精确匹配人体骨小梁的多孔结构。WANG等[11]基于Voronoi图原理设计梯度多孔结构,通过激光选区熔化(selective laser melting,SLM)技术制备实验模型并进行压缩实验,研究了其力学性能和变形特点。LIU等[12]基于Voronoi图设计出目标驱动的几何和力学性能连续的梯度多孔结构。然而,目前对梯度多孔结构力学性能的研究主要集中于规则多孔结构,梯度变化方式简单,对不同变化方式的梯度不规则多孔结构的力学性能研究仍较少。
本文首先利用Rhino软件自带的参数化设计插件Grasshopper提出了一种基于Voronoi图的梯度不规则多孔结构设计方法,并设计了4种不同梯度变化方式的多孔结构;然后通过横向压缩和纵向压缩实验,研究不同梯度变化方式对多孔结构力学性能和变形行为的影响;最后引入等应力复合模型[13]和Voigt模型[14-15]结合Gibson-Ashby模型[1]预测梯度多孔结构的弹性模量。
1 材料和方法
1.1 均匀不规则多孔结构建模
本文的不规则多孔结构建模方法基于Voronoi图[16]原理。Voronoi图是以特定区域内的不同点作为种子点,通过相邻种子点连线的垂直平分线对空间进行划分。其定义如下:
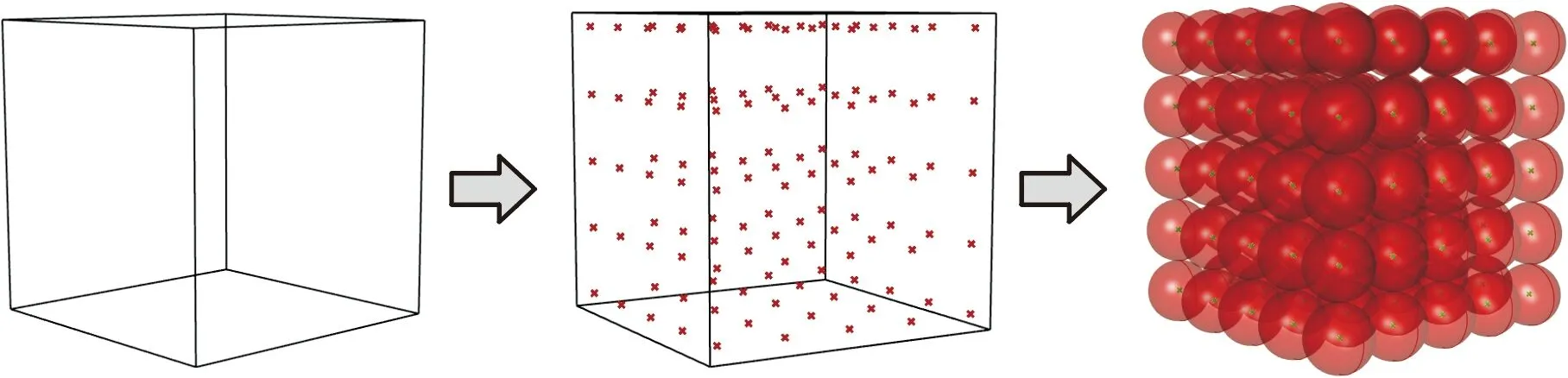
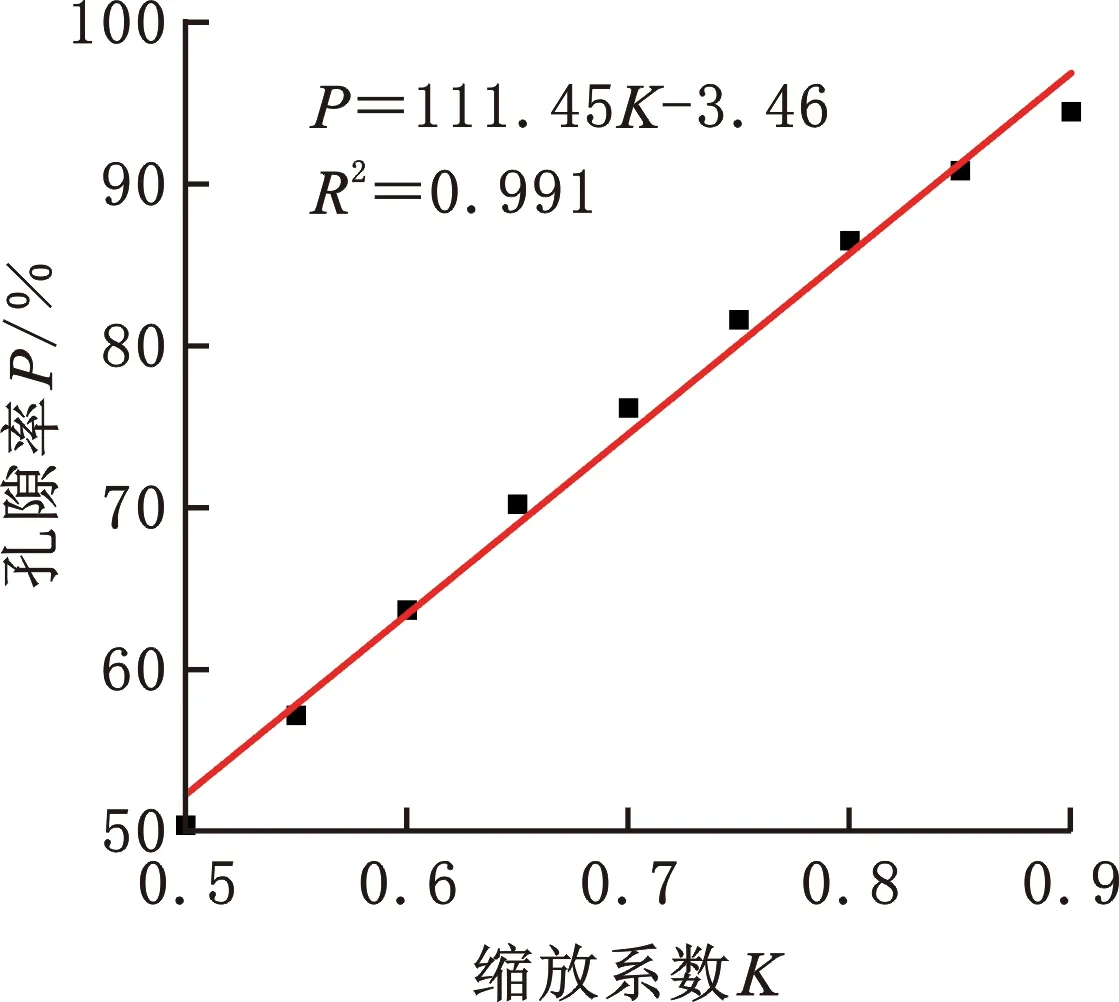
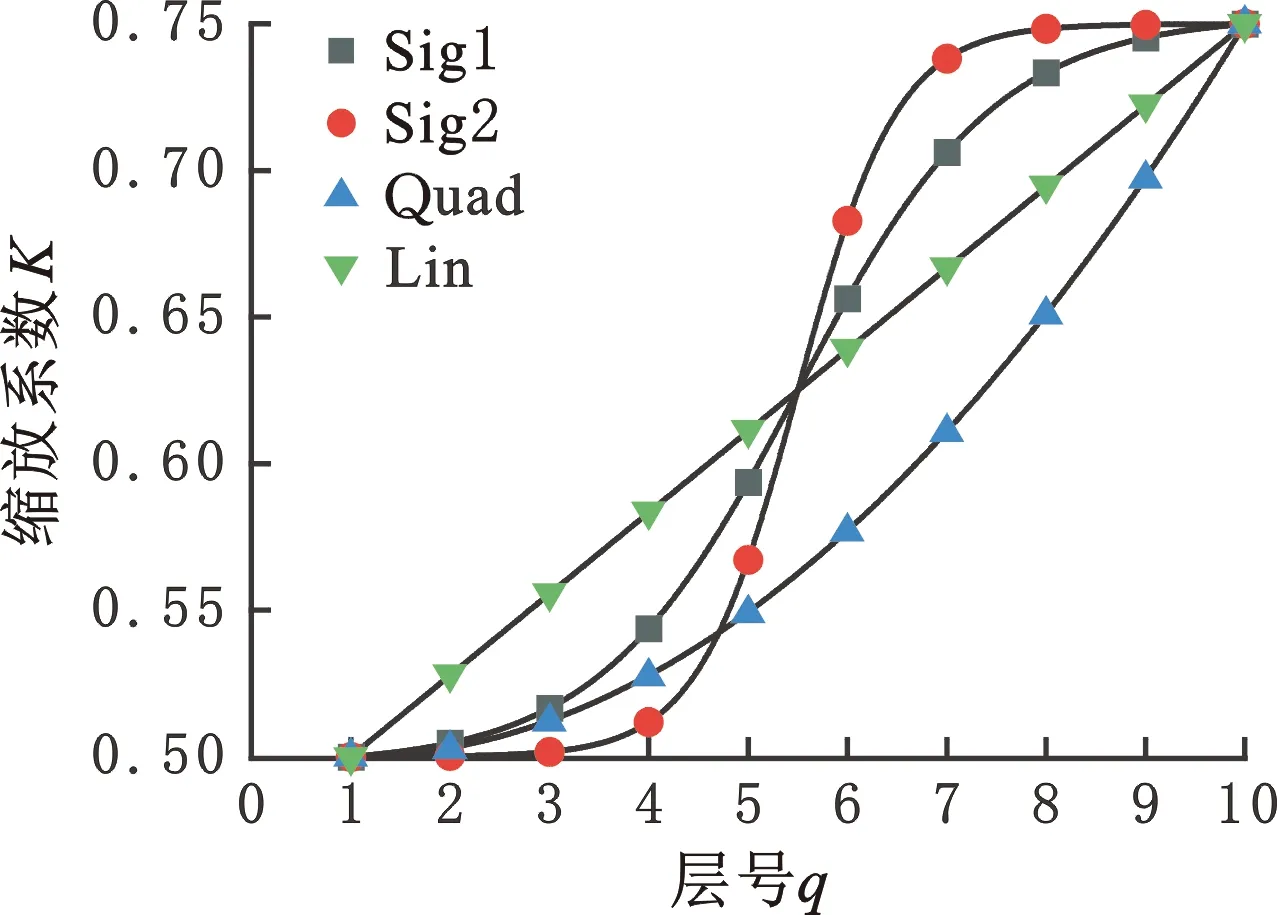
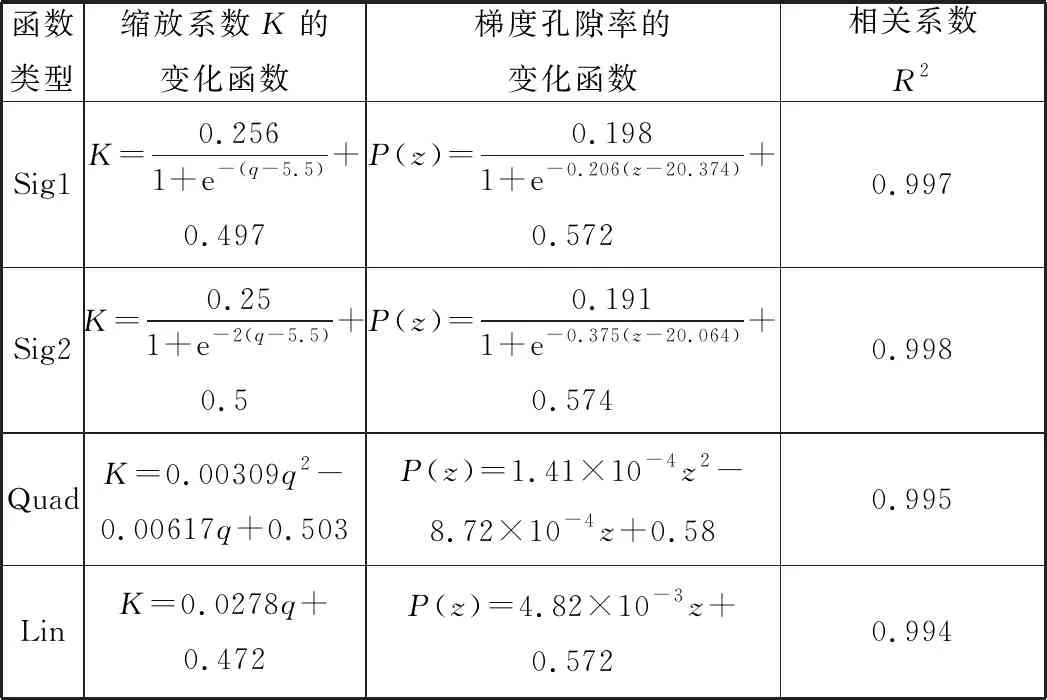
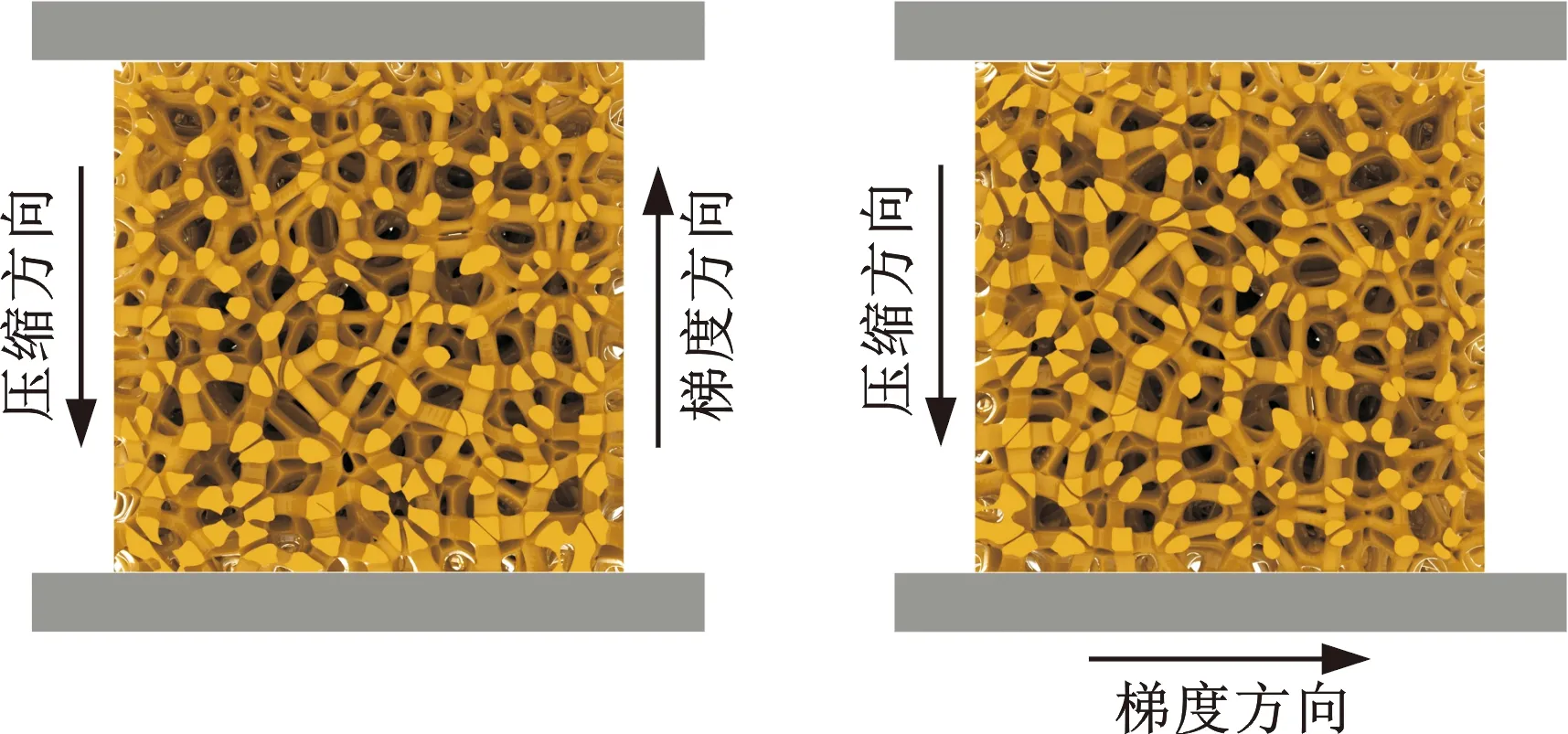
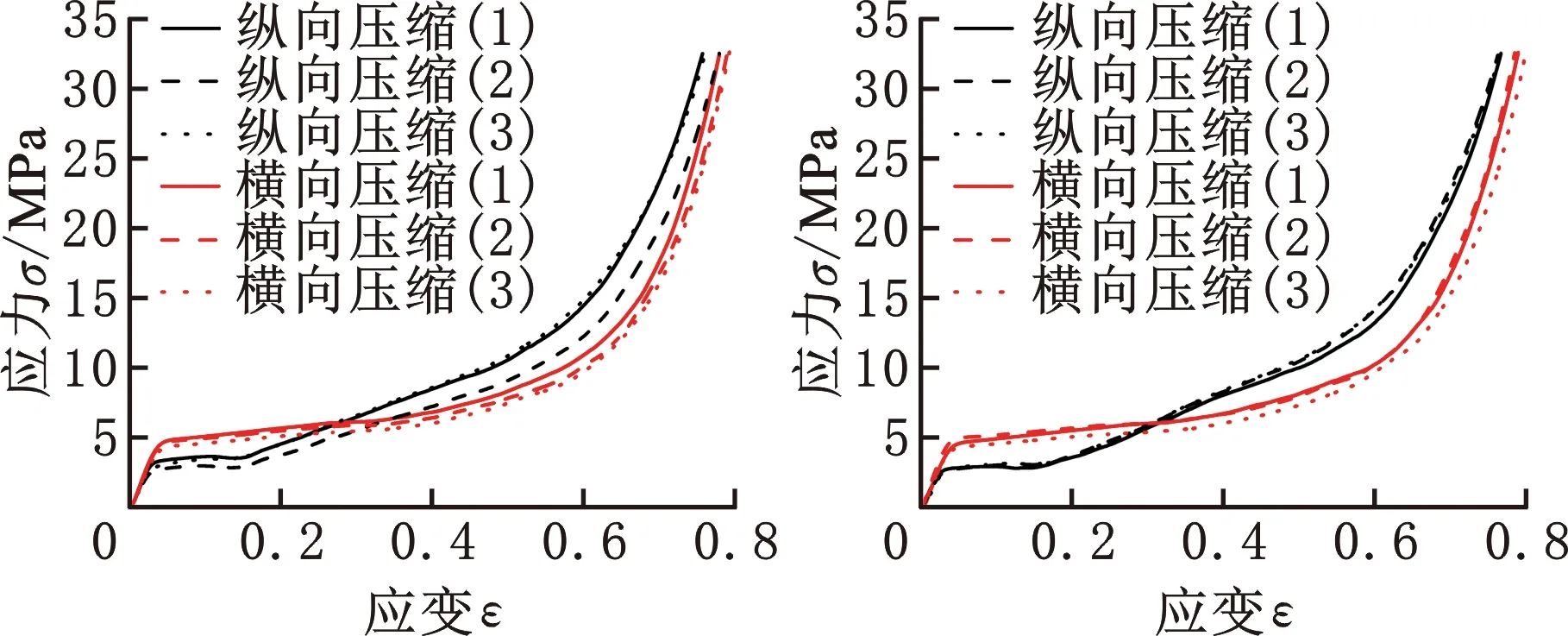
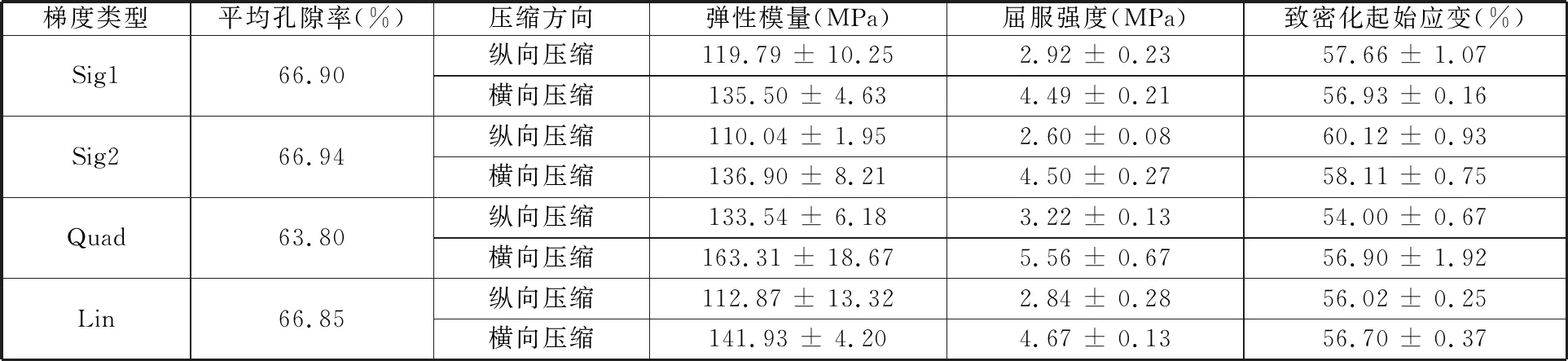
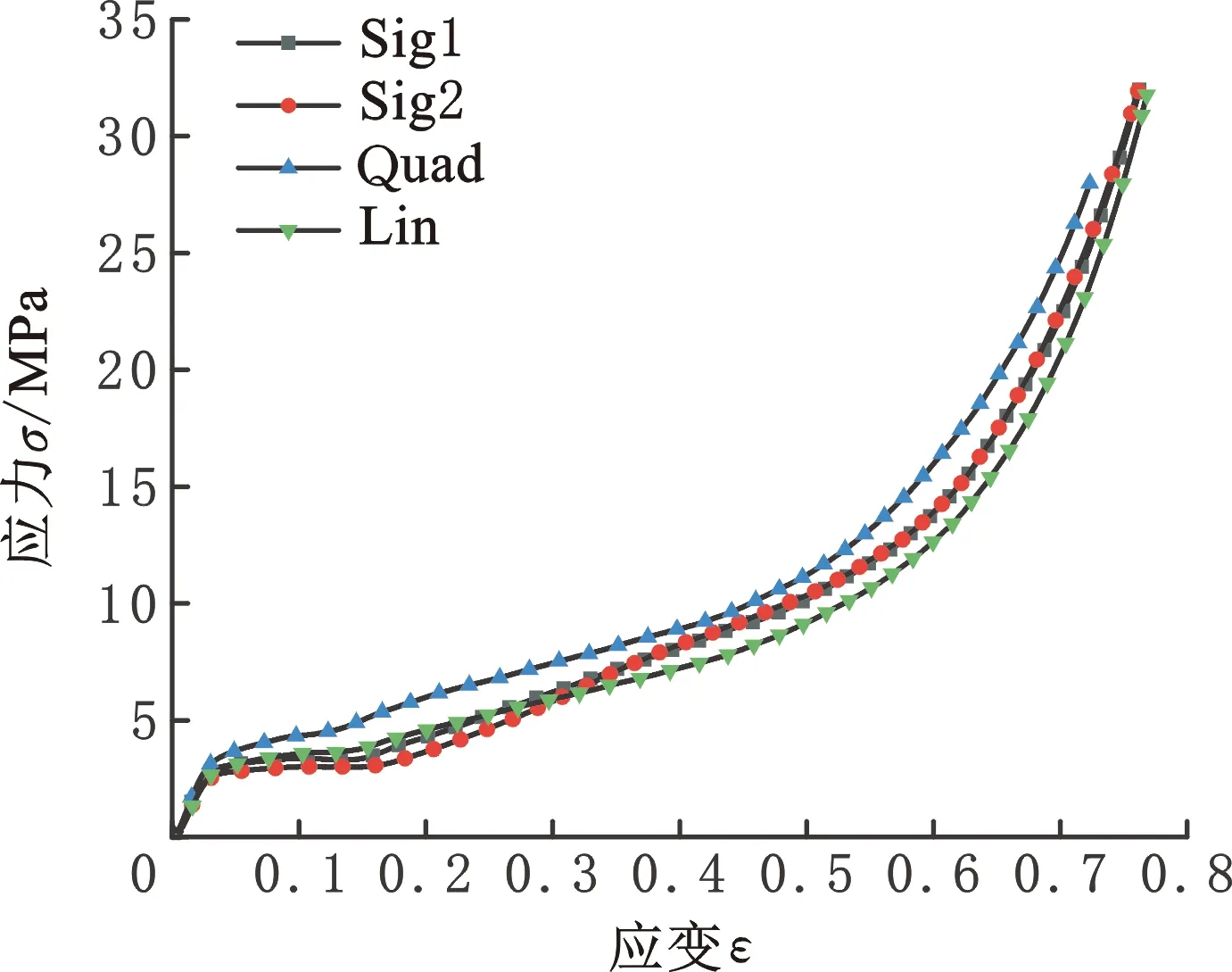
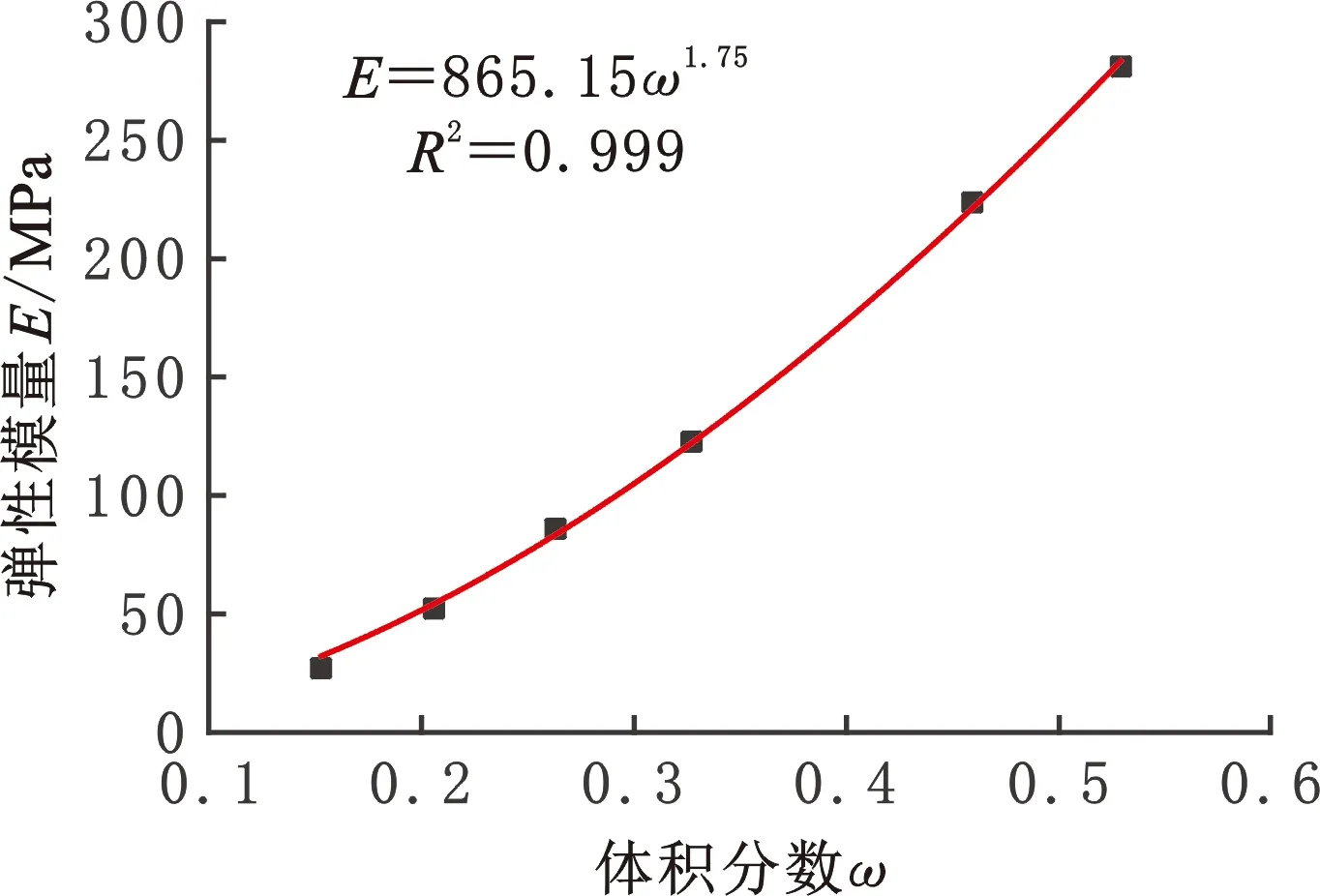
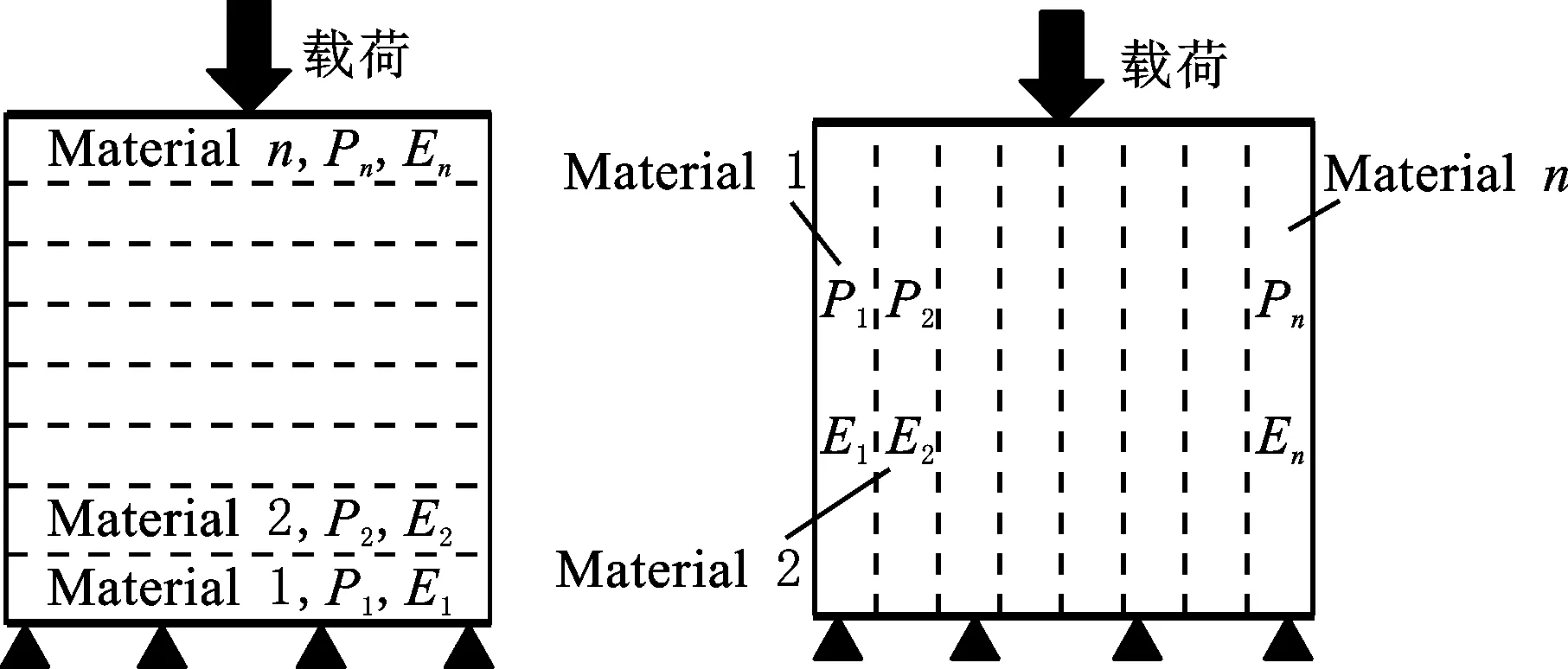
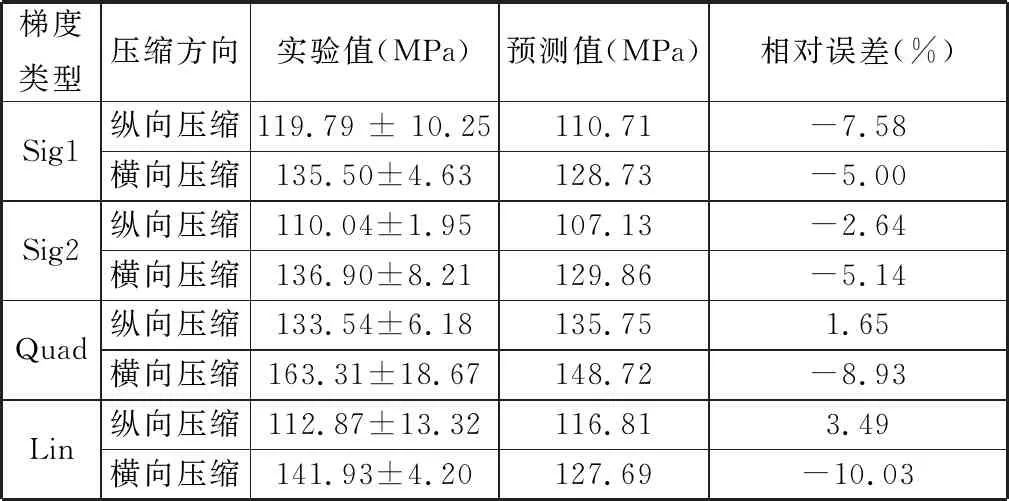
V(Pi)={x∈Ω|d(x,Pi) i,j∈In={1,2,…,N}} (1) 在特定区域Ω中,Pi表示区域Ω中的种子点,d表示任意点到种子点的距离,V(Pi)表示以Pi为种子点的Voronoi单元,其示意图见图1。 (a)二维Voronoi图 (b)三维Voronoi图 利用三维建模软件Rhino 6内置的Grasshopper插件对不规则多孔结构进行建模,均匀不规则多孔结构的设计流程图见图2。首先确定空间中的设计域,在该区域中生成规则点阵,接着以规则点阵中的每个点为中心生成概率球并在球内随机生成新的点,将新的随机点作为种子点对设计域进行Voronoi剖分,最后以Voronoi多边形的边线为基础生成多孔结构。这种设计方法主要涉及不规则度ε、种子点数N和缩放系数K3个变量[11]。 (a)确定设计域 (b)分布规则点阵 (c)以每个点阵为中心生成概率球 在本文的研究中,将不规则度ε固定为0.5。由文献[11]可知,种子点数N对多孔结构孔隙率基本没有影响。孔隙率P与缩放系数K之间成线性关系(图3),缩放系数K增大,多孔结构支杆直径减小,孔隙率增大。 图3 孔隙率P与缩放系数K之间的关系 由1.1节可知,3个设计参数中,缩放系数K通过调节多孔结构支杆直径的方式控制孔隙率,不规则度为定值,种子点数对孔隙率的影响较小,因此可以通过控制缩放系数K来改变支杆直径大小,实现孔隙率的梯度变化。 本文在多孔结构z方向上实现梯度分布。在保证可制造性的前提下,取较大的孔隙率变化范围,缩放系数K的变化范围设置为0.5~0.75。为了避免随机性对实验结果的影响,每个方向上取10个种子点[17],每个种子点在3个方向的距离为4 mm,最后模型的设计尺寸为40 mm×40 mm×40 mm,如图4所示。 图4 梯度多孔结构三维模型 为了模拟自然界和工程应用中各种复杂的梯度变化方式,本文设计了4种不同梯度变化方式的多孔结构,分别是线性函数(Lin),二次函数(Quad)以及两种不同梯度变化率的S形函数(Sig),表达式分别为 P(z)=az+b (2) P(z)=az2+bz+c (3) (4) 其中,z表示模型高度方向上的位置,式(4)(S形函数)中的a、b分别控制梯度多孔结构的起始孔隙率和变化范围,c控制梯度变化率,S形函数的两种梯度变化方式分别记为Sig1和Sig2(图5a)。 如图5所示,对4种函数在水平方向进行10等分,将每等分处的纵坐标值分别赋给10层种子点的缩放系数K,以实现孔隙率在高度方向上的梯度分布。设计4种梯度变化方式的模型如图6所示。 (a)z方向上缩放系数与种子点层号之间的关系 (a)Sig1 (b)Sig2 根据种子点层数将设计模型等分成10层,计算每层的孔隙率并拟合4种函数(图7)以检验设计的可靠性。拟合4种函数的相关系数R2均接近于1,拟合结果良好。缩放系数K与层号q的关系以及孔隙率P在高度方向(z)的梯度变化关系见表1。 表1 4种梯度变化方式函数表达式 (a)等分成10层的梯度多孔结构 使用光固化成形设备(Lite 600,上海联泰科技有限公司)制造实验样品,材料为白色树脂C-UV9400A(东莞爱的合成材料科技有限公司),具体工艺参数为:层厚0.1 mm,扫描间距0.07 mm,扫描速度4000 mm/s。所有类别的模型均打印3个样品。 对4种不同梯度多孔结构试样分别进行纵向(载荷方向平行于梯度方向)和横向(载荷方向垂直于梯度方向)压缩实验(图8),同时加入一组孔隙率相近的均匀多孔结构进行对比。压缩实验遵循GB/T 1041-2008国家标准,压缩设备采用TSE504D(深圳万测试验设备有限公司),压缩速度为1 mm/min,并以50 Hz的频率采集实验数据,用摄像机记录所有试样的压缩过程,并获得其工程应力-应变曲线。弹性模量通过拟合工程应力-应变曲线在弹性阶段的斜率获得。 (a)纵向压缩 (b)横向压缩 由于4种不同变化方式的梯度多孔结构压缩变形特点相似,因此以Lin型梯度多孔结构为例介绍其变形特点。选取应变ε为0、0.1、0.3、0.6时压缩过程的图像进行分析,如图9所示。在应变为0.1时可以观察到多孔结构支杆的屈服变形,纵向压缩时的变形主要发生在高孔隙率部分。在应变为0.3时,已有部分支杆出现断裂失效,纵向压缩时高孔隙率部分的多孔结构表现出致密化的趋势。在应变为0.6时,支杆基本上完全破坏,并逐渐致密化。梯度多孔结构横向压缩变形特点与均匀多孔结构十分相似,都是整个模型均匀地发生变形。这主要是因为这两种结构在载荷方向上的孔隙率都是均匀的,这也说明在横向压缩过程中梯度结构不会改变多孔结构的变形特点。而在纵向压缩时,梯度多孔结构则表现为从高孔隙率部分逐渐向低孔隙率部分坍塌变形,这主要是因为高孔隙率的多孔结构支杆直径更细,结构强度更低,更容易失效。梯度不规则多孔结构在纵向压缩时的变形特点与其他研究中的梯度规则多孔结构相似[18-19]。 图9 不同应变下均匀和Lin型梯度多孔结构压缩变形图 4种不同梯度变化方式的多孔结构纵向压缩和横向压缩的应力-应变曲线见图10,其中,(1)、(2)、(3)表示3次重复性实验的数据。从图10中的曲线可以清楚地分辨出线弹性阶段、平台阶段和致密化阶段[1]。在平台阶段横向压缩时应力基本不变,纵向压缩时应力则表现为逐渐上升的趋势。在平台阶段结束后进入致密化阶段,致密化阶段起始应变通过能量吸收效率法确定[20-21],根据多孔结构压缩的应力-应变曲线,能量吸收效率η可定义为 (a)Sig1 (b)Sig2 (5) 将能量吸收效率最大时的应变作为致密化起始应变,即 (6) 式中,σ为应力;εcd为致密化阶段的起始应变。 4种不同梯度变化方式的多孔结构致密化阶段的起始应变见表2,此时支杆完全破坏并相互接触,致密化的多孔结构与实体相似,应力快速上升。对于同一种梯度变化方式的多孔结构,在小应变阶段,横向压缩时的应力相比纵向压缩时的应力更大;随着应变的增大,纵向压缩的应力逐渐增大并超过横向压缩的应力。纵向压缩中,梯度不规则多孔结构在平台阶段的应力-应变曲线并没有出现像梯度规则多孔结构那样的明显“台阶”状[8,18-19],主要因为本文设计的梯度不规则多孔结构孔隙率变化更加平滑,结构上没有明显的分层。 表2 4种不同变化方式的梯度多孔结构纵向和横向压缩力学性能 在纵向压缩过程中,Sig1型和Sig2型梯度多孔结构在应变为0.15左右时,应力出现一个小幅度下降随后又快速上升。由图7b可知多孔结构梯度按S形函数变化时,高孔隙率的多孔结构占整体结构的比重更大,高孔隙率的多孔结构杆径更细,孔隙更大,压缩过程更容易因结构失效而出现失稳的情况,从而导致应力出现一个短暂的下降。同时S形函数梯度方式的多孔结构从高孔隙率过渡到低孔隙率变化斜率更大,高孔隙率结构致密化后直接进入低孔隙率部分的变形阶段,低孔隙率的多孔结构孔隙更小,支杆变形后更容易相互接触,从而导致应力的快速上升。相比而言,Lin型和Quad型梯度多孔结构高孔隙率部分占比较少而且从高孔隙部分到低孔隙率部分过渡比较平缓,则没有出现这种情况。 4种不同梯度变化方式的多孔结构的纵向和横向压缩的力学性能见表2。对于梯度变化方式相同的多孔结构,横向压缩时的弹性模量和屈服强度均大于纵向压缩的弹性模量和屈服强度,主要是因为纵向压缩时多孔结构从强度较小的高孔隙率处开始变形,而横向压缩时低孔隙率和高孔隙率处的材料同时发生变形,低孔隙率部分具有更好的强度,使得整体结构在压缩过程中表现出更高的弹性模量和屈服强度。在平均孔隙率相近的情况下,改变梯度变化方式并不会对纵向和横向压缩的弹性模量和屈服强度造成太大的影响。Quad型梯度多孔结构由于平均孔隙率最低,故其弹性模量和屈服强度都最大。 4种不同梯度变化方式的多孔结构横向和纵向压缩应力-应变曲线对比见图11。由图7b可知Sig1和Sig2型多孔结构相比于Lin型多孔结构在上半部分具有更高的孔隙率,在下半部分具有更低的孔隙率,这导致了在纵向压缩中,平台阶段Lin型多孔结构在低应变时的应力大于Sig1型和Sig2型多孔结构,随着应变的增大,Sig1型和Sig2型多孔结构的应力值逐渐超过Lin型多孔结构的应力值。对于横向压缩,在平均孔隙率相近情况下,改变梯度变化方式对应力-应变曲线几乎没有影响。Quad型多孔结构几乎在每一层的孔隙率均低于其他3种梯度多孔结构,因此在相同应变下的应力大于其他结构的应力。 (a)纵向压缩 Gibson-Ashby模型是由大量实验和有限元分析结果总结得到的经验公式,是描述多孔结构力学性能和体积分数关系的重要数学模型,常用来预测均匀多孔结构弹性模量: E=EsCωn (7) 式中,Es为基体材料的弹性模量;ω为多孔结构的体积分数;C、n为常数。 通过对6组不同体积分数的均匀多孔结构进行压缩实验来确定本文均匀不规则多孔结构的Gibson-Ashby模型,如图12所示,表达式为 图12 弹性模量E与体积分数ω之间的关系 E=865.15ω1.75 (8) 结合表1中孔隙率与高度的关系,可以得到梯度多孔结构在不同高度上的弹性模量: E(z)=865.15(1-P(z))1.75 (9) Gibson-Ashby模型对多孔结构弹性模量的表征没有考虑结构内部存在梯度的情况,无法准确预测梯度多孔结构的弹性模量[18]。本文将梯度多孔结构看成由n层具有不同弹性模量材料组合而成的复合材料,如图13所示。 (a)纵向压缩 (b)横向压缩 对于纵向压缩,假设每层材料受到的应力相等,采用等应力复合模型预测其弹性模量: (10) 对于横向压缩,假设每层材料受到的应变相等,采用Voigt模型预测其弹性模量: (11) 式中,Eg为整个梯度多孔结构的弹性模量;fi为第i层等效材料所占整个模型的体积分数;Ei为第i层等效材料的弹性模量。 连续分布的梯度多孔结构弹性模量可以通过积分求得,将式(9)代入式(10)、式(11)并进行积分可得 (12) (13) 将表1中的孔隙率与高度之间的函数关系代入式(12)、式(13),将获得的预测结果与实验结果作对比,如表3所示。从表3中能够发现,预测值与实验值的相对误差基本在10%之内,预测结果良好,但相比于文献[18]中的梯度规则多孔结构,本文的预测结果相对误差较大,这可能是由不规则多孔结构的随机性所导致。从预测结果来看,在横向压缩中,梯度变化方式对多孔结构弹性模量基本没有影响,这与实验所表现的结果一致。Quad型梯度多孔结构具有更高的弹性模量,说明增加低孔隙率的多孔结构所占比重,能够提高梯度多孔结构的弹性模量。 表3 弹性模量预测结果和实验结果对比 本文利用参数化设计插件Grasshopper设计了4种不同梯度变化方式的不规则多孔结构,利用光固化成形工艺制备这4种梯度多孔结构,并进行纵向和横向压缩实验,分析其变形特点和力学性能,主要有以下结论: (1)通过控制缩放系数K在高度方向上的梯度分布,设计了4种不同梯度变化方式的多孔结构,设计结果与预期符合良好。 (2)梯度多孔结构横向压缩的变形特点与均匀多孔结构相似,表现为整体结构的均匀变形破坏,纵向压缩表现出逐层坍塌的变形特点。 (3)横向压缩时应力-应变曲线在平台阶段的应力基本不变,纵向压缩时平台阶段的应力逐渐上升。对于平均孔隙率相近的梯度多孔结构,改变梯度变化方式能够影响纵向压缩的应力-应变曲线和力学性能,但对横向压缩则基本没有影响。降低梯度多孔结构的平均孔隙率可以显著提高多孔结构的弹性模量和屈服强度。 (4)将梯度多孔结构看成复合材料,通过等应力复合模型和Voigt模型并结合Gibson-Ashby模型可以有效预测梯度多孔结构纵向压缩和横向压缩的弹性模量,相对误差基本都在10%以内。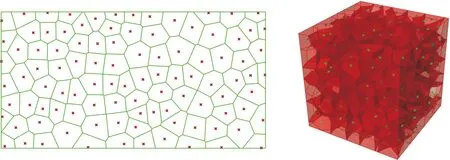
1.2 梯度不规则多孔结构设计



1.3 不规则多孔结构制造与压缩实验
2 结果与分析
2.1 变形特点

2.2 力学性能
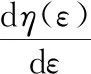
2.3 弹性性能预测
3 结论

