梯度空心多孔结构优化设计方法

田启华 舒正涛 付君健 杜义贤 周祥曼 田 磊

1.三峡大学机械与动力学院，宜昌，443002

2.水电机械设备设计与维护湖北省重点实验室，宜昌，443002

0 引言

空心多孔结构是基于实心多孔结构改进的新形式，以实心多孔结构为基础，去除内部材料，保留一定外壳厚度，实现结构的空心化[1]。空心多孔结构具有承载、吸能、吸声以及隔振等优良的性能[2-5]，广泛应用于汽车、船舶和航空航天等领域。然而传统的建模方法难以实现空心结构复杂的几何特征描述，且均匀的周期性结构无法充分发挥其力学性能，在实际工程应用中存在一定的局限性，因此，需要进一步探索和发展空心多孔结构参数化建模技术，实现结构功能特性的调控。

先进制造技术的发展为空心多孔结构的应用提供了强有力的支撑。目前，可采用焊接成形[6-7]、热膨胀模塑成形[8]和增材制造[9-10]等技术，制备出菱形、金字塔型、四面体型及三周期极小曲面等空心多孔结构。空心多孔结构压缩和剪切工况是工程应用中最常见的应用场景，通过研究不同材料的单胞构型发现，空心多孔结构的压缩和剪切强度优于实心多孔结构，特别是面外压缩强度，是相同密度下实心多孔结构的2倍以上[6-7]。有限元数值仿真也表明，相对密度为0.9%～5.8%的空心金字塔型多孔结构的压缩和剪切强度可达相同密度实心多孔结构的3～5倍[11]。尽管在空心多孔结构的制备上具有成熟的制造技术，但目前涉及空心多孔结构的优化设计方法较少[12-13]。大多研究都采用形状单一的空心圆管或者方管进行设计，通过调整空心杆件的尺寸、偏角或壁厚等几何参数，实现空心多孔结构力学性能的调控[1，4，14]。然而，空心多孔结构的力学性能与其几何构型存在复杂的耦合关系，进一步研究参数化建模技术，实现空心多孔结构参数对几何构型和力学性能的调控是一个亟待解决的关键问题。

此外，空心多孔结构的分布形式对力学性能也有重要的影响。相对密度均匀的周期性多孔结构无法充分发挥空心结构单胞的性能优势，通过空心多孔结构的梯度设计可进一步提高空心结构力学性能。功能梯度多孔结构的性能依赖于周期性细/微观结构的拓扑构型，无需改变结构的材料组分即可实现结构特定的功能设计[15]。一些学者提出了关于极小曲面的功能梯度多孔结构建模方法，如B样条插值曲线和多项式插值函数[16-17]等，实现了多孔结构的梯度渐变。梯度多孔结构的设计实际上是考虑设计域内材料属性的连续变化，本质上与拓扑优化方法类似[18-19]，故可利用拓扑优化方法开展梯度多孔结构设计[20-21]，如密度映射方法[22-23]、材料/结构一体化优化设计方法[24-25]等。上述几类方法丰富了梯度结构的设计理论和工程应用，但仍存在一些亟待解决的问题，如多孔结构整体体积分数不易准确控制、结构边界连续性难以保证。需要说明的是，上述研究大多侧重于梯度结构吸能特性的提升，结构的承载性能还存在一定的不足[26]。因此，引入性能更优的空心多孔结构单胞，研究稳定、高效的梯度空心多孔结构优化设计方法，将为空心多孔结构的创新设计和承载性能的提升提供一个新的思路。

为实现空心多孔结构的参数化建模、提高多孔结构的承载性能，本文提出了一种梯度空心多孔结构优化设计方法。对I-WP型三周期极小曲面进行布尔运算，实现了空心多孔结构单胞的隐式建模；通过构造混合水平集函数，建立了梯度多孔结构的参数化模型；利用水平集演化出空心多孔结构在空间中最优材料分布形式，得到了具有良好连续性和优良承载性能的梯度空心多孔结构，并通过数值案例和实验验证了本文所提方法的可行性与有效性。

1 I-WP型空心多孔结构参数化建模

水平集方法的基本思想是将曲线(或曲面)隐式地表达为一个高维函数Φ(X)的等值面，通过追踪高维函数Φ(X)的运动来达到描述曲线(或曲面)变化的目的[27]。其数学表达式为[28]

∂Ω(X)={X：Φ(X)=0，X∈D}

(1)

式中，X为高维空间的物理坐标；D为包含曲线∂Ω(或曲面的)的空间；Ω为几何结构的实体区域；∂Ω为实体区域与空洞区域的边界。∂Ω=ΓD∪ΓN∪Γf，包含Dirichlet边界ΓD、Neumann边界ΓN和无牵引力边Γf。

水平集函数隐式地描述了结构形状Ω，定义如下：

(2)

图1所示为水平集函数的隐式描述方式，对于三维的结构边界，需要四维的水平集函数来描述。

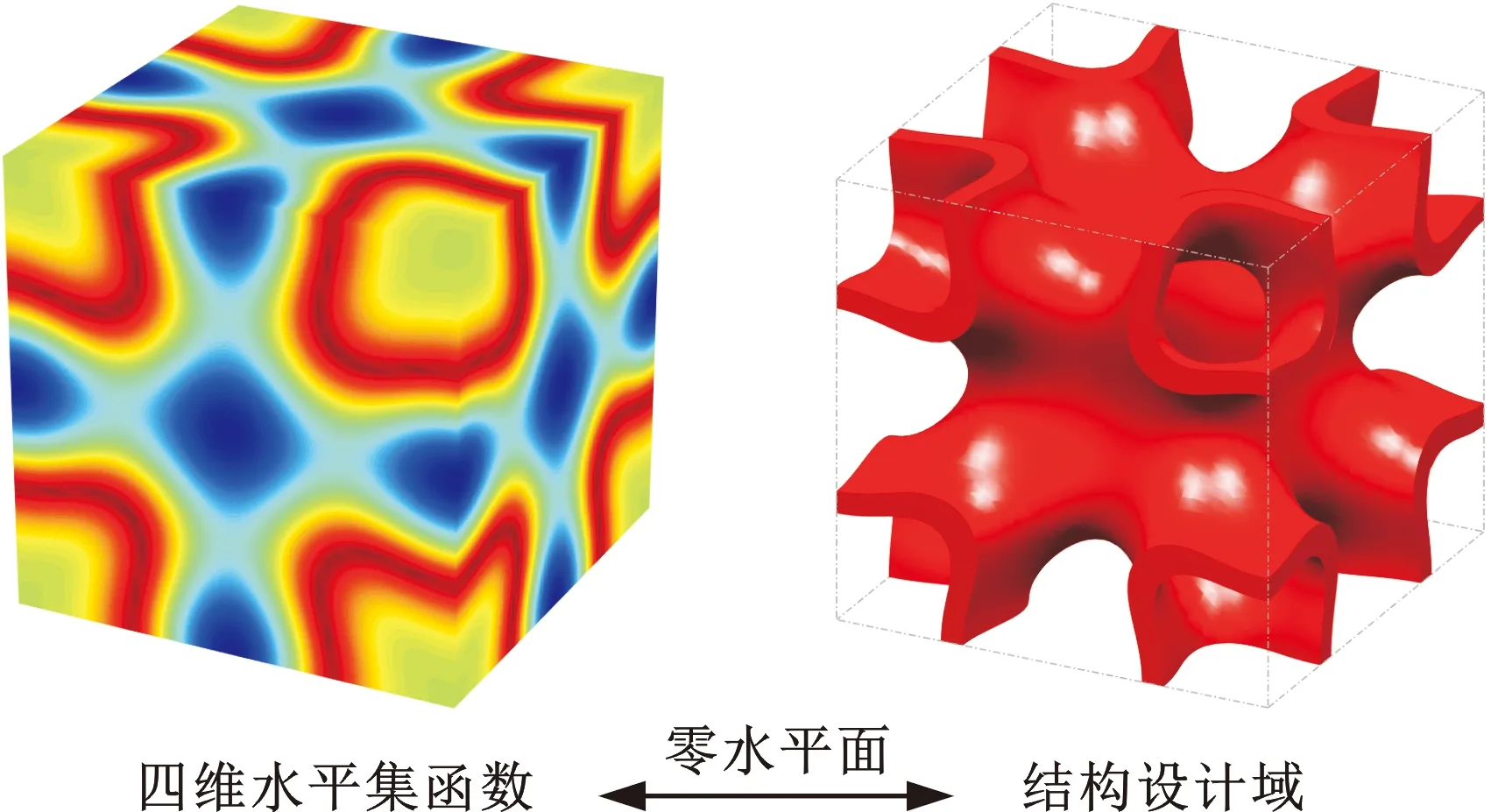
图1 四维水平集函数及零等值面

三周期极小曲面结构具有低密度、高比强度、设计性强的结构优势以及良好的制造优势，如具备自支撑能力、良好的排屑性能[29]，是梯度多孔结构的主要代表性体积单胞之一。本文将采用I-WP型极小曲面作为宏观结构的代表性体积单胞，实现梯度空心多孔结构的参数化建模。

极小曲面的数学表达式是一种三维隐式水平集函数，在I-WP型极小曲面函数中引入水平参数r可控制极小曲面体积分数的变化[30]，其表达式为

(3)

式中，ФI(x，y，z，r)为极小曲面数学表达式；x，y，z为高维空间的物理坐标；L为极小曲面单胞的边长。

为了设计I-WP型空心多孔结构，定义两个I-WP型极小曲面，水平参数分别定义为r1和r2，得到两个体积分数不同的极小曲面多孔结构。将水平参数为r2的极小曲面多孔结构作为基础结构，通过差集布尔运算，得到I-WP型空心多孔结构的数学表达式[31]。差集布尔运算的数学表达式为

Φ=min(Φ(x，y，z，r2)，-Φ(x，y，z，r1))

(4)

通过调整水平参数r1可以得到不同壁厚的空心单胞，布尔运算过程如图2所示。

图2 I-WP型空心多孔结构布尔运算过程

极小曲面是隐式函数，其隐式特性使其具有布尔运算简便、结构边界清晰、拓扑可变能力强等特点，与CAD/CAE等软件的结合也较为方便。将水平集函数的零等值面转化为模型三角面片的几何信息即每个三角面片的法矢量和顶点坐标，由此可得到二进制STL文件，进而对模型进行后处理。模型后处理过程如图3所示，首先对原始STL模型表面三角面片上存在的孔洞、缝隙、重叠或相交等缺陷进行修复，使其满足模型实体化要求；再将模型表面三角面片缝合，形成实体。实体化是模型在CAD软件中进行布尔运算、打孔、修剪等操作的前提，实体化后的模型也便于与CAE软件结合，进行力学仿真等操作。

图3 I-WP型空心多孔结构模型处理

2 空心多孔结构弹性性能分析

为说明I-WP型空心多孔结构的性能优势，采用数值均匀化法[32]计算I-WP型空心多孔结构和实心多孔结构的等效弹性矩阵，揭示空心多孔结构的宏观等效力学特性。

多孔结构等效弹性张量CH的表达式为

(5)

式中，|V|为单胞的体积；Ve为单元e的体积；I为六阶单位矩阵；Be为单元应变-位移矩阵；χe为单元位移向量；De为单元本构矩阵。

基于I-WP型空心多孔结构的高度对称性，其等效弹性矩阵可以简化为

(6)

使用等效弹性矩阵中的分量来计算多孔结构的等效弹性模量EH、等效剪切模量GH和等效泊松比υH：

EH=(C112+C11C12-2C122)/(C11+C12)

(7)

GH=C44

(8)

(9)

刚度θ作为多孔结构弹性性能的度量指标[33]：

(10)

(11)

(12)

(13)

(14)

式中，EHSU、GHSU和νHSU分别为引入HS理论极限的体积模量、剪切模量和泊松比；ρ为多孔结构的相对密度；Gb、Kb分别为材料的剪切模量和体积模量。

式(10)～式(14)中，取材料弹性模量(量纲一化)为1，泊松比为0.3，则Gb=1/2.6，Kb=1/1.2。

采用I-WP型空心/实心单胞的梯度多孔结构刚度对比数据如图4所示，数据结果表明，I-WP型空心结构在任意体积分数下的刚度均高于实心多孔结构，但随着体积分数的增大，实心单胞刚度逐渐逼近空心单胞。

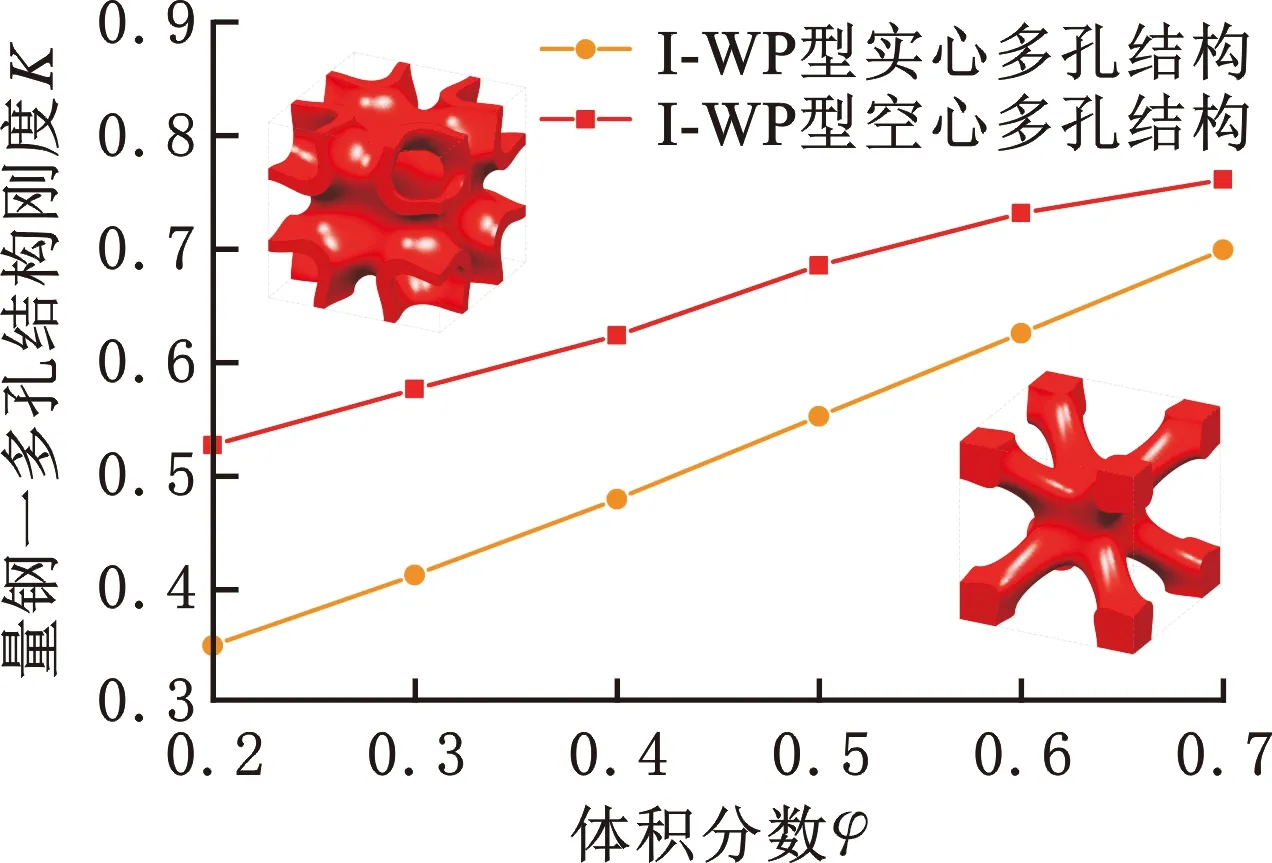
图4 不同体积分数的结构刚度对比

为进一步说明I-WP型空心多孔结构单胞的力学性能优势，分别对体积分数为0.2～0.7的I-WP型空心/实心单胞进行有限元分析。材料设置为尼龙PA2200，与后续的仿真和实验材料保持一致。具体材料属性如下：弹性模量741 MPa，屈服强度54 MPa，泊松比0.3，密度1020 kg/m3。多孔结构单胞的边界条件如图5a所示，单胞下平面为固定约束，上平面施加竖直向下的均布载荷，F=500 N。

在相同载荷下，两种结构产生的最大位移与最大应力对比如图5b、图5c所示。单胞位移与应力变化趋势较为相似，随着体积分数的增大，空心、实心单胞的性能差距逐渐缩小，但空心单胞产生的位移与应力始终比实心单胞小，说明了空心多孔结构单胞具有更优良的力学性能。

(a)边界条件

3 空心多孔结构混合水平集描述

3.1 混合水平集函数构造

三周期极小曲面多孔结构采用参数化数学函数进行几何描述，具有较强的可设计性[16]：①通过调整极小曲面单胞的边长L或水平控制参数r，可控制极小曲面构型和体积分数的变化；②对不同类型的三周期极小曲面进行混合设计，可得到具有新型结构特征的多孔结构。基于以上特点，可以引入凸优化理论中的仿射概念[34]：对于集合Q⊆R，如果通过集合Q中任意两个不同点之间的直线仍然在集合Q中，则称集合Q为仿射集。

利用相似的概念，对两种不同的空心极小曲面结构的混合设计过程进行定义，其数学表达式为

ΦH=sΦ1+(1-s)Φ2

(15)

式中，ΦH为具有新型结构特征的空心极小曲面函数；Φ1和Φ2为两种预定义的空心极小曲面水平集函数；s为设计参数，即两种预定义空心极小曲面结构的相对权重。

基于式(15)，预定义两种空心多孔结构单胞的水平集函数，并引入权重系数，构造梯度空心多孔结构的混合水平集函数，实现多孔结构的参数化建模。采用隐式水平集函数进行结构几何描述：

(16)

式中，w(t)为权重系数矢量，是关于宏观时间t的变量，每一元素值取值范围为[0,1]；x为设计域D的内空间物理坐标；φ1(x)和φ2(x)分别为预定义的两种空心多孔结构单胞的水平集函数。

通过调整权重系数w(t)，可以灵活地控制空心多孔结构单胞的壁厚，同时改变了单胞的体积分数。为进一步说明权重系数对空心多孔结构单胞壁厚和体积分数的影响，预定义两个量纲一尺寸为50×50×50的空心多孔结构单胞，根据式(3)、式(4)，定义可变水平参数r1为13.3、-4.69，固定参数r2=-11，得到两个空心多孔结构单胞φ1(x)和φ2(x)，其体积分数为0.7、0.15，单胞壁厚分别为10.44、1.94(量纲一单位)。通过调整权重系数发现，权重系数对单胞壁厚的影响程度主要分为三个阶段，即权重系数为0～0.2、0.3～0.8、0.9～1。权重系数与单胞壁厚、体积分数的详细关系如表1所示。I-WP型极小曲面空心单胞几何特征较为复杂，因此，权重系数和单胞壁厚并不是严格的线性关系。

表1 权重系数与单胞参数关系

3.2 梯度空心多孔结构C0连续性建模

在梯度空心多孔结构设计过程中，良好的连续性是多孔结构的力学性能与后期制造性能的基本保障[35-36]。为了保证多孔结构边界的连续性过渡，本文基于混合水平集方法构造全局更新-局部插值的设计变量更新策略，实现梯度空心多孔结构C0连续性建模。

将设计域离散为M个单胞，具有m个节点。任意一个单胞C可以进一步离散为若干八节点六面体单元，如图6所示。

图6 设计域离散与设计变量定义

全局设计变量可表示为[35]

w(t)=[w1(t)w2(t) …wm(t)]Τ

(17)

式中，w(t)为定义在单胞节点上的宏观设计变量，即全局权重系数；m为设计域单胞节点数，即全局设计变量的数目。

对于编号为C的三维多孔结构单胞，8个节点上的权重系数是全局权重系数向量的子向量：

(18)

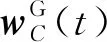
(19)

式中，省略位置的数值均为0。

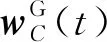
(20)

对于八节点六面体线性单元，其形函数Ni定义为

(21)

其中，i(i=1，2，…，8)为单元节点序号，ξ0=ξiξ，η0=ηiη，ζ0=ζiζ，ξi=±1，ηi=±1，ζi=±1，ξ、η、ζ为局部坐标系下单元内部点坐标。

单胞C上所有节点的权重系数wC(t)可表示为

(22)

在不添加额外的几何约束或对优化结构进行后处理的情况下，结构边界会出现几何突变，相邻单胞边界的连续性无法得到保证，如图7a所示。由图6所示的设计变量定义可知，相邻单胞在公共节点上定义了相同的权重系数，对全局权重系数进行插值时，能够自然地保证线性插值函数的连续性，进而实现了梯度多孔结构C0连续，而不需要添加额外的几何约束。图7b所示为引入插值策略后的梯度多孔结构，可以发现，相邻空心结构单胞边界具有良好几何连续性，实现了单胞壁厚的连续渐变。

(a)原始梯度空心多孔结构

4 拓扑优化数学模型与灵敏度分析

4.1 拓扑优化数学模型

以结构刚度性能为目标函数，多孔结构体积分数为约束条件，建立基于混合水平集方法的梯度空心多孔结构拓扑优化数学模型：

(23)

弹性平衡方程的弱形式中，能量双线性形式aФ(u，v)和载荷线性形式lФ(v)分别为

(24)

(25)

其中，f为应用在边界∂Ω上的牵引力，p为体积力，|Ф|为水平集函数梯度的模。δ(Ф)为Dirac函数，是Heaviside函数的导数形式：

(26)

这里，γ=0.001，Δ为Heaviside函数近似的半带宽。

4.2 灵敏度分析

本文采用形状导数敏度[15，37]分析方法推导目标函数、能量双线性形式、载荷线性形式关于宏观时间变量t的微分形式，进一步化简为

(27)

(28)

式中，vn为法向速度；n为法向单位向量。

以全局权重系数w(t)作为设计变量，对Hamilton-Jacobi偏微分方程进行时空解耦，从而将水平集函数参数化。将混合水平集函数代入Hamilton-Jacobi偏微分方程，得到仅关于时间t的常微分方程，其数学表达式为

(29)

可得水平集函数边界演化的法向速度：

(30)

将式(30)代入式(27)得

(31)

采用链式法则对目标函数J(Φ)直接求其关于时间变量t的导数：

(32)

比较式(31)和式(32)可以得到目标函数J(Φ)关于设计变量w(t)的灵敏度：

(33)

同理得到体积约束g(Φ)关于设计变量w(t)的灵敏度：

(34)

5 数值案例

梯度空心多孔结构设计流程如图 8所示。首先对I-WP型实心单胞进行布尔运算，获得空心单胞，再利用混合水平集函数实现多孔结构参数化建模，最后求解拓扑优化模型，得到几何和功能在空间呈梯度分布的空心多孔结构。

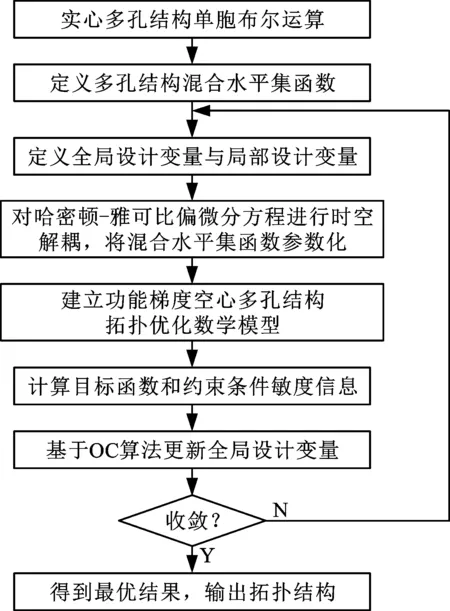
图8 梯度空心多孔结构设计流程

本文将采用OC(optimality criteria)作为优化求解算法，对数学模型进行求解。OC算法具有简单直接、迭代收敛快的特点，对单约束条件下的大规模结构优化设计问题求解尤为高效[38]。在优化算法中，给定收敛准则如下：

(35)

式中，J为目标函数值；n为当前迭代步数；nmax为最大迭代步数。

为了验证本文提出方法的可行性与有效性，分别基于I-WP型空心和实心多孔结构单胞，给出三维悬臂梁梯度多孔结构拓扑优化算例。在本节的优化过程中，本文给出的量均为量纲一单位，在有限元分析中，按照实际模型尺寸以及负载为参数给出了相应的刚度。

5.1 采用空心多孔结构单胞的悬臂梁结构优化

图9所示为三维悬臂梁结构设计域，设计域长宽高分别为L=120，W=20，H=50。设计域的右端面为固定约束，上平面距离左边界L/12处施加竖直向下的均布载荷F=-10。设计域离散为12×2×5个单胞，每个单胞进一步离散为50×50×50个八节点六面体单元。设计域体积分数约束为0.45。选取I-WP型空心多孔结构作为预定义多孔结构单胞，如图10所示，其体积分数分别为0.2、0.6，单胞外形尺寸一致，壁厚尺寸不同。

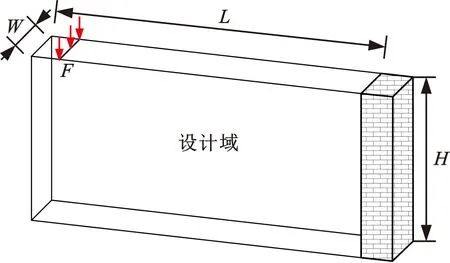
图9 三维悬臂梁设计域

图10 预定义空心多孔结构单胞

图11所示为采用I-WP型空心单胞的悬臂梁拓扑优化迭代曲线，随着优化的进行，结构柔度逐渐减小，经过61次迭代后，结构柔度从15 064.27收敛至8551.08，体积分数收敛至0.45。根据优化迭代曲线可知，提出的梯度空心多孔结构混合水平集优化算法运行稳定，收敛性较好。

图11 采用I-WP型空心单胞的悬臂梁结构优化迭代曲线

悬臂梁结构最优构型如图12所示，结构轮廓清晰，在主要传递力路径上，空心单胞壁厚较厚，其他区域空心单胞体积分数较小，保留最小壁厚尺寸。优化后的结构在几何上和密度上呈现出明显的梯度分布，单胞自身根据外部载荷和边界条件在空间中表现出不同的方向梯度。从这个意义上说，该方法不仅获得了结构最佳材料空间分布，还实现了最优梯度单胞构型设计。此外，在优化过程中，由于相邻单胞公共节点上的权重系数是相同的，故保证了线性插值函数的连续性，从而实现了单胞几何边界的连续过渡，也使得优化后的梯度空心多孔结构具有较好的力学性能。

图12 采用空心单胞的悬臂梁最优拓扑构型

设计域中单胞的梯度变化是通过单胞节点上的权重系数控制的，在结构主要的传递力路径上，权重系数分布的数值较大，生成壁厚较厚的单胞。对于设计域中承载作用贡献小的区域，权重系数分布的数值较小，从而填充薄壁单胞。在传统的拓扑优化中，优化后的结构只保留了受力材料，当传递力路径位置上的材料被破坏时，会严重影响结构整体的力学性能[16]。而在本文所提出的方法中，通过控制预设单胞的体积分数，使得设计域内分布一系列壁厚不同的空心梯度单胞，极大地提高了结构稳定性和整体刚度性能。

5.2 采用实心多孔结构单胞的悬臂梁结构优化

为了说明优化方法的有效性，采用实心多孔结构单胞对悬臂梁结构进行优化设计。选取图13所示的I-WP型实心结构作为预定义多孔结构单胞，其体积分数分别为0.2、0.6。图14所示为采用实心单胞的悬臂梁结构优化迭代曲线，经过61次迭代后，目标函数和体积约束曲线收敛。初始均匀多孔结构的结构柔度为53 731.06，优化后的结构柔度为10 954.80。

图13 预定义实心多孔结构单胞

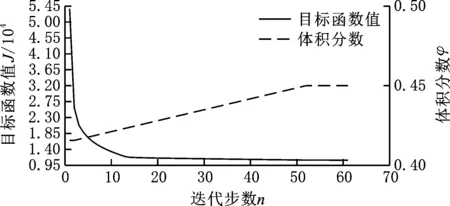
图14 采用I-WP型实心单胞的悬臂梁结构优化迭代曲线

由于预定义的I-WP型实心多孔结构单胞最小体积分数为0.2，故多孔结构被填充到整个设计域内。在传递力路径上的单胞多孔结构单胞的体积分数较大，其他区域则分布较少的材料，结构在几何和密度上也呈现出明显的梯度分布。由图15发现，体积分数不同的单胞边界之间过渡连续，可有效避免多孔结构承载时出现的应力集中现象，也保证了后期的可制造性。

图15 采用实心单胞的悬臂梁最优拓扑构型

在上述两个算例中，分别采用了I-WP型空心和实心单胞对悬臂梁结构进行优化。根据优化结果可知，采用本文提出的混合水平集拓扑优化算法，均可不同程度地提高结构的承载性能，得到几何上和密度上呈梯度分布的多孔结构。根据图11和图14绘制了两种优化后的结构柔度对比图，如图16所示。在结构体积分数设置为0.45条件下，优化后的梯度结构柔度分别为8551.08、10 954.80。优化结果表明，在相同体积分数下，梯度空心多孔结构的承载能力可提高21.94%，说明本文方法具有显著的优化效果。

图16 结构柔度对比

5.3 优化结构的有限元分析

为了对比分析优化后的结构在线弹性范围内的静承载性能，分别对两种结构进行了有限元分析。定义结构的材料为尼龙PA2200，与后续实验样件材料保持一致，在本文第2节中给出了材料属性的具体数值。边界条件按照图9设置，绘制了结构载荷与最大位移曲线，如图17所示。由有限元仿真结果可知，在相同的静载荷下，梯度空心多孔结构的变形位移明显小于相同体积分数的实心多孔结构，表明空心多孔结构的承载性能更优。在线弹性范围内，结构变形量与负载成线性关系，根据载荷-位移曲线可知，采用I-WP型空心和实心单胞的梯度多孔结构整体刚度分别为63.86 N/mm、51.95 N/mm，结构刚度提高了约22.92%。

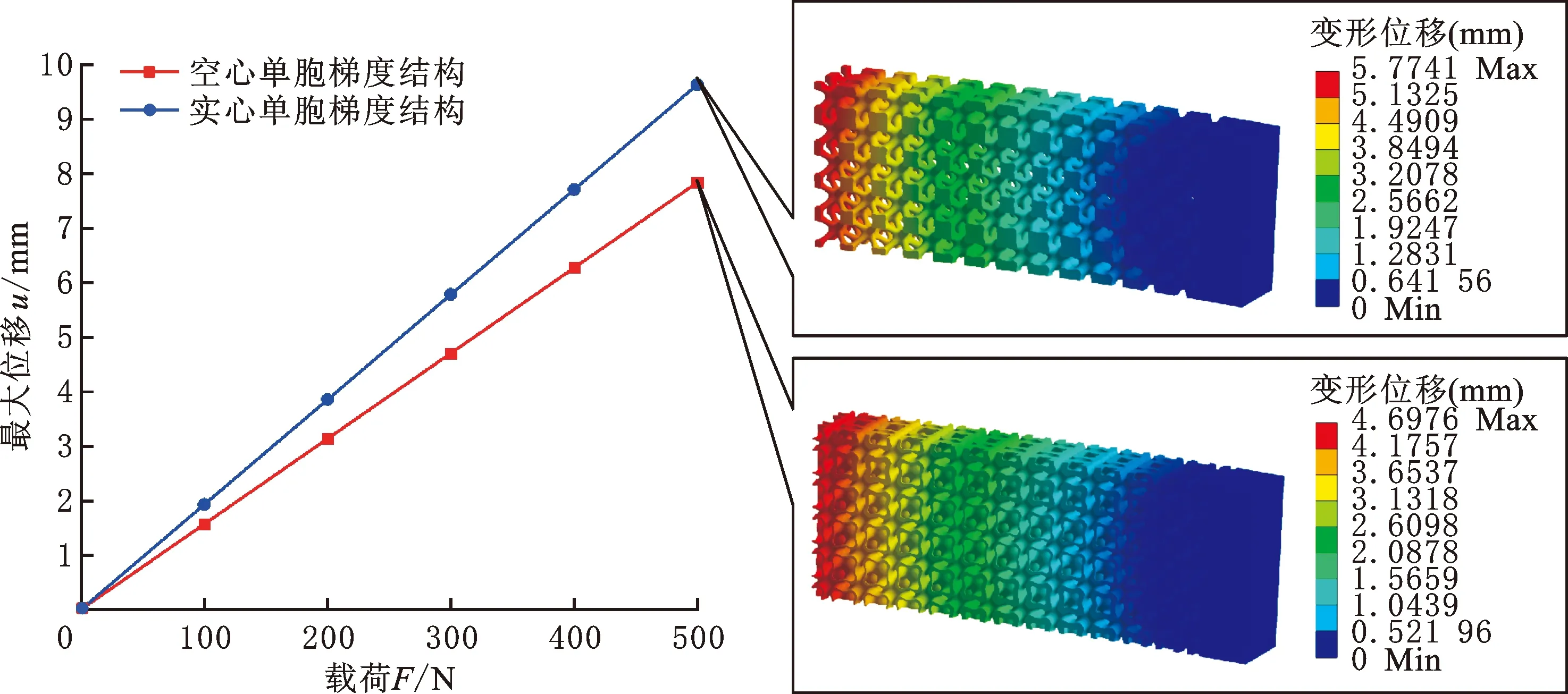
图17 载荷-最大位移仿真曲线

6 悬臂梁结构实验分析

为进一步验证采用空心或实心单胞的梯度多孔结构承载性能，对优化结构进行实验分析，用于实验的模型结构尺寸和体积分数与5.1节中给定的参数保持一致，L=120 mm，W=20 mm，H=50 mm。同时，为了便于夹持和固定样件，在模型右侧设置尺寸为15 mm×20 mm×50 mm的实体区域。选用EOS-P760型3D打印机，采用选择性激光烧结(selective laser sintering，SLS)技术制造了悬臂梁模型样件，结构材料为尼龙PA2200，如图18所示。

(a)采用空心单胞的悬臂梁样件

根据相关实验标准，在室温条件下，采用WDW-100E型电子式万能试验机进行悬臂梁实验。图19所示为样件实验装置，包括夹持样件的台钳、固定台、万能试验机等。在尽可能保证结构边界条件一致的情况下，万能试验机压头以20 mm/min的动态载荷垂直加载，模拟准静态压缩条件，加载时间为30 s。利用万能试验机数据采集系统记录加载过程中的位移和相应的载荷。

图19 实验装置

万能试验机压头向下移动行程约为10 mm，取位移区间0～8 mm为有效行程，样件的实验荷载-位移曲线如图20所示。通过线性回归计算了样件的整体刚度，采用I-WP型空心和实心单胞的梯度结构样件的整体刚度分别为65.89 N/mm、47.92 N/mm。得到的刚度值表明，采用空心单胞的梯度结构刚度性能明显优于采用实心单胞的梯度结构。此外，结构的强度还可以通过在相同变形下承受的载荷大小来评估。如图20所示，当万能试验机压头向下位移达到8 mm时，空心单胞梯度结构承受的载荷为487.4 N，实心单胞梯度结构承受的载荷为383.0 N，说明采用空心单胞的梯度结构具有较好的承载性能。

图20 两种样件的负载-位移曲线

本文分别对两种结构进行了有限元分析与实验研究，仿真与实验的结果具有较好的一致性，其误差均在5%左右。有限元分析结果与实验结果均表明，相较于采用实心单胞的梯度多孔结构，本文所设计的梯度空心多孔结构的刚度和强度有显著提高。

7 结论

本文提出了一种梯度空心多孔结构优化设计方法，对I-WP型三周期极小曲面进行布尔运算实现了空心多孔结构单胞的参数化设计；引入凸优化理论的仿射概念，构造混合水平集函数，实现了梯度空心多孔结构的参数化建模。对优化结构进行有限元仿真分析，并采用选择性激光烧结技术制造了模型样件，开展了力学实验。数值案例和实验结果表明，所提方法能够有效地解决空心多孔结构复杂的几何特征建模问题，显著提高多孔结构的承载性能。在实际工程问题中，结构需要面对复杂的物理场问题，可在本文方法中考虑结构的吸能特性、屈曲稳定性或散热特性等，实现面向多功能、多物理场的梯度空心多孔结构设计。