Bézier单元刚度映射下的高效多重网格等几何拓扑优化方法
丁延冬 罗年猛 杨奥迪 王书亭 朱浩然 谢贤达
华中科技大学机械科学与工程学院,武汉,430074
0 引言
拓扑优化是一种在给定条件约束的设计域进行结构设计的有效工具,被广泛应用于散热结构[1]、柔性机构[2]与弹性结构[3]。经典拓扑优化方法主要有各向同性惩罚微结构法(simple isotropic material with penalization,SIMP)[4]、进化法[5]、水平集法[6-7]、移动可变形组件/孔洞法[8-9]等。有限元法是传统拓扑优化的求解基础,其求解精度对拓扑优化过程的鲁棒性至关重要,而有限元物理场离散形函数的C0连续无法满足应力约束等高阶拓扑优化问题的求解要求。
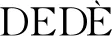
无论是传统有限元拓扑优化程序还是等几何拓扑优化程序,更精确的优化结果均需要规模更大的有限元求解,因此优化过程需消耗大量的计算成本[17]。通过改进有限元求解算法来提高拓扑优化计算效率一直是拓扑优化的研究热点,主要方法有自适应网格法[18-19]和多重网格法[20-22]。WANG等[23]将等几何分析求解精度优势与多重网格求解效率的优势相结合,提出了多重网格等几何优化模型。然而,由于B样条基函数空间的非单元一致性,上述多重网格等几何拓扑优化方法在每一层的拓扑优化过程中需要进行所有B样条单元刚度的计算和存储,进而实现优化过程中等几何单元刚度矩阵的快速更新,导致多重等几何拓扑优化存在数据存储负担过重和预处理时间过长等问题。针对上述问题,可采用Bézier提取算子对B样条单元数据进行预处理,实现任一层级网格B样条基函数通过C0连续且单元空间保持的Bernstein基函数来等效表达。其中,Bézier提取算子作为一种基本的转换方式,被用于保证B样条基函数的高阶连续性,已被广泛应用于等几何分析框架中的T样条[24]、截断层次B样条[25-27]与极样条[28]。
本文提出基于Bézier单元刚度映射的多重网格等几何拓扑优化模型,以实现等几何拓扑优化数据的存储结构和预处理过程效率的优化。通过Bézier提取算子将各层级的所有B样条单元刚度矩阵的大规模存储转换为标准刚度矩阵与各层级Bézier提取矩阵的存储,并将任一层级所有B样条单元刚度矩阵的计算过程转换为任一层级若干个(2或3)参数方向的Bézier提取矩阵的计算过程,进而建立任一层级任一B样条单元刚度矩阵与标准Bézier单元刚度矩阵的映射关系。利用B样条单元刚度矩阵与标准Bézier单元刚度矩阵之间的映射法则,显著降低多重网格等几何拓扑优化的刚度矩阵内存占用并减少刚度矩阵预处理流程的时间消耗。最后,通过二维与三维数值算例的优化结果展示本文模型在内存空间和预处理时间两个方面的优势。
1 理论基础
首先介绍Bernstein多项式,接着对开节点向量生成B样条的递归定义进行回顾,最后基于Bézier分解算法引出Bézier提取算子。其中,Bézier提取算子是实现Bernstein多项式与B样条之间映射的理论基础。
1.1 Bernstein多项式
对于任意位于[0,1]内的参数坐标ζ,相应的p阶Bernstein多项式由以下递推式获得:
Bi,p(ζ)=
(1)
其中,Bi,0(ζ)=1。阶次p=1,2,3的Bernstein基函数如图1所示。
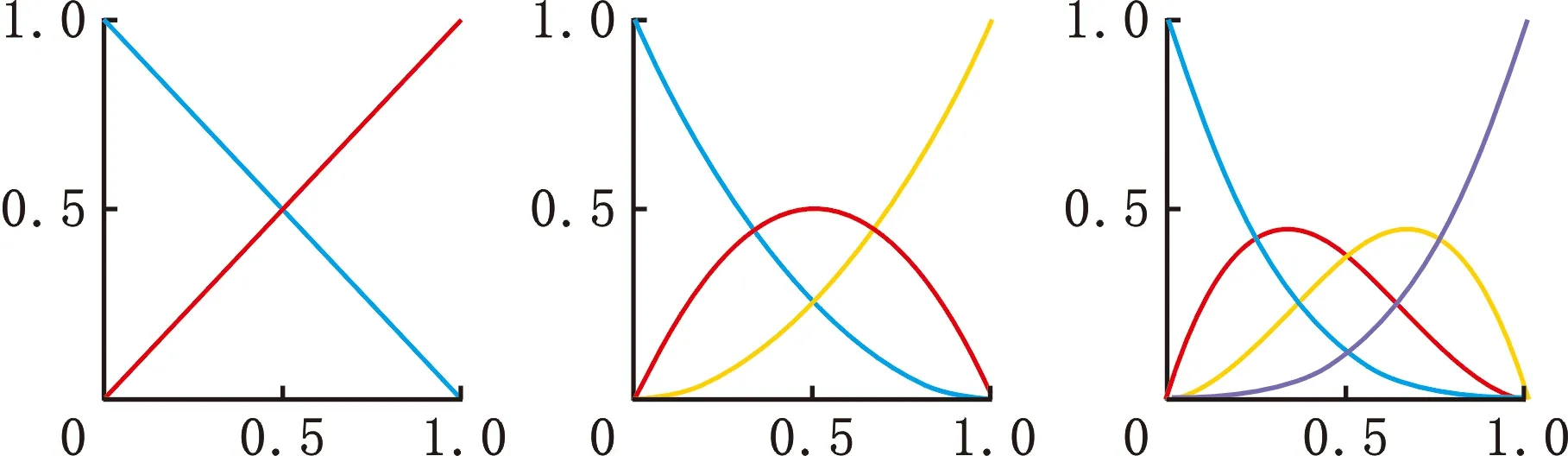
(a)p=1 (b)p=2 (c)p=3
Bézier曲线可以由Bernstein多项式作为基函数并与控制点Pi的线性组合来表达,表达式为
(2)
1.2 B样条
对于给定的开节点向量Ξ=(ζ1,ζ2,…,ζn+p+1),B样条的基函数由Cox-de Boor递推公式定义:
Nj,p(ζ)=
(3)
其中,p、n分别表示B样条基函数的阶次和相应控制点个数。通过组合B样条基函数与控制点可生成B样条曲线,B样条曲线的表达式如下:
(4)
多维参数空间下,B样条基函数由张量积结构生成,因此,二维B样条基函数由以下公式定义:
N(j1,j2),(p1,p2)(ζ,η)=Nj1,p1(ζ)Nj2,p2(η)
(5)
其中,(ζ,η)表示二维参数空间下的参数坐标,jd(d=1,2)、pd(d=1,2)分别表示d维参数方向基函数的索引和阶次。开节点向量(0,0,0,1,2,3,3,3)的B样条基函数空间和各节点向量单元的局部B样条基函数空间如图2所示,图3为图2所示B样条基函数生成的B样条曲线。
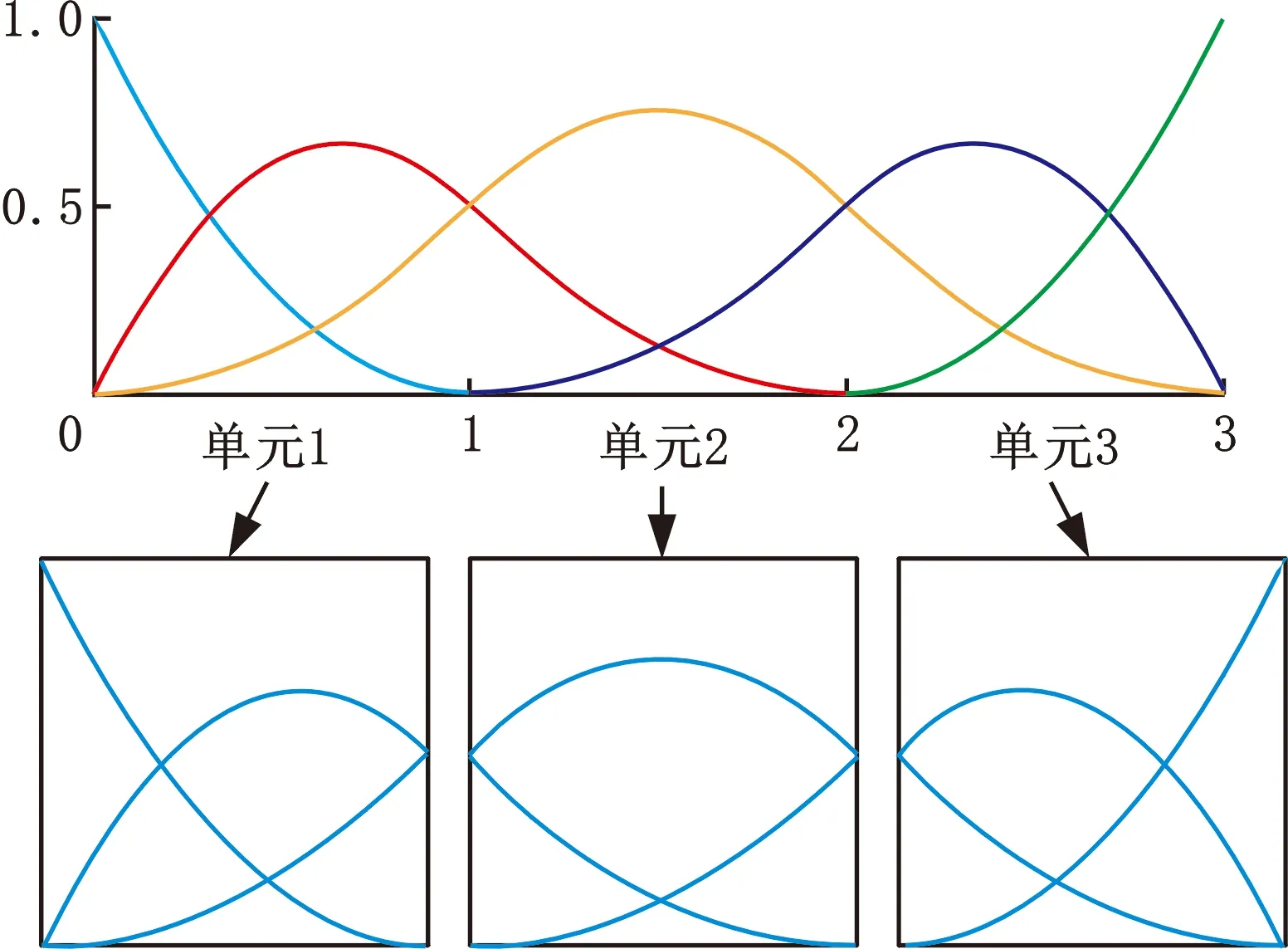
图2 开节点向量(0,0,0,1,2,3,3,3)的2阶B样条基函数

图3 图2中B样条基函数所生成的B样条曲线
1.3 Bézier提取算子
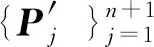
(6)
其中,αj的推导公式为
(7)
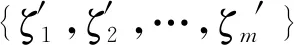
C(k)=
(8)
C(k)∈R(n+k-1)×(n+k)
整体的Bézier提取矩阵由C(k)(k=1,2,…,m)组成,其表达式为
Cext=C(1)C(2)…C(m)
(9)

N(ζ)=CextB(ζ)
(10)
Bézier曲线的控制点PB也可以通过Bézier提取算子从相应B样条控制点P获取,如下式:
(11)
其中,PB的维度为(n+m)×d;P的维度为n×d。
借助于B样条的张量积结构,多变量的Bézier提取算子可方便地从单变量Bézier提取算子生成。双变量情况下,Bézier提取算子的表达式如下:
C(ζ,η)=Cext(η)⊗Cext(ζ)
(12)
阶次p=2时,图2中任意单元的局部B样条基函数均可映射为图1b中具有空间保持特点的Bernstein基函数。图4所示为图2中单元3的B样条基函数空间与Bernstein基函数空间之间的映射过程。图5所示为B样条基函数空间与相应的Bernstein基函数空间,具体的映射关系表达如下:
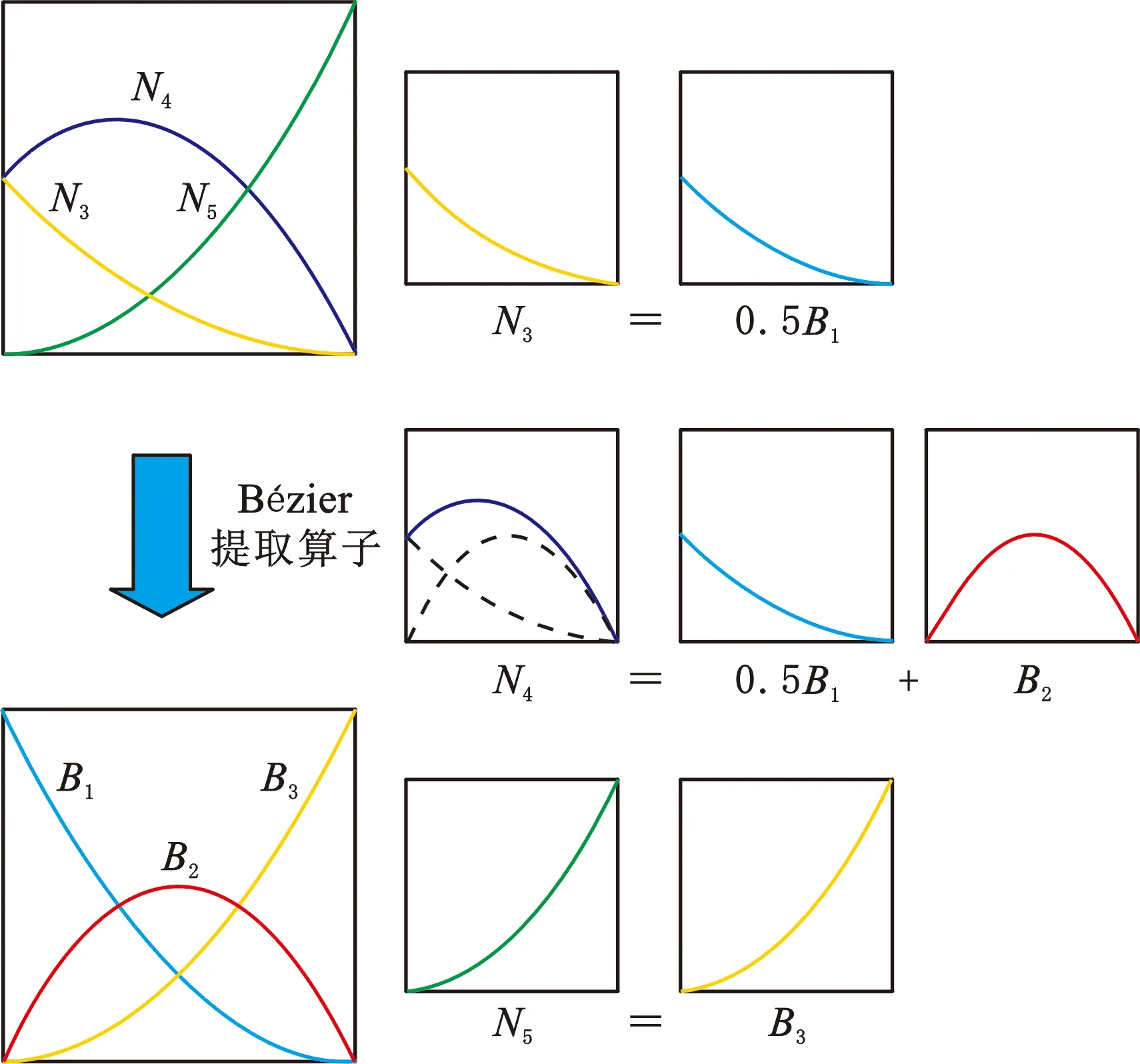
图4 图2中单元3的基函数与图1b的Bernstein基函数的映射关系
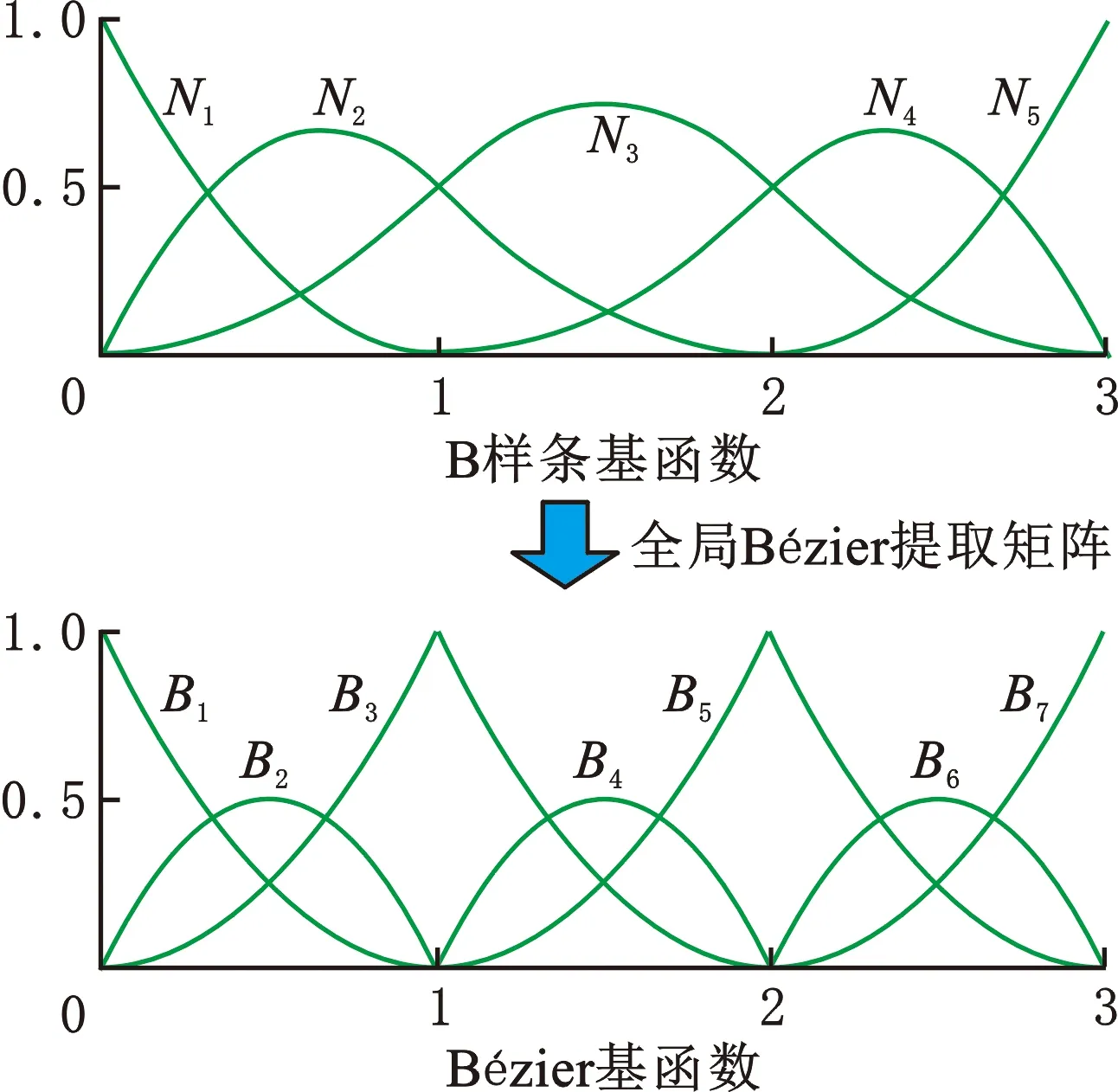
图5 图2中B样条基函数与Bernstein基函数映射关系
(13)
2 多重网格等几何拓扑优化模型
首先介绍B样条空间下等几何拓扑优化模型,在此基础上对传统多重网格等几何拓扑优化模型[23]进行回顾;接着,基于Bézier提取算子对传统等几何拓扑优化模型进行重构,获得改进多重网格模型;最后,通过多重网格各层设计变量之间的映射关系,完成改进多重网格等几何拓扑优化模型的灵敏度分析。
2.1 传统多重网格等几何拓扑优化模型
给定图6所示的二维矩形设计域,等几何拓扑优化的设计目标是在约束条件下寻找最优的材料分布,即寻找具有最小应变能的最优结构,目标函数表示为

图6 B样条空间下的6×2网格的二维悬臂梁设计域
c(x)=fTu(x)
(14)
式中,x为所有B样条单元的相对材料密度分布向量;c(x)为在材料分布x下的模型结构柔度;f为外部力向量;u(x)为各个控制点上的位移向量。
综合SIMP方法,B样条空间下等几何拓扑优化的数学模型可以表示为
(15)
式中,ne为设计域离散成B样条网格的单元个数;xe、ue、Ke(xe)分别为第e个单元的相对密度、位移向量和刚度矩阵;K(x)为全局刚度矩阵;V(x)为固体材料的体积;V0为设计域的总体积;vf为模型限制的材料体积分数;为x的可容许空间。
式(15)中的Ke(xe)可由下式获得:
(16)

Ee(xe)=Emin+(xe)p(E0-Emin)xe∈[0,1]
(17)
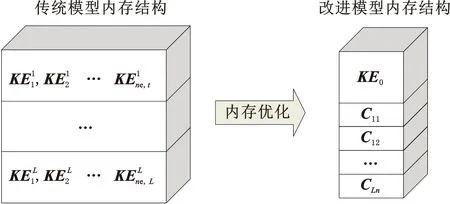
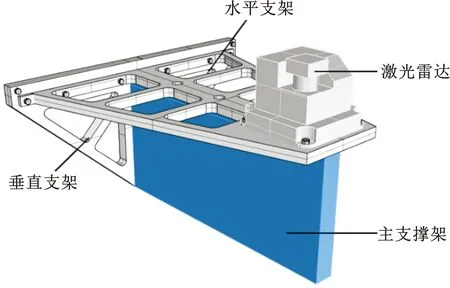
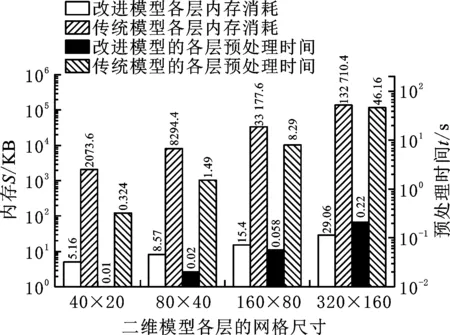
式中,E0为实体材料的弹性模量;Emin为空白单元的弹性模量,通常取0 基于多重网格的等几何拓扑优化模型是一种平衡优化效率与优化精度的有效手段,具体过程为:首先,等几何拓扑优化在较粗的网格下进行优化,此时迭代的速度较快、计算成本较低;然后,当设计变量变化较小时,将粗网格优化结果映射为更细网格的初始设计,并在细网格上进行等几何分析和优化;最后,重复以上操作若干次,由最精细的网格生成等几何拓扑优化结果。 多重网格优化框架如图7所示,其中,等几何拓扑优化部分是基础部分,是迭代过程中的迭代体;设计变量映射继承部分是算法实现的核心,是迭代过程中完成代际继承的关键。本文采用的设计变量映射方法为多维度扩展方法,具体实现过程为:通过Kronecker乘积方法将粗网格模型的优化设计变量以1对4(二维)或8(三维)的方式等值映射至细网格模型,进而实现细网格模型相应设计变量的初始化,如图8所示。通过这样的分层迭代过程与代际映射继承的方式,在保证优化精度的前提下显著提高优化求解的效率。 图7 多重网格等几何拓扑优化的算法流程图 (a)二维多重网格模型映射示意图 将多重网格的框架与式(15)所示的数学模型相结合,得到多重网格等几何拓扑优化模型: (18) 式中,l为多重网格模型的网格层级,l=1,2,…,L;xl的元素取值区间为[0,1]。 首先,基于Bézier提取算子对传统等几何拓扑优化模型进行重构;接着,将改进等几何拓扑优化模型与图7所示的多重网格的框架结合,提出B样条单元刚度矩阵统一表达的多重网格等几何拓扑优化模型。 (19) (20) 式(19)中,Be,Ber是关于Bernstein基函数的偏导数矩阵。根据图5可知,任一B样条单元的基函数均可使用相同的Bernstein基函数空间进行等效表达,即各个单元的Be,Ber均相等。 根据上述特性及式(20),可推导得到图9所示的不同Bézier单元刚度矩阵之间的关系: 图9 Bernstein空间下6×2网格的二维悬臂梁设计域 (21) 通过Bézier提取矩阵,图9所示的B样条单元刚度矩阵表达式如下: (22) 根据等几何分析的等参特性,除了几何空间可使用Bézier提取算子进行映射之外,B样条和Bézier控制点的位移向量也可使用Bézier提取算子实现二者之间的转换。B样条控制点位移u到Bézier控制点的位移ub的转换方程如下: (23) 基于以上的分析推导,对式(15)多重网格等几何拓扑优化模型进行重构,可得 (24) 相对于传统多重网格模型,本文提出的多重网格等几何模型的单元数据存储结构优化如图10所示,其中,L、n分别表示多重网格模型的层数与等几何分析域参数空间的维度,KE0为各层统一的标准单元刚度矩阵。传统的多重网格模型每一层都需要进行所有B样条单元刚度矩阵的计算和存储,而本文多重网格模型采用标准Bézier单元刚度矩阵与相应的Bézier提取算子实现任意层级的任一B样条单元刚度矩阵的统一表达,大幅减少了多重网格等几何拓扑优化的预处理时耗与单元数据内存的消耗。 图10 传统与本文多重网格等几何拓扑优化模型的单元刚度矩阵内存结构对比 根据式(24)的数学模型以及图7所示的算法流程,目标函数相对于第l层的任意一个设计变量xe,l的灵敏度表达如下: (25) 为避免数值不稳定性现象,本文采用灵敏度过滤器修正目标函数的灵敏度公式: (26) (27) 式中,wa,l为第l层的第e个单元与第a个单元之间的权重因子;dist(e,a)表示第a个单元与第e个单元的质心之间的欧氏距离;rmin为由用户定义的过滤器半径。 本文算例中的程序均运行于Windows 10 系统的MATLAB R2021a,所用计算机的配置为Intel(R)Xeon(R)Gold 5102@2.20 GHz的CPU与64 GB内存。图11所示为激光雷达测试平台的支撑结构。对于激光雷达的主支撑结构,可使用拓扑优化方法进行优化设计,主支撑厚度较小时可用二维拓扑优化以简化设计与制造流程,主支撑厚度较大时可使用三维拓扑优化。二维和三维的激光雷达主支撑结构设计模型如图12所示。 图11 激光雷达测试平台 图12a中二维主支撑结构受到右侧上端向下的外力负载,分别在该二维主支撑结构的计算条件下应用传统多重网格模型[23]与基于Bézier提取的改进多重网格模型。其中,等几何网格的初始尺寸为40×20,多重网格的最大层数为4。二维主支撑结构的多重网格等几何拓扑优化结果和优化收敛曲线分别如图13和图14所示,其中,PDOF为自由度,k为迭代次数。从图中可知,传统多重网格等几何模型[23]和所提的改进多重网格等几何模型具有相同的优化收敛过程和优化结果,验证了提出的多重网格B样条单元刚度矩阵统一映射法则在二维优化问题中的正确性。 (a)二维算例模型 图13 二维主支撑结构的传统[23]与改进多重网格模型优化结果对比 图14 二维主支撑结构的传统[23]与改进多重网格模型收敛曲线对比 此外,上述两种多重网格等几何拓扑优化模型的各层刚度矩阵计算内存消耗与预处理时间对比结果如图15所示。由图15可知:在各层刚度矩阵计算的内存消耗上,改进模型较传统模型减少99.76%~99.96%;在各层的刚度矩阵计算的预处理时间上,改进模型较传统模型缩短95.89%~99.62%。因此,对于二维拓扑优化问题,所提出的多重网格刚度映射方法可大幅减少多重网格等几何拓扑优化模型各层等几何单元刚度矩阵的内存消耗与预处理时耗。 图15 二维主支撑结构各层等几何刚度矩阵所需的内存空间与预处理时间对比 当多重网格的最大层数均为4且最大网格尺寸变化时,传统模型与改进模型进行二维主支撑结构优化所需的单元刚度矩阵计算总内存消耗与总预处理时间对比如图16所示。在不同网格尺寸下,改进模型刚度矩阵数据的总体内存消耗较传统模型可减少98.95%~99.48%,总体预处理时间可缩短99.93%~99.96%。相比于传统模型,改进模型在多种多重网格情况下进行二维优化问题求解所需的等几何单元刚度矩阵的总体内存消耗与总预处理时耗均可大幅减少。 图16 二维主支撑结构在不同最大网格尺寸下刚度矩阵计算的总体内存消耗与总预处理时间变化对比 三维主支撑结构算例模型如图12b所示,结构的右上部分受到负载的作用。其中,等几何网格的初始尺寸为40×20×10,多重网格的最大层数为2。三维主支撑结构等几何拓扑优化的优化结果和优化收敛曲线分别如图17和图18所示。从图中可知,传统模型和改进模型具有相同的优化收敛过程和优化结果,验证了提出的多重网格B样条单元刚度矩阵统一映射法则在三维优化问题中的正确性。 图17 三维主支撑结构的传统[23]与改进多重网格等几何拓扑优化模型优化结果对比 图18 三维主支撑结构的传统[23]与改进多重网格模型收敛曲线对比图 上述两种多重网格等几何拓扑优化模型的各层刚度矩阵计算内存消耗与预处理时间对比结果如图19所示。从图19中可知:在各层的刚度矩阵计算的内存消耗上,改进模型较传统模型减少99.97%~99.99%;在各层的刚度矩阵计算的预处理时间上,改进模型较传统模型缩短94.96%~94.99%。因此,对于三维拓扑优化问题,本文提出的多重网格刚度映射方法可大幅减少多重网格等几何拓扑优化模型的各层等几何单元刚度矩阵的内存消耗与预处理时耗。 图19 三维主支撑结构各层等几何刚度矩阵所需的内存空间与预处理时间对比 当多重网格模型的最大层数为2且最大网格尺寸变化时,传统模型与改进模型进行三维主支撑结构优化所需的单元刚度矩阵总内存消耗与总预处理时间对比结果如图20所示。在不同网格尺寸下,改进模型单元刚度所需的总内存消耗较传统模型减少99.98%~99.99%,所需的总体预处理时间缩短94.97%~95.52%。因此,本文改进模型在不同的多重网格情况下进行三维优化问题求解所需的等几何单元刚度矩阵的总体内存消耗与总预处理时间上都较传统模型有明显优势。 图20 三维主支撑结构在不同网格尺寸下刚度矩阵计算的总体内存消耗与总预处理时间变化对比 综合优化模型设计分析与实验结果分析,本文提出的改进多重网格模型具有正确性以及内存和预处理时间方面的高效性,具体表现为:本文方案在优化过程与优化结果上与传统方案保持一致,证明了本文方案是传统方案正确有效的替代方案;二维与三维模型的拓扑优化刚度计算中,改进模型的各层内存消耗与各层预处理时间都较传统模型具有优势;二维与三维模型的拓扑优化刚度计算中,改进模型的总内存消耗与总预处理时间都较传统模型具有优势。 本文提出一种基于Bézier单元刚度映射的改进多重网格等几何拓扑优化模型,解决了传统的多重网格等几何拓扑优化模型刚度矩阵计算过程存在的单元数据存储内存消耗过大和预处理时间过长的问题。通过Bézier提取算子将B样条基函数等效表达为具有空间保持特点的Bernstein基函数,建立了标准Bézier单元刚度矩阵与各层Bézier提取算子进行各层级B样条单元刚度矩阵的统一表达,实现了多重网格等几何拓扑优化内存结构的优化与B样条单元数据预处理过程的简化。在二维和三维拓扑优化问题中,本文提出的模型在数据存储负担与预处理效率上均得到大幅度的改善,进而验证了本文提出的改进多重网格等几何拓扑优化模型的有效性。

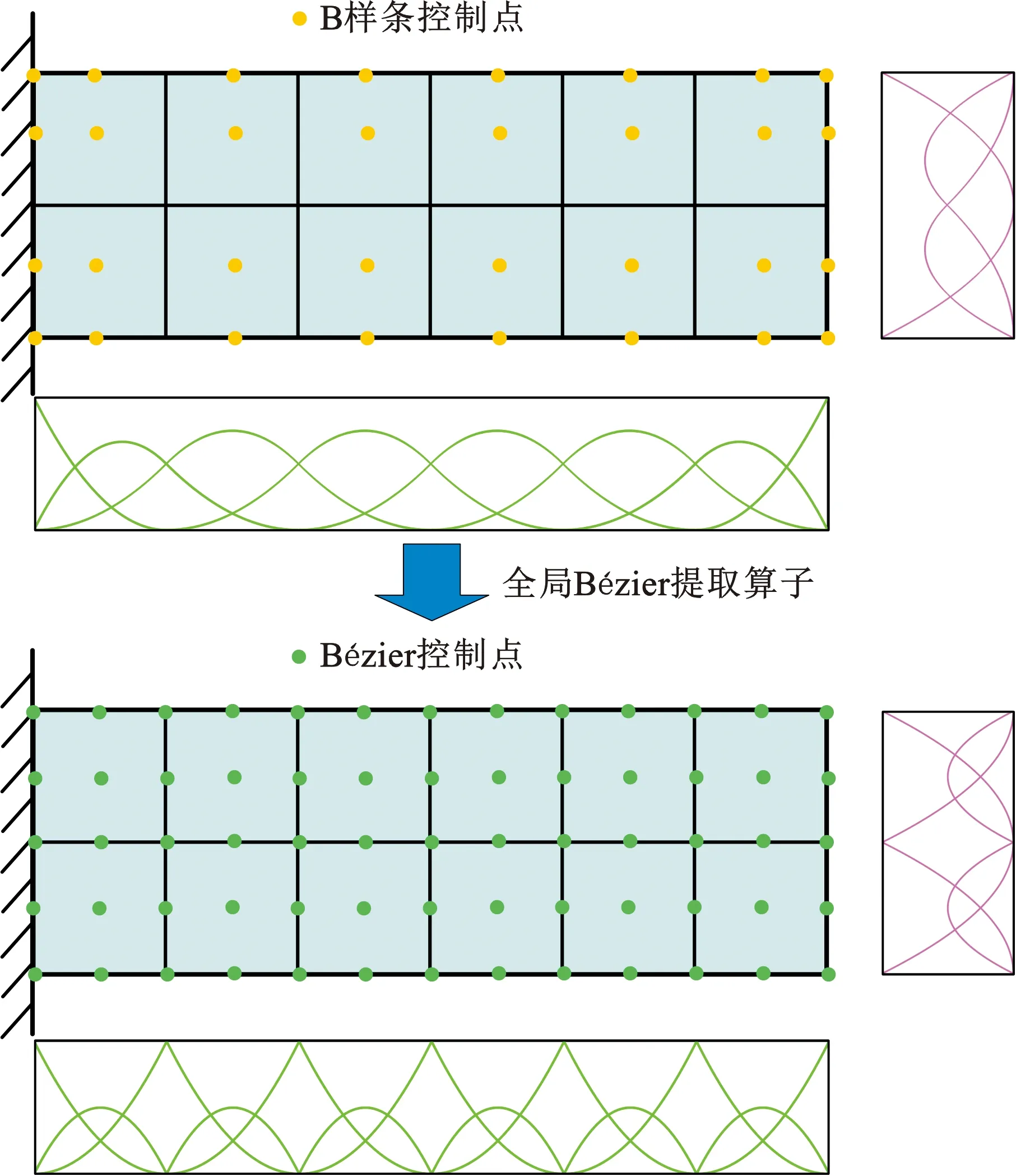
2.2 基于Bézier提取算子的多重网格等几何拓扑优化模型

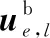
2.3 灵敏度分析
3 数值算例








4 结语

