I-WP型极小曲面空心多孔结构设计与力学性能分析
杜义贤,孙鹏飞,付君健,2+,田启华,2,周祥曼,2,陶 然
(1.三峡大学 机械与动力学院,湖北 宜昌 443002;2.三峡大学 水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443002;3.长江三峡通航管理局,湖北 宜昌 443002)
0 引言
多孔结构具有优越的力学性能[1]和良好的减震及吸能效应[2-3],且结构类型繁多[4-5],其周期性分布的点阵结构可作为新型机械防撞结构的优良载体,在船舶、航天及车辆等领域具有广泛的应用。例如,船舶过闸与闸门发生碰撞将对人员、设备和航道产生巨大的安全威胁,且闸门检修时间长、费用高。因此,设计和安装防撞系统对闸门的安全防护具有重要意义。理想的防撞系统要求防撞结构具有高能量吸收率和一定的承载能力,对结构进行创新性设计可有效满足防撞结构的力学性能需求。
三周期极小曲面是平均曲率为零的曲面,作为新型多孔结构,由特定数学函数描述[5-6],可设计性强,受到国内外研究人员的广泛关注。由于其优良的承载能力、吸能特性[7]、导热性和导电性[8],在多功能承载、抗冲击、热交换、电力传输等领域具有较好的应用前景。增材制造技术的发展解决了多孔结构的制造难题,推动了三周期极小曲面多孔结构性能特性的研究。基于三周期极小曲面的可设计性,采用梯度设计和混合设计,可实现三周期极小曲面多孔结构的创新设计。例如,在三周期极小曲面函数中引入线性函数,可生成梯度多孔结构,相比于均匀多孔结构,具有更优的吸能特性[9]。不同类型三周期极小曲面之间的混合设计,可构成具有新型结构特征的多孔结构。在各向同性属性条件下,混合型三周期极小曲面多孔结构的弹性性能较其单一多孔结构更优[10],且体积模量更逼近Hashin-Shtrikman理论极限[11]。综上可知,梯度设计和混合设计可有效获得新型多孔结构,但梯度设计侧重于提升结构吸能特性,混合设计则侧重于提升多孔结构整体性能。
空心设计属于一种多孔结构的混合设计方法,以多孔结构为基础结构,去除内部材料,得到了空心多孔结构[12],且其压缩和剪切强度优于多孔结构。例如,体积分数为0.3%~5.8%的金字塔空心多孔点阵结构的压缩和剪切强度可达相同体积分数多孔点阵结构的3倍~5倍[13]。对于结构面外压缩强度,空心多孔结构是相同体积分数下多孔结构的两倍以上[14-15]。空心多孔结构的高性能取决于其几何特征,由于其具有大量的细长构件和曲面特征,在受到外压力时,其失效机制转变为屈曲失稳,而结构的屈曲失稳极限取决于其几何构型。相对于相同体积分数的多孔结构,其空心多孔结构的界面惯性矩更大,具有良好的抗屈曲性能[16]。此外,空心多孔结构因内部空间较大,在受到冲击载荷时能吸收更多的能量[9,17]。由以上研究可知,空心设计可有效提升多孔结构的力学性能和吸能特性。
目前,三周期极小曲面多孔结构力学性能的研究侧重于Gyroid型多孔结构,而对其他类型三周期极小曲面多孔结构的研究较少。I-WP型三周期极小曲面多孔结构具有高剪切模量,但其压缩强度相对较低[18],吸能特性研究较少。因此,开展I-WP型三周期极小曲面空心多孔结构设计和力学性能研究,提升其压缩强度和吸能特性,有助于丰富极小曲面多孔结构的力学内涵与工程应用。本文设计了I-WP型空心多孔结构,采用数值均匀化法[19]、有限元法和物理实验方法,研究了空心多孔结构的等效属性、静态力学性能、压缩和吸能特性。
1 I-WP型空心多孔结构设计
本文基于I-WP型极小曲面进行空心多孔结构设计。I-WP型极小曲面属于体心立方结构,呈现出中心收缩,空间上向8个顶点伸出支撑。I-WP型极小曲面具有如下优点:①结构可设计性强,具有较高的比强度[20];②增材制造工艺性好,具备自支撑能力,便于清除粉末。
极小曲面的数学表达式是一种三维隐式水平集函数[18],在I-WP型极小曲面函数中引入水平参数t,可控制I-WP型极小曲面体积分数的变化。
(1)
式中:L为极小曲面单胞的边长,F(x,y,z)为极小曲面数学表达式,x,y,z为高维空间的物理坐标。对于I-WP型极小曲面,-25≤t1≤15,对应体积分数为0~1。
根据水平集函数的定义,可得到极小曲面的实体区域。
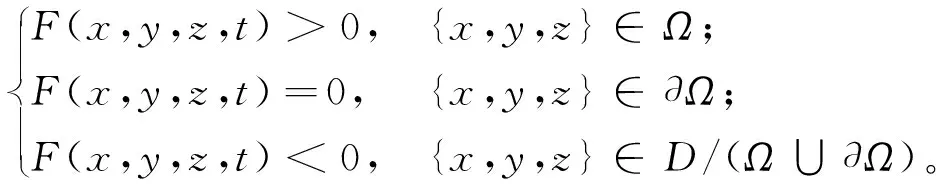
(2)
式中:Ω表示曲面实体区域,∂Ω表示曲面边界,D表示包含实体区域和曲面边界的空间,I-WP型极小曲面多孔结构如图1所示。

为了设计I-WP型空心多孔结构,定义两个I-WP型极小曲面,水平参数分别取t1和t2,得到如图2a和图2b所示的两个极小曲面多孔结构。将两个极小曲面多孔结构作为基础结构,通过差集布尔运算,得到I-WP型空心多孔结构FH的数学表达式。差集布尔运算的数学表达式[21]为式(3),布尔运算过程如图2所示。
FH=min(F(x,y,z,t2),-F(x,y,z,t1))。
(3)
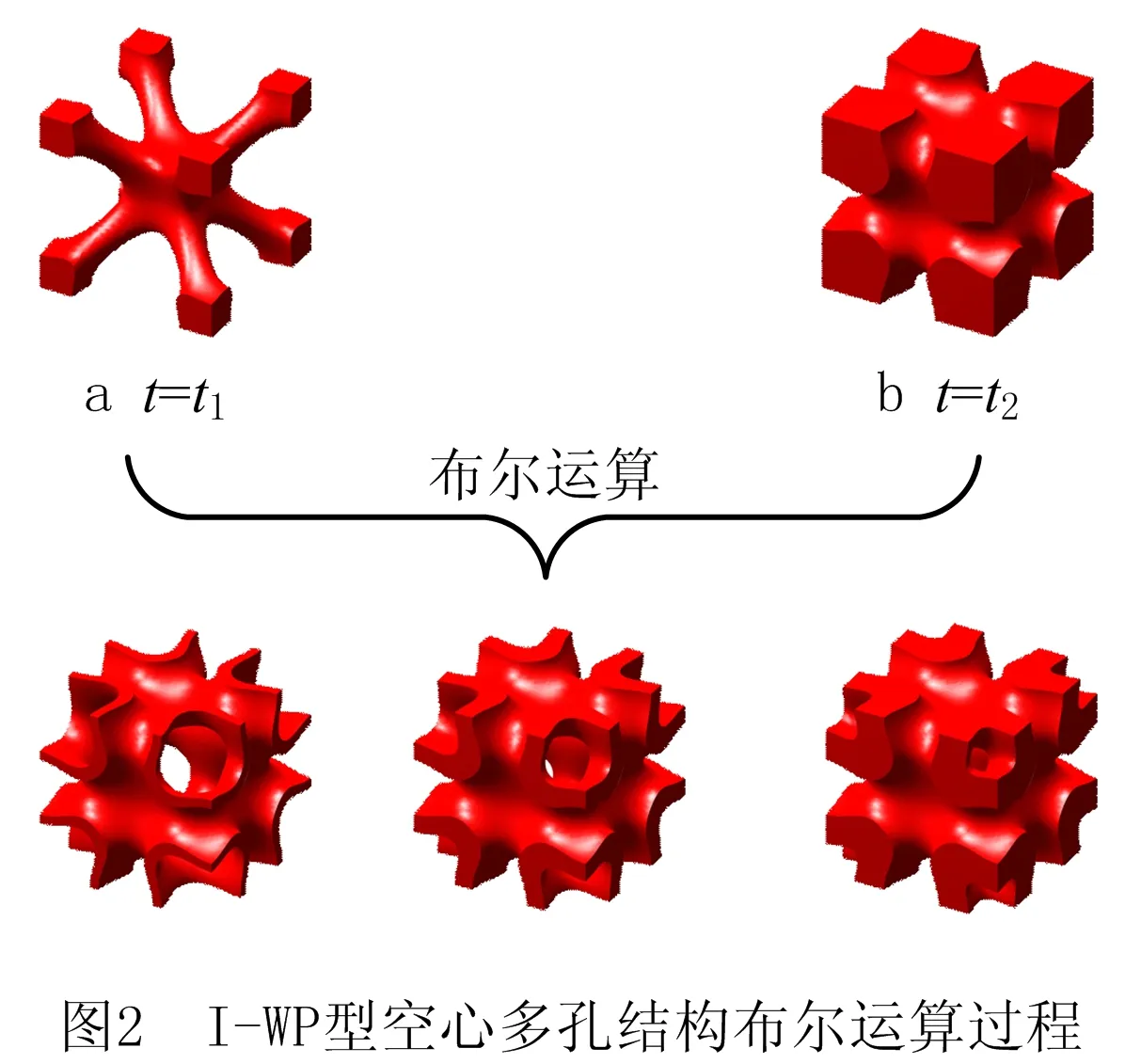
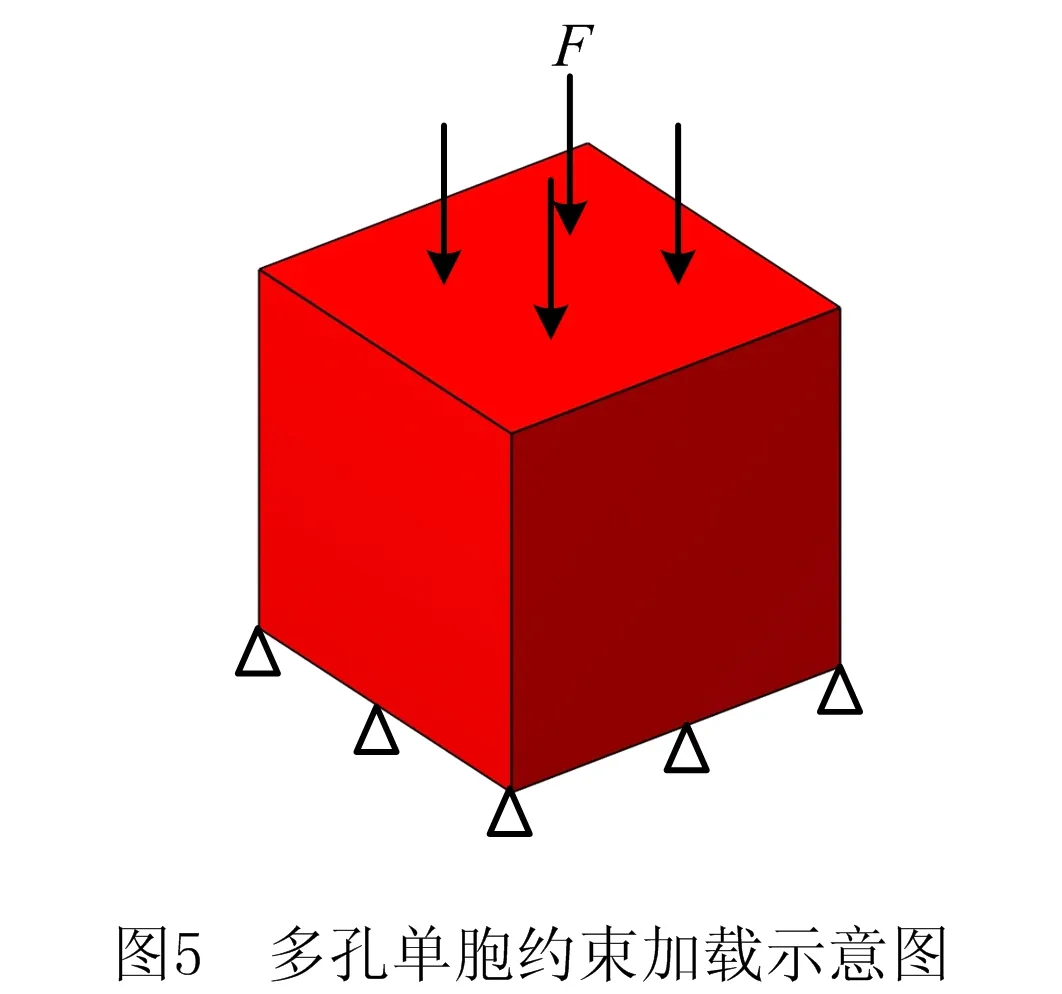
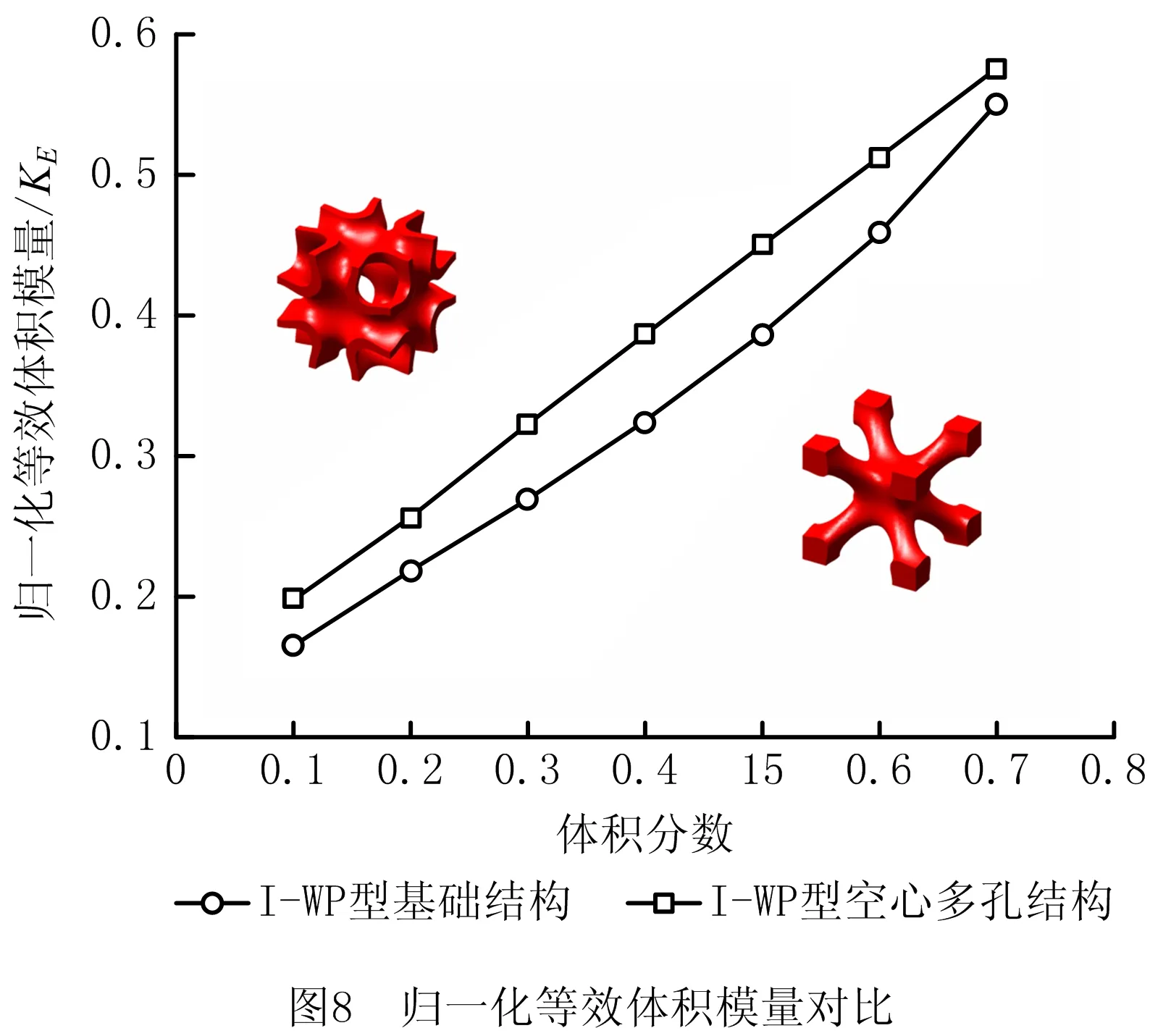
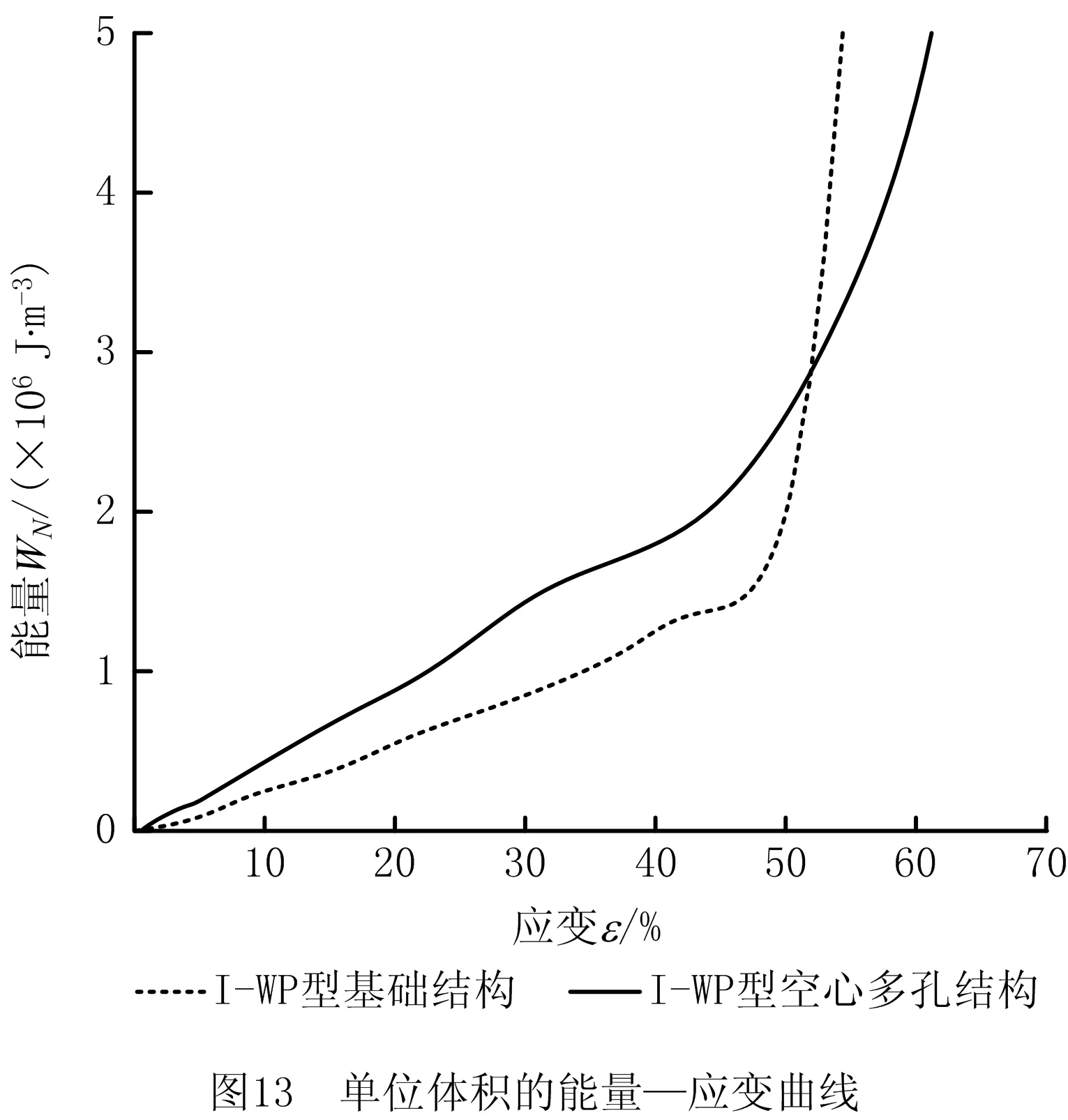
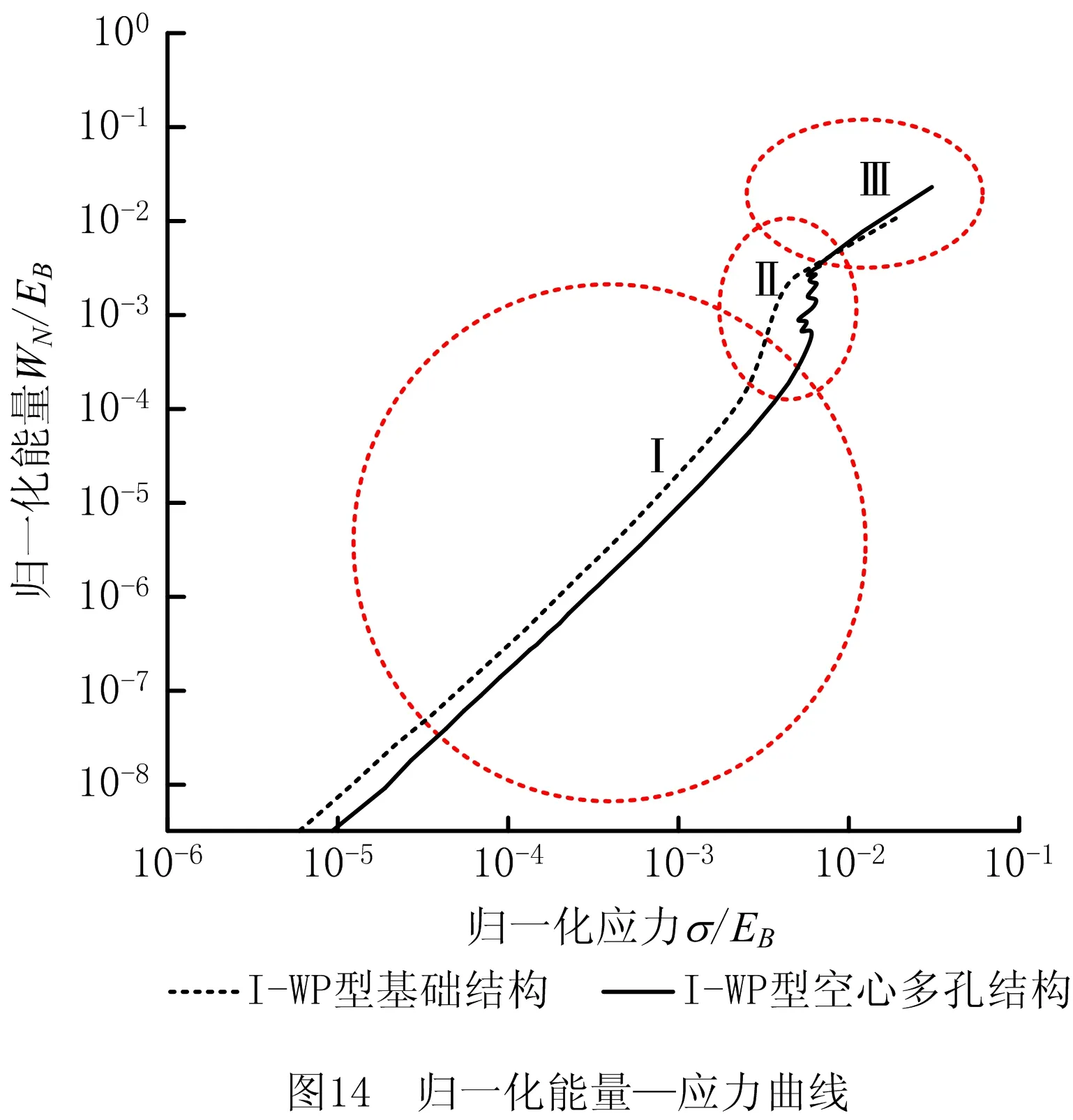
在布尔运算中,令t2 由于极小曲面在空间3个方向上都满足周期性,通过阵列可得到更多周期数量的极小曲面多孔结构,如图4所示为体积分数为0.25的4×4×4均布多孔结构。 为了对比分析I-WP型空心多孔结构与基础结构在线弹性范围内的压缩强度,分别对体积分数为0.25、0.4、0.6,几何尺寸为10 mm×10 mm×10 mm的I-WP型空心单胞和基础结构单胞进行有限元仿真分析。结构材料为PA2200,弹性模量为741 MPa,泊松比为0.3,屈服强度为54 MPa。如图5所示,单胞下表面约束,上表面施加均布载荷,采用四面体单元进行网格划分。 为保证仿真结果的准确性,将多孔结构水平集函数导出为STL模型,对表面进行光滑处理,生成规整的表面网格。每种体积分数的多孔结构进行10组仿真实验,载荷施加方式如下:当体积分数为0.25时,载荷初始值为10 N,每次以10 N递增;当体积分数为0.4时,载荷初始值为50 N,每次以50 N递增;当体积分数为0.6时,载荷初始值为200 N,每次以200 N递增。 体积分数为0.25、0.4和0.6时初始载荷作用下的应变云图如图6所示,由图6可知,I-WP型空心多孔结构的变形更小。图7所示为空心多孔结构和基础结构在体积分数为0.25、0.4和0.6时的应变—载荷图,由图7可知,在线弹性范围内,结构应变与载荷呈线性关系。在相同静态载荷下,I-WP型空心多孔结构的应变值明显小于相同体积分数的基础结构,且I-WP型空心多孔结构的应变—载荷曲线的斜率更小,说明I-WP型空心多孔结构具有更好的抗压缩能力。 数值均匀化法主要用于微观多孔结构的宏观等效性能评估,揭示空心多孔结构的宏观等效力学特性。为进一步说明I-WP型空心多孔结构的性能优势,采用数值均匀化法,计算I-WP型空心多孔结构和基础结构的等效弹性矩阵。 多孔结构等效弹性张量CH的表达式为: (4) 式中:|V|表示单胞的体积,Ve表示单元e的体积,I表示六阶单位矩阵,Be表示单元应变—位移矩阵,χe表示包含单元位移向量,De表示单元本构矩阵。 为求解多孔结构的位移场χ,构建均匀化平衡方程的矩阵形式[21]: Kχ=f。 (5) 其中:全局刚度矩阵 (6) 应变载荷 (7) 其中应变ε中包含6个应变分量:ε11=(1,0,0,0,0,0)T,ε22=(0,1,0,0,0,0)T,ε23=(0,0,1,0,0,0)T,ε12=(0,0,0,1,0,0)T,ε23=(0,0,0,0,1,0)T,ε13=(0,0,0,0,0,1)T。 基于I-WP型极小曲面的高度对称性,其等效弹性矩阵可以简化为: (8) 根据式(9),可以使用等效弹性矩阵中的分量C11和C12来计算等效体积模量 KH=(C11+2C12)/3。 (9) (10) 两种I-WP型曲面结构的归一化等效体积模量对比数据如图8所示。图中数据结果表明,I-WP型空心多孔结构在任意体积分数下的归一化等效体积模量均高于其基础结构。 如图9所示为空心多孔结构和基础结构在不同体积分数下的弹性模量曲面,由曲面形状和数值可知,I-WP型空心多孔结构具有高度对称性,在6个正方向的模量明显高于基础结构。 为分析I-WP空心多孔结构的压缩和吸能特性,进一步验证有限元分析的准确性,选择两种多孔结构进行物理实验。将体积分数为0.25的空心多孔结构和基础结构进行增材制造成型,选EOS-P760型3D打印机,采用选择性激光烧结(Selective Laser Sintering, SLS)[22]技术,PA2200材料,打印了尺寸为40 mm×40 mm×40 mm多孔结构样件。增材制造样件如图10所示,左侧为I-WP型基础结构,右侧为I-WP型空心多孔结构。 选用型号为WDW-100E的微机控制电子式万能试验机,对增材制造样件进行压缩实验。在压缩实验过程中,多孔结构置于实验台,上表面施加5 mm/min的冲击载荷,加载时间为370 s,通过视频记录完整的实验压缩过程。 为分析多孔结构在特定相对密度下的压缩性能,采用Gibson-Ashby模型[23]描述了多孔结构弹性模量、屈服强度、致密化应变与相对密度之间的关系: (11) (12) (13) 式中:ES、ρS和σS分别表示多孔结构的弹性模量、密度和屈服强度;EB、ρB和σB分别表示基体材料的弹性模量、密度和屈服强度;εD表示多孔结构在致密化阶段的初始应变值以及多孔结构实际吸收能量的应变极限值。在达到致密化应变之后,结构将以应力转移为代价继续吸收能量。通过拟合压缩测试结果计算恒定参数C1、C2、n、m和β。 多孔结构单位体积吸收的能量表达式为: (14) 压缩实验过程如图11所示,按应变分为5个阶段:0%、15%、30%、45%和60%。分析压缩过程可知,在发生致密化之前,多孔结构每一层同时发生变形,呈现均匀变化。图12所示为通过实验数据绘制的两种结构的应力—应变曲线,通过分析可得到两种结构的弹性模量、屈服强度、致密化应变和单位体积吸收的能量,具体数值如表1所示。 表1 力学性能和吸能特性参数 表1数据表明,I-WP型空心多孔结构的弹性模量和屈服强度明显高于基础结构,在数值上分别为2.03、1.93倍。I-WP型空心多孔结构开始发生致密化的百分制应变为54.3%,相比其基础结构高6%,说明空心多孔结构具有更长的平台应力期。取n=2、m=3/2[24],基于实验数据,可以得到系数C1、C2和β的值,具体数值如表2所示。根据Gibson-Ashby理论,C1、C2和β的取值范围分别为0.1~4、0.25~0.35和1.4~2.0。由表2中的结果可知,I-WP型空心多孔结构C2的取值超出了Gibson-Ashby理论给出的范围,表明其平台强度高于Gibson-Ashby理论预测的平台强度,因此,相对于其基础结构,空心多孔结构具有更高的平台强度。 表2 Gibson-Ashby系数 多孔结构吸能特性取决于单位体积所吸收的总能量。当结构被压实后,可通过式(14)计算出结构从初始点到开始致密化过程中,单位体积所吸收的总能量,其数值大小即为压缩过程中应力对应变的积分,单位体积的能量—应变曲线如图13所示。由图13可知,在结构发生致密化之前,I-WP型空心多孔结构单位体积吸收的能量—应变曲线的斜率更大,具备更优的吸能特性。 将结构单位体积吸收的能量WN和应力σ对结构弹性模量EB归一化处理,分别得到归一化能量和归一化应力,两者间的数值变化关系如图14所示。将图14中的曲线划分为Ⅰ、Ⅱ和Ⅲ三个阶段,分别对应结构在压缩过程中的线弹性阶段、平台应力阶段和开始致密化至完全压实的阶段。在阶段Ⅰ中,曲线呈现线性变化,能量吸收速度较快,结构处于线弹性范围内;在阶段Ⅱ中,屈服强度出现波动,结构发生破坏,但吸收的能量还在持续增加,结构处于平台应力阶段;在阶段Ⅲ中,结构从开始致密化到被压实,依旧在持续吸收能量,吸收过程出现明显转折,结构应力急剧上升。 本文基于I-WP型三周期极小曲面,采用布尔运算设计了I-WP型空心多孔结构。数值均匀化法和有限元法分析结果表明,I-WP型空心多孔结构较其基础结构具有更高的等效体积模量和更强的静态承载能力。压缩试验揭示了I-WP型空心多孔结构还具有优良的压缩和吸能特性。通过本文研究,提升了I-WP型极小曲面多孔结构的压缩强度和吸能特性,丰富了极小曲面多孔结构力学内涵与防撞领域的工程应用。 考虑到空心极小曲面多孔结构优异的力学性能,未来的研究工作将重点探索极小曲面空心多孔结构的失效机理、几何特征与力学性能间的耦合规律,为防撞领域中多孔结构定制化设计提供借鉴。

2 多孔结构弹性性能分析
2.1 有限元分析


2.2 宏观等效弹性属性分析


3 多孔结构压缩与吸能特性分析
3.1 多孔结构压缩实验

3.2 多孔结构压缩性能分析


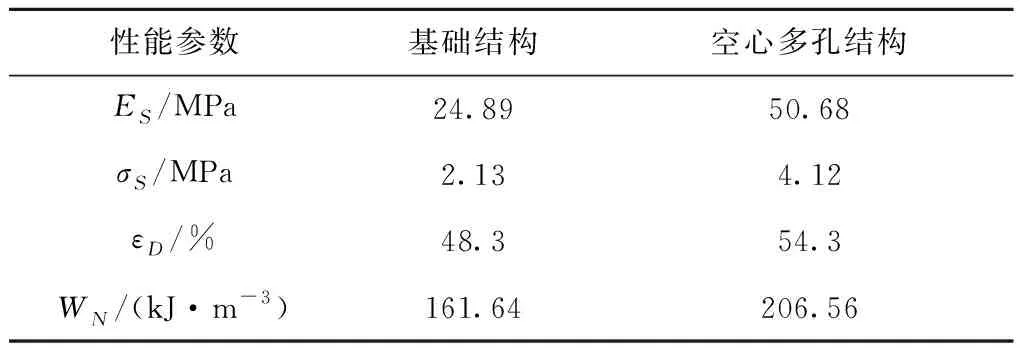
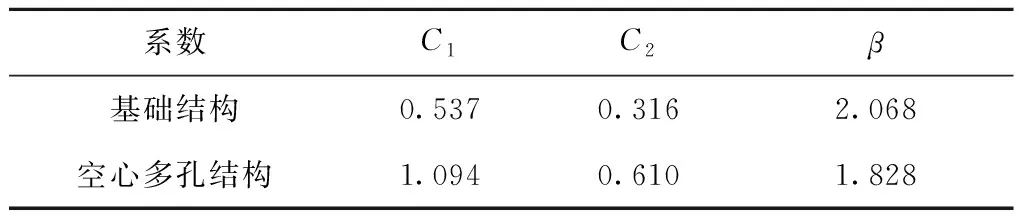
3.3 多孔结构吸能特性分析
4 结束语

