基于能量法的紧固件轴向等效刚度研究及应用
刘晓雪,张亚辉,郭翰飞,谢素明,张有为
(1.大连交通大学 机车车辆工程学院,辽宁 大连 116028;2.大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116021;3.大连交通大学 机械工程学院,辽宁 大连 116028)
0 引言
紧固件作为连接结构中最广泛使用的形式,通常决定着如飞机、动车组等单个复杂组件的设计成败。以动车组为例,单节车体采用数千个紧固件进行各部分的连接,紧固件轴向承载的重要特性是允许非常高的静态强度极限,同等级的紧固件静强度极限为1 000 Mpa时,对应允许的交变应力仅为40~50 Mpa[1]。这意味着当紧固结构受到不同外载荷作用时,需要使用足够精确的刚度来保证紧固件结构的设计准确性。目前,国内外学者对于此类连接的研究主要采用弹性解析模型或数值分析方法[2-6]。当载荷为轴向中心线或微小偏心时,可以采用VDI2230的线性模型;对于载荷作用线偏心较大的情况,需要采用一些非线性模型[7-8];而对更为复杂的载荷作用形式,则需要采用有限元模型,上述分析中均涉及到精确的紧固件及被紧固结构的刚度。紧固结构中各组成部分的刚度可以反映整个结构承受轴向载荷的行为,该载荷主要是指沿紧固件轴线的位移,然而,随着有限元的发展以及研究模型的细致,研究者逐渐认识到原轴向位移假设的求解准确性需要进一步提高[9-11]。LEHNHOFF等[12-14]通过对不同模型进行接触区域节点的等效位移计算来模拟轴向位移,构成紧固件的各个组成部分在轴向载荷作用下的变形规律难以精确地进行计算。MASSOL[10]通过实验对此类计算方法进行了验证,结果证明等效位移计算并不理想。闫平等[15]通过改变紧固结构接触端面的不平行度模拟了累积几何偏差的影响,分析了各种参数对轴向刚度的影响,建立了影响因素与刚度的映射关系,并对刚度组成及变化范围进行了定量分析。WANG等[16]建立了紧固结构相互作用刚度模型,研究了相互作用刚度对预紧力变化的影响,并用有限元模型进行了验证。李国强等[17]对不同型号的紧固件进行了轴向拉伸试验,推导了各组试验的轴向刚度理论公式,并与试验值进行对比,验证了轴向刚度公式的正确性。上述分析中均建立了轴向作用力与轴向位移之间的关系,但是轴向位移的等效计算并不精确。当紧固结构较为复杂时或被紧固结构具有不同尺寸和材料特性的情况下,等效刚度并不容易获得。应变能是结构中伴随变形而产生的能量增量,应变能等于施加在结构上的载荷所做的功,对于承受轴向载荷的紧固件各子结构而言,通过有限元模型可以非常方便地得到其应变能,将各部分同化为具有等效刚度的弹簧元件,从而避免了轴向位移的计算和测量,而位移测量是前述研究中发现的刚度误差主要来源,基于有限元模型采用能量方法进行刚度的计算可以准确且简便地完成分析。
本文基于有限元应变能提出了建立轴向等效刚度特性的方法,避免了轴向位移的等效计算。应用Python进行基于ABAQUS的二次开发,生成参数化模型建模插件,研究并推导了基本参数的拟合函数。在等效参数精确计算的基础上,建立对应的紧固件凝聚单元参数建模插件,并应用于具有大量紧固件结构的组件建模,使有限元模型的建立简单高效。
1 紧固件轴向等效刚度
1.1 紧固件数值模型的校验
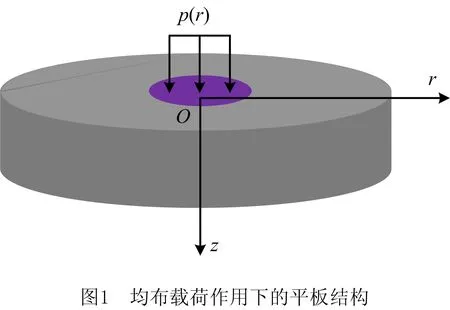
采用紧固件进行两个或多个组件连接的研究主要集中在两个方面:①紧固连接的刚度及其对载荷的响应;②固定界面中接触压力分布的几何形状和大小。目前,国内外学者对于此类连接的研究主要采用弹性解析模型或数值分析方法[1],计算紧固结构的夹紧性能和接头刚度并确定界面压力分布。1964年GREENWOOD[3]在SNEDDON[4]的研究基础上,采用柱坐标(r,θ,z),给出了如图1所示的组件,当作用载荷p(r)的圆形区域半径u变化时,轴向应力σz的解析表达式如式(1),积分上下限涵盖了从无限受压面积到集中载荷的极限情况:
(1)

(2)
式中:ρ=r/h,λ=u/h,a为载荷作用的圆形区域半径。
根据紧固件连接结构的特点,本文采用轴对称模型进行有限元分析。为验证轴对称有限元模型的合理性,并保证应用基于有限元模型能量法的刚度计算准确性,应用2种材料和3种板厚,设计了4个对比模型,模型基本参数如表1所示,定义模型名称为M1~M4。采用ABAQUS软件建立有限元模型,并选取轴对称四边形单元(CAX4R)进行网格划分。

表1 验证模型的基本参数
将式(1)Greenwood的解析表达式计算结果与按表1参数设计的有限元模型的轴向应力计算结果进行对比,结果如图2所示。由图2可知,解析解与M1~M4的有限元分析结果基本吻合,表明了采用轴对称有限元模型进行分析的合理性,也保证了后续应用该轴对称有限元模型进行基于能量法紧固件等效刚度研究的准确性。

1.2 基于能量法的紧固件等效刚度原理
从整体变形能的角度出发,忽略等效位移求解方法中对局部变形的细致性要求,将如图3a所示的紧固件结构等效为如图3b所示的弹簧模型,结合有限元模型进行等效刚度的求解。其中F和δ分别为紧固件轴向力和位移,可以通过作用在有限元模型上各节点的Fi和δi进行加和得到,同时也可以从有限元模型的计算结果中分别提取被紧固件应变能Wf和紧固件应变能Wb。

将紧固件与被紧固件的接触部分由滑移产生的能耗定义为Wfric,在轴向力作用下该部分能耗如式(3)所列:
(3)
整理可得
(4)

(5)
(6)
当β=1时,滑移能耗为0,即紧固件和被紧固件之间无摩擦,根据能量法可以得到等效刚度的表达式:
(7)
(8)

(9)
(10)
其中:
(11)
(12)
将式(6)、式(11)和式(12)代入式(9)和式(10),整理可得:
(13)
(14)
通过紧固结构的有限元模型计算结果可以很方便地提取出F,δ,Wb,Wf,即可由式(13)和式(14)得到紧固结构的等效刚度,该方法不需要进行轴向位移的计算,同时由于有限元对变形能的精确求解,使得刚度计算准确又简单[18]。
1.3 紧固件结构的参数化模型建立
建立包含有大量紧固件结构的复杂组件模型时,将每个紧固件都采用实体单元进行建立,不仅需要耗费大量的建模时间,还需要增加相应的计算成本。结构设计中,通常将紧固件紧固过程中的力学行为等效为弹簧元件的串并联关系,这种表述形式简便且适用于简化分析中不同几何尺寸及材料参数的紧固结构。等效的结构刚度
(15)
式中:Es为子结构的弹性模量,Aeqi为子结构等效的截面积,Leqi为等效长度。
准确模拟等效模型的关键是确定紧固件的等效长度Leq和等效截面积Aeq,对于如图4a所示的模型,对应的等效模型长度和截面积如图4b所示,等效截面积Aeq包含上、下端部紧固件的截面积,分别表示为A0和As,与之对应的等效长度Leq分别为l0+αd和ls+βd,α和β分别对应紧固件上端的修正系数和下端修正系数;等效截面积对应紧固结构的有效作用面积,当等效截面积Aeq为常数时,等效长度Leq为lf+(α+β)d。

紧固结构的几何参数包括:紧固件的规格公称直径d、紧固件上端直径dn、紧固件厚度ln、紧固杆长度lf、被紧固结构的直径dL、被紧固件厚度Lf、中间孔直径dh;材料参数包括:摩擦系数Coefficient of friction、紧固件弹性模量Eb、密度Db、紧固件下端部弹性模量En、密度Dn、被紧固结构弹性模量Ef、密度Df。
在验证了轴对称模型的适用性基础上,为了研究不同参数对等效刚度的影响,假设紧固件下端参数与上端相同,装配紧固件和被紧固结构构建分析模型。应用Python基于ABAQUS进行整个分析过程的参数化脚本文件定义,借助RSG(really simple GUI)构造出紧固结构参数化模型建模的输入界面,如图5所示。参数类型分为几何参数(geometric parameters)、材料参数(material parameters)、载荷及求解模型参数(force and job),通过参数化建模求解并应用能量法得到等效刚度。

2 相关参数对等效模型的影响
基于能量法得到紧固件轴向刚度的前提下,合理建立两个因素等效长度Leq及等效截面积Aeq,即可以准确完成等效模型的简化。本章对两个参数的相关影响因素展开研究,定义无量纲参量并进行公式拟合,为建立等效模型提供基础数据。
2.1 等效模型长度修正系数
引入一个无量纲修正系数γ表征等效长度Leq与紧固件直径d之间的关系,如式(16):
(16)
在应用1.2节中的能量法得到紧固件准确刚度Kb的前提下,即可以开展对γ相关参数的研究。
(1)几何参数的影响
紧固结构自身的几何参数包括上端紧固部分的宽度dn、高度ln和紧固件的厚度lf,引入无量纲参数α,β,ε表征这3个几何参数与公称直径d的关系,可以对标准及非标准紧固件结构进行量化。选取公称直径d分别为M12、M16、M24、M36的紧固件为研究对象,参数取值如表2所示,其中摩擦系数μ=0.4,所有材料均为钢。

表2 几何无量纲参数取值
应用Parametric modeling of fasteners插件建立紧固件的参数化模型并进行求解,基于能量法得到各模型准确的紧固件刚度,进而求解等效修正系数与无量纲参数α,β,ε之间的关系,计算结果如图6所示。

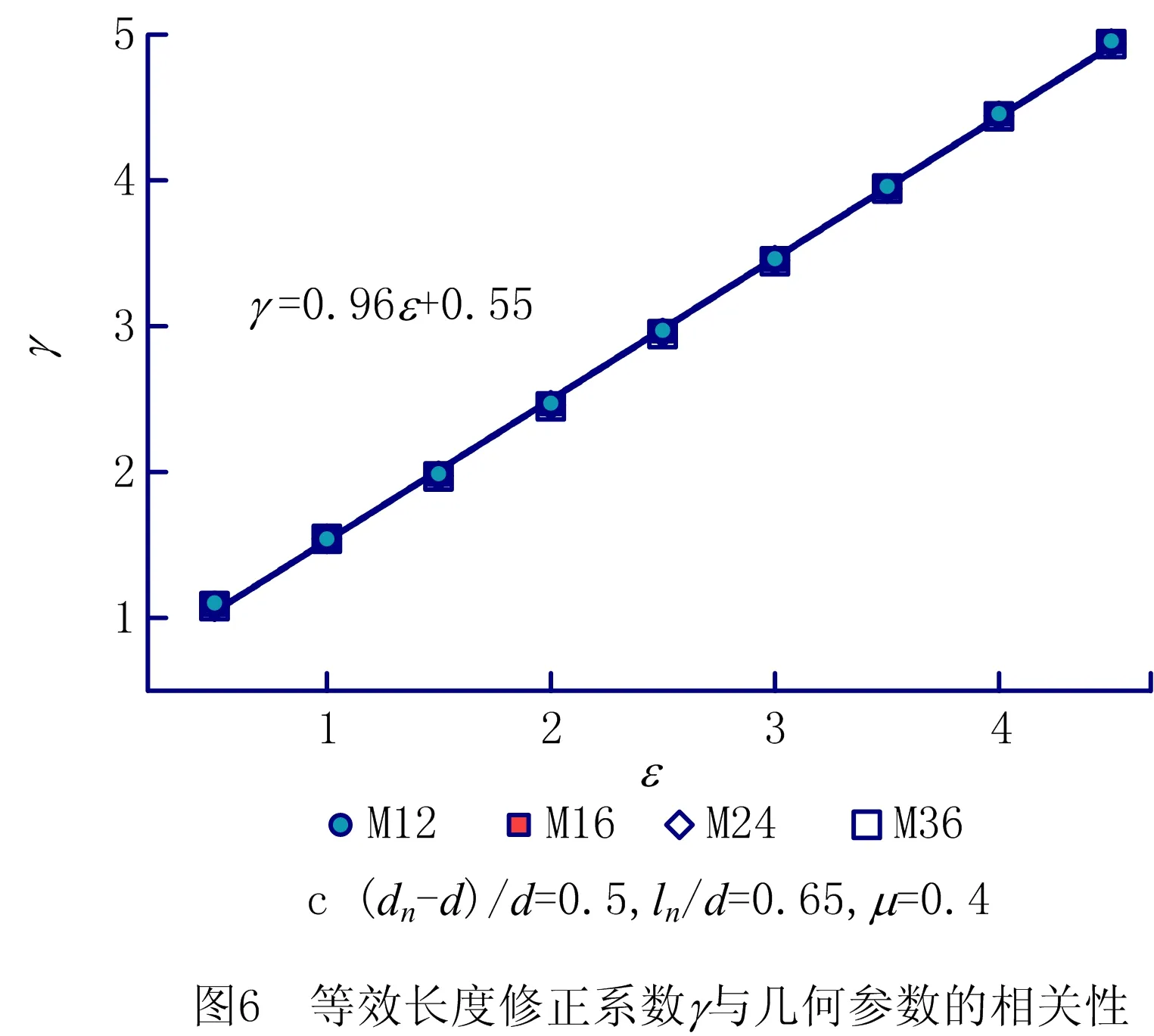
建立等效修正系数γ与几何无量纲参数之间的关系拟合公式:
γα=0.18α+1.9;
(17)
(18)
γε=0.96ε+0.55。
(19)
由图6a和γα拟合公式可得,随着系数α的增大,等效长度的修正系数γ线性增加,α由0.5变化至2.0,等效修正系数变化仅为0.25,表明等效修正系数γ与几何参数上端紧固部dn之间的相关性较低;由图6b和γβ拟合公式可得,当系数β≤0.8时,等效长度的修正系数γ随着β增加而线性减小,当β>0.8时,等效长度的修正系数不再随之变化,等效长度的修正系数与上端紧固部分的高度ln相关性较高;由图6c和γε拟合公式可得,随着系数ε增加,等效长度的修正系数γ呈持续的线性增加,说明等效长度的修正系数与紧固件厚度lf的相关性很高,等效长度的修正系数与3个几何参数的相关性排列规律为ε>β>α。
(2)材料参数的影响
紧固件结构的材料参数包括下端部分弹性模量En与紧固件主体的弹性模量Efastener,引入无量纲参量η和λ分别表征这两个参数与紧固件弹性模量Eb及被紧固件弹性模量E的比值。选取公称直径d分别为M12、M16、M24、M36的紧固件为研究对象,参数取值如表3,几何参数均采用标准件,其中摩擦系数μ=0.4。

表3 结构材料参数取值
应用Parametric modeling of fasteners插件进行紧固件的参数化模型建立及求解,基于能量法得到各模型准确的紧固件刚度,进而求解等效修正系数与无量纲参数η和λ,计算结果如图7所示。

建立等效长度的修正系数γ与材料参数之间的关系拟合公式:
γη=-0.04η+2.0;
(20)
γλ=0.77λ2-3.8λ+5.4。
(21)
由图7a和拟合公式γη可得,随着η的增加,等效长度修正系数γ线性降低,η由0.5增加至3,γη减小了0.1,说明等效长度修正系数γ与下端部紧固结构的材料参数En之间的相关性较低;由图7b和拟合公式γλ可得,随着λ增加,等效长度修正系数γ呈现抛物线型式的下降,λ由0.5增加至3,γλ减小接近4,且变化幅度明显,说明等效长度修正系数γ与被紧固件的材料参数Efastener相关性较高,当2<λ<3,等效长度修正系数γ的变化趋于平缓。
(3)摩擦系数的影响
选取公称直径d分别为M12、M16、M24、M36的紧固件为研究对象,几何参数均采用标准件,所有材料均为钢。假设法向“硬”接触,摩擦系数以0.1为增量变化区间为0~0.4,应用Parametric modeling of fasteners插件进行紧固件的参数化模型建立及求解,基于能量法得到各模型准确的紧固件刚度,进而得到摩擦系数μ与等效长度修正系数γ之间的关系,计算结果如图8所示。

随着摩擦系数μ从0增加至0.4,等效长度修正系数γ的最大变化值仅为0.05,摩擦系数μ=0时的等效长度修正系数与摩擦系数μ=0.4相差4%,该结果与ALKATAN[18]中的计算结果吻合,说明摩擦系数对等效长度修正系数γ的影响可以忽略。
(4)预紧力的影响
选取公称直径d分别为M12、M16、M24、M36的紧固件为研究对象,几何参数均采用标准件,所有材料均为钢。分别施加20%、40%、60%、80%、100%的预紧力,应用Parametric modeling of fasteners插件进行紧固件的参数化模型建立及求解,基于能量法得到各模型准确的紧固件刚度,进而得到预紧力与等效长度修正系数γ之间的关系,计算结果如图9所示。由图9可知,原始尺寸对等效长度修正系数有影响,随着原始尺寸的增加,等效长度修正系数有所减小,但变化范围仅为0.02,而预紧力的变化与等效长度修正系数之间的相关性最大误差为0.8%,说明预紧力对等效长度修正系数γ的影响也可以忽略。

2.2 等效模型修正面积
如图10所示,将紧固结构整体等效为柱状模型时,确定合理的等效修正面积是建立等效模型的关键,基于能量法得到精确的装配紧固结构刚度Kf的基础上可以得到:
(22)


(23)
紧固件连接的其他几何参量也以dn为基准定义相应的无量纲参量:
(24)

(25)
(26)

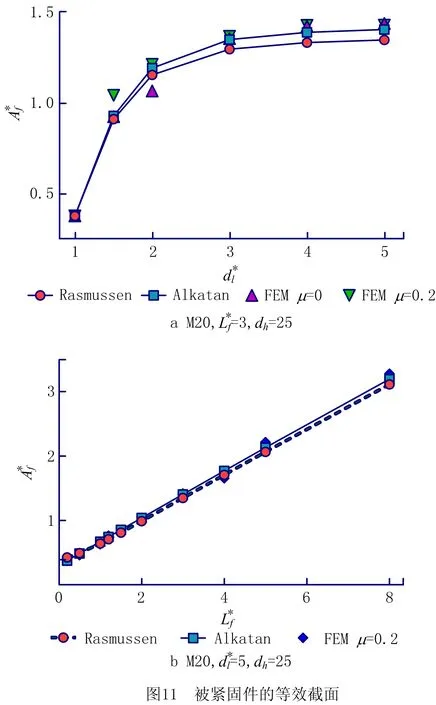
3 等效参数的试验验证
3.1 试验的基本原理
前述研究已证明,预紧力的大小对结构刚度的影响可以忽略,在此前提下,假设外载荷作用大小与紧固件初始结构刚度无关,则可以通过紧固不同弹性模型的结构,分别得到紧固件刚度Kb和被紧固结构刚度Kf。
设计两个几何相同的被紧固件结构,材料分别选择钢和铝,具有弹性模型为Ef1和Ef2,使用完全相同的紧固件进行紧固,弹性模量为Eb,不同外载荷Fi作用下产生相同相对位移δ,
(27)
其中,两种被紧固结构的等效刚度Kfi表示为等效截面Af和等效长度lf的函数:
Kf1=Ef1Af/lf;
(28)
Kf2=Ef2Af/lf。
(29)
当相对位移δ相同时,得到等效面积Af(如式(30))和Kb(如式(31)):
(30)
(31)
测试中下端采用施加扭矩加载的方式,旋转角度Δθ与整体伸长量成正比,只需要确定相同的扭转角θ即可保证两个测试件的相同位移。通过紧固件上应变片的变化量ε得到各扭转角对应的轴向力F,利用式(27)、式(30)和式(31)得到Kb、Kfi的分离刚度值以及影响面积Af,实验和数值计算的基本原理如图12所示。

3.2 验证试验
设计钢制和铝制两种材料的被紧固试件,上部结构厚度为10 mm,下部试件的厚度为12 mm。中心位置为紧固件的安装孔,采用M20的紧固件进行装配,在紧固件端部加工出测试线的开孔以方便测试,如图13所示。

在紧固件杆身的周向对称位置贴两个单向应变片,取其平均值作为轴向力的测试值,在C位置处贴夹角为45°的应变花以测量扭矩,其中单向应变片接1/4惠斯特电桥,应变花接1/2惠斯特电桥,并进行温度补偿,采用东华5922进行数据采集,测试贴片位置及实际布置如图14所示。

3.3 试验验证结果
分别对两组试件施加相同的扭转角度以保证得到相同的伸长量,选取测试值并进行数据采集,得到轴向拉伸的一系列应变结果ε1i和ε2i,对应每个扭转角度取两个应变片应变值的均值作为轴向应变。
(32)
Fi=σmiS=EεmiS。
(33)
其中:S为贴片位置对应的截面积,计算得到相应的轴向力Fi,根据试验原理得到相应的Kb、Kf1、Kf2和Af,同时与前述基于能量法得到的数值结果进行对比,如图15所示。计算m个扭转角度,其中m=6,对应测试值均值与基于能量法求解的结果进行比较,可以得出两者之间的误差,其中Kf1的误差最大为7.89%,Kb的误差最小为2.88%,所有结果均在10%以内,进一步验证了基于能量法轴向等效刚度的准确性。


4 紧固件等效模型的应用
对于包含有大量紧固件结构或者对紧固件选择有要求的结构,合理地应用等效模型建模可以最大限度地简化计算过程,本章在验证了基于能量法的紧固件轴向刚度研究的基础上,将前述等效模型长度及修正面积的研究内容,应用Python结合ABAQUS进行了等效模型参数化建模的插件的开发,如图16所示。在输入紧固件的基本参数后,在Equivalent correction factor插件中选择不同几何参数及材料参数下的等效长度修正系数,从而生成紧固件的等效模型作为子结构模型,在包含有多个紧固结构的组件中可以重复调用,从而减少了建模的复杂性。

选择几何参数β和材料参数η、λ为研究变量,首先应用紧固件等效模型的建模插件Equivalent FM生成不同参数变量的等效模型,以某车下牵引变流器冷却单元吊装结构建立应用数值模型。牵引变流器冷却单元结构外围框架基本尺寸2 700 mm×700 mm×1 430 mm,垂向对应图17中的Y轴,横向对应X轴,纵向对应Z轴,共划分了37 738个节点,43 646个单元,钢制材料,内部为铝合金材质,总重量543.26 kg。
原始模型连接的紧固件采用六面体单元进行划分,采用预紧力单元模拟初始预紧,并在主吊及紧固件之间设置接触关系;等效模型应用Equivalent FM建立不同参数的紧固件等效子模型,生成相应的文件,在主体模型中进行调用,根据标准对两种模型均施加垂向方向1 g加速度的工况,选取框架上端面横向方向中心位置处的垂向位移,验证等效模型的适用性。两种模型对应不同参数变化的对比计算结果如图18所示,由图18a可得,当几何参数β在0.5~2.0之间变化,等效模型与原始模型之间所选取的测试点垂向位移误差最小为1.1%,最大为7.4%;由图18b可得,当材料参数η在0.5~2.0之间变化,该测试点垂向位移误差最小0.5%,最大4.37%;由图18c可得,当材料参数λ在0.5~2.0之

间变化,测点垂向位移最小误差9.17%,最大误差35.4%。参数λ的变化对等效模型的精度影响较大,垂向位移的变化规律与前述研究结果一致。

应用Equivalent FM建立等效模型对于采用多个紧固件进行连接的组件来说具有很好的适用性及准确性。以上述牵引变流器冷却单元的吊装为例,因分析中涉及接触及预紧力加载,单个原始模型的分析时长是采用等效模型的6倍,从计算效率的角度也验证了采用等效模型的合理性。
5 结束语
紧固件及被紧固结构的合理性简化是进行包含此类连接结构动态特性分析的基础,伴随变形产生的能量与有限元法相结合,可以方便快捷地进行此类结构的等效。本文开发了参数化建模工具,从4个主要影响因素进行分析,得出了紧固件的等效长度修正系数公式,同时对被紧固结构等效无量纲截面积进行了两种方法的验证,并确定了合理的等效公式。针对实际结构开发了两种不同材质的双重数值计算,为试验研究提供了方法并对基于能量法计算得到的等效刚度及有效面积进行了验证。应用研究结果基于ABAQUS开发了紧固件等效模型生成插件Equivalent FM,以某车下牵引变流器冷却单元吊装结构为例验证了等效分析的准确性及有效性,为解决此类复杂结构的动态特性分析提供了有效手段。未来在本文研究的基础上,也可以展开针对包含紧固结构动态分析的研究。

