数据污染情形下的全局灵敏度分析
谢 恩,马义中,刘丽君,林成龙
(南京理工大学 经济管理学院,江苏 南京 210094)
0 引言
全局灵敏度分析通常假设试验数据服从正态分布,但数据污染使得实际试验数据偏离假设,伴随着大数据时代海量数据的出现,数据被污染的风险加大[1]。同样,基于污染数据的仿真试验可能会歪曲事物本来的面目,降低说服力,甚至可能得出谬误的结论。因此,如何改进统计方法,使得在面对数据污染时仍能够得到稳健的结果,成为近年来研究的热点问题[2-3]。样本中存在异常值被认为是数据污染的一种,传统的异常值检验技术[4]通过识别异常值并直接舍弃的处理方法,往往导致表示过程质量特性的重要信息丢失,影响后续工作[5]。RIPLEY[6]指出在多元或高维数据情形下难以识别数据中的异常值,需要采用稳健统计方法来抵抗污染值的干扰。
基于稳健模型和稳健统计技术建立模型并估计模型参数,能更好地描述数据集中大多数数据的统计特性,能抵御异常值对仿真试验的影响[7]。SERFLING[8]指出样本数据存在污染的情形时,用中位数和中位数绝对偏差(Median Absolute Deviation, MAD)代替均值和方差估计样本位置和尺度参数可以获得稳健性较高的结果。韩云霞等[9]研究了基于稳健统计量(Hodges-Lehmann, HL)和Shamos估计数据污染情形下最优参数置信区间,结果表明,基于稳健统计量的方法估计精度更高,同时能够抵抗污染值的干扰。PARK等[10]研究了数据污染情形下不同的稳健统计量估计位置参数和尺度参数,通过分析蒙特卡洛仿真试验结果,给出几种稳健统计量在数据污染情形下的有效性,其中分别用HL和Shamos估计位置参数和尺度参数进行稳健设计的最优解优于其他稳健统计量。刘丽君等[11-12]用中位数估计位置参数,用MAD估计尺度参数,改进了序贯分支试验的显著性检验程序,在不增加额外试验次数的前提下,解决了不同类型数据污染情形下的因子筛选问题。
灵敏度分析方法主要分为3类[13-14]:①旨在区分模型输入因子是否对模型输出有影响的因子筛选方法(screening method);②局部灵敏度分析方法(local sensitivity analysis),考虑围绕特定设计点的微小扰动对模型输出不确定性影响;③全局灵敏度分析方法(global sensitivity analysis),考虑整个输入空间内的因子变化对模型输出不确定性的影响,旨在对模型所有输入因子基于其对模型输出不确定效应的贡献进行重要度排序。Sobol’指数法作为基于方差的全局灵敏度分析方法[15-16],独立于模型输入和输出,容易解释和实现,适用于模型输入因子排序和重要变量筛选,在工业工程、环境和大气工程及化工工程等领域被广泛研究和使用[17-19]。但在面对复杂问题时,Sobol’指数通过大量的模型估计也很难得到收敛的合理解,无法识别因子重要度。随着计算机技术的发展和进步,使得几乎所有工程领域复杂系统的行为都能用数值模型来模拟和预测[20],因此,基于代理模型的全局灵敏度分析方法获得了高度关注[20-22]。另一方面,基于方差的Sobol’指数蒙特卡洛仿真计算技术也得到了改进[23-25],双循环重排序方法(Double Loop Reordering approach, DLR)作为Sobol’蒙特卡洛仿真技术改进方法的一种,使得仿真计算效率得到很大的提高[26-29]。
然而,在数据存在污染的情形下,不能准确反映样本的统计特性,导致基于方差的灵敏度分析方法无法识别因子重要度或对因子重要度进行排序,无法正确度量模型输出不确定性的来源,从而使得模型更加复杂、计算成本更高。针对仿真试验中数据污染(本文指数据中存在异常值)的问题,引入稳健统计量改进Sobol’法中的DLR蒙特卡洛仿真方法,提出了稳健双循环重排序方法(Robust Double Loop Reordering approach, RDLR),并通过仿真试验验证了所提方法的有效性和稳健性。
1 稳健统计量及其性质
1.1 稳健统计量及其相对效率


1.2 两组稳健统计量的渐近分布特性
基于稳健统计量HL-Shamos组合,可构造如下统计量[30]:
(1)
基于稳健统计量Med-MAD组合,可构造如下统计量[33]:
(2)
为了验证两组稳健统计量的分布情况,在正态分布假设条件下,分别在样本量(n)为10和100时进行1 000次随机抽样,基于样本点绘制统计量TMM,THS的正态分布QQ图,以及样本量为10的经验累计分布图和概率密度函数图如图1所示。

对比图1a和图1b可知,在样本量较大时,两组统计量更趋向于正态分布;在样本量较小时,基于统计量THS的分布更趋向于正态分布。如图1c所示为基于统计量THS、TMM以及均值—方差的经验累计分布图,如图1d所示为基于统计量THS、TMM以及均值—方差的密度函数,分析图1c和图1d可得,统计量THS、TMM的分布均近似服从正态分布,且基于统计量THS的分布更接近正态分布。因此,在样本量较小时建议优先选择THS统计量。基于稳健统计量的渐近正态分布特性,本文采用稳健统计量代替均值和标准差估计样本的位置参数和尺度参数是合理的。
2 基于稳健统计量的全局灵敏度分析
2.1 稳健统计量替代均值和方差的全局灵敏度分析
假设系统某一质量特性Y和m个可控输入变量x=(x1,…,xm)之间的关系为Y=f(x),则模型输出的全方差公式为:
V[Y]=Vxi[Ex-i[Y|xi]]+Exi[Vx-i[Y|xi]]。
其中:E[·]表示期望,V[·]表示方差,x-i表示除xi之外的输入因子,Vxi[Ex-i[Y|xi]]用来定量地度量输入因子xi对模型输出的影响。因此,因子xi基于方差的一阶全局灵敏度指数计算如下:
Si=Vxi[Ex-i[Y|xi]]/V[Y]。
当模型输出中含有异常值时,考虑采用稳健统计量HL-Shamos或者Med-MAD替代均值—方差计算全局灵敏度指数,使得基于稳健统计量的全局灵敏度分析方法在面对数据污染时仍能准确识别模型输入因子的重要度。

其中:a=1.158 75;a1=0.414 253 297;a2=0.442 396 799;当n≤100时,a3=a4=0,当n>100时,a3=2.822,a4=12.238。
其中:b=2.702 7;b1=-0.762 13;b2=-0.864 13;当n≤100时,b3=b4=0,当n>100,且n为奇数时,b3=0.299 6,b4=-149.357,当n为偶数时,b3=-2.417,b4=-153.01。
基于稳健的位置参数—尺度参数为HL-Shamos组合的全局灵敏度指数定义为Si1,i2,…,ik(HS),
Si1,i2,…,ik(HS)=
(3)
基于稳健的位置参数—尺度参数为Med-MAD组合的全局灵敏度指数定义为Si1,i2,…,ik(MM),
Si1,i2,…,ik(MM)=
(4)
式(3)和式(4)中{i1,i2,…,ik}是{1,2,…,m}的一个子集,且1≤i1<… 假设函数f在积分空间Im=[0,1]m上平方可积,函数f通过Sobol’分解可分解为: fi,j(xi,xj)+…+f1,2,…,m(x1,x2,…,xm)。 当文献[15]中的条件满足时,上式的分解是唯一的,对其两边平方并积分,可得: 假定两互补子集y和z构成输入变量x=(y,z),令子集y=(xi1,xi2,…,xik),子集y的方差 Sobol’法的总方差为 其中{i1,i2,…,ik}是{1,2,…,m}的一个子集,即1≤i1<… 在仿真试验中,假定x和x′是样本空间中两个N×m维相互独立的抽样数组,令x=(y,z),x′=(y′,z′),对应于输入因子子集y=(xi1,…,xik)的方差为: 针对样本均值和方差对异常值敏感的问题,提出稳健双循环重排序方法(RDLR),采用稳健统计量替代均值—方差改进传统的DLR方法。用稳健的位置统计量估计每个分区中Nm个模型输出的位置参数,即对第k(1≤k≤M)个分区分别计算HL统计量和中位数Med统计量来估计每个分区中模型条件输出的位置参数,形式如下: p,q=1,…,Nm,k=1,…,M; 由上式可得M个稳健的条件输出位置统计量,然后用稳健的尺度参数统计量Shamos和MAD估计M个位置参数统计量的稳健尺度参数: (5) (6) 模型非条件输出的稳健尺度参数为: f(yq,zq)|))2/A(N),p,q=1,…,N; (7) (8) 因此,由式(5)~式(8)可得,输入变量y=xi的基于稳健统计量改进的RDLR方法的一阶全局灵敏度指数,即一阶Sobol’指数的计算公式为: Sy(HS)=Dy(HS)/DHS; (9) Sy(MM)=Dy(MM)/DMM。 (10) 基于稳健统计量的RDLR方法具有较高的稳健性,能够抵御异常值的影响,其仿真算法实现步骤如下: 步骤1算法初始化(测试函数选择),随机生成N个m维的样本点xj,计算对应的输出f(xj)。 步骤2令y=xi(1≤i≤m)获得排序后的样本点x(j),j=1,2,…,N,将排序后的输入变量对应的输出f(xj)分成M(M 步骤4计算所有样本点xj对应的非条件输出的稳健尺度参数DHS和DMM。 步骤5计算基于稳健统计量的输入因子灵敏度指数Dy(HS)/DHS和Dy(MM)/DMM。 步骤6重复步骤2~步骤5,令y取每一个输入变量,计算所有输入变量的稳健灵敏度指数。 传统的DLR和改进的RDLR方法能计算单个输入变量的灵敏度指数,对变量子组无效。 为了更好地说明所提方法的有效性,选用3个测试函数对提出的RDLR方法进行验证。Ishigami函数和Sobol G—函数都是全局灵敏度分析研究中广泛采用的测试函数。Ishigami函数具有输入变量间相互关系复杂,能够代表大多数模型输入变量间关系类型的特点[34];Sobol G—函数输入变量数目可变,并且可以通过调节函数表达式中非负常数,进而达到改变模型输入变量的灵敏度指数的目的,具有较高的灵活性[35]。基于方差的方法无法识别非线性偏态分布输出函数的输入变量的重要度[36],为了验证本文基于稳健统计量的方法针对非正态问题的有效性,选择该二维输入的非线性偏态分布输出函数。 考虑数据污染对基于方差的全局灵敏度分析方法的影响,人为增加一个初始输出的污染函数,记为fcon(y,λ),污染后的模型输出为:fcon(y,λ)=y+m·s·I(y),数据污染的相关函数λ=(p,m,s)与3个参数有关,其中p表示样本数据中变异数据的概率,本文取值分别为0(不含异常值)、0.05和0.1,此处给定污染数据占比均小于各统计量的失效点;m表示变异量,取值分别为100和300;s表示变异符号,取值为1和-1;其中I(y)为示性函数,即I(y≥0)=1,I(y<0)=-1。基于各给定变异函数污染参数的取值,可得9种污染参数组合,分别命名为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ和Ⅸ,第Ⅰ种变异概率为0,污染参数组合为(0,-,-),模型输出无污染,不同污染情形的参数组合如表1所示。 表1 不同数据污染情形的参数组合 Ishigami函数[34]包含3个输入因子,表达式为: f(x1,x2,x3)=sinx1+a·sin2x2+ 其总方差D和条件方差D1,D2,D3的理论计算值如下所示: 令a=7,b=0.1,Ishigami函数基于方差的输入因子x1,x2,x3的全局灵敏度指数解析解分别为:S1=0.313 8,S2=0.442 4,S3=0,因此S2>S1>S3,即因子x2重要度为第一,因子x1重要度为第二,因子x3重要度为第三。 如图2所示为Ishigami函数1 000次仿真试验输出在9种不同的污染参数组合情形的均值、HL、中位数、标准差、Shamos和MAD等6个统计量的条形图。 如图2a所示为不同的位置参数统计量的条形图,对比分析可知样本均值对异常值非常敏感,而HL和中位数几乎不受异常值影响;图2b所示为不同尺度参数统计量的条形图,其中标准差受到异常值的影响最大,稳健尺度统计量Shamos和MAD受异常值影响较小。因此,面对数据污染问题,基于稳健统计量的仿真试验结果不易受异常值干扰。 如表2所示为Ishigami函数输出在9组污染情形下的不同统计量的方差,受异常值影响,9组输出的均值和标准差的方差远远大于稳健统计量的方差,即均值和标准差对异常值更加敏感。 表2 Ishigami函数输出在9种污染参数情形下不同统计量的方差 为验证数据污染情形下基于稳健统计量的全局灵敏度分析方法的有效性和稳健性,本试验分别在9种不同污染参数组合情形下各进行1 000次独立重复试验,得到因子灵敏度指数。在每种污染参数组合条件下、每次独立试验中,在模型输入空间中随机抽取1 000个样本点,计算得到1 000个输出,执行一次灵敏度指数计算,得到一组灵敏度指数。Ishigami函数输入因子灵敏度指数基于方差、HL/Shamos和Med/MAD等方法在不同污染情形下,试验所得灵敏度指数的均值统计结果如表3所示。 由表3可知,基于方差的全局灵敏度分析方法,仅在第I种污染参数组合,即输出无污染的情形下能识别因子的重要度;在输出受到污染的情形下,因子x1的灵敏度指数S1和因子x2的灵敏度指数S2几乎相等,无法识别输入因子重要度。基于HL/Shamos和Med/MAD的全局灵敏度指数在9种污染参数组合情形下,都能识别输入因子的重要度,可得输入因子灵敏度指数关系为S2>S1>S3,与解析解的结果一致;对比基于两组不同稳健统计量的因子灵敏度指数仿真试验结果,基于HL/Shamos方法的性能更优,各因子灵敏度指数更接近解析解。 表3 基于不同统计量的Ishigami函数在不同污染情形下因子灵敏度指数 如图3所示为9种污染情形下,Ishigami函数基于不同统计量各进行1 000次独立重复试验的因子灵敏度指数箱线图。由图3a可知,基于方差的方法在数据污染的情形下,不能有效识别因子重要度,基于方差方法对异常值敏感,仿真试验结果受到异常值影响。图3b和图3c分别为基于稳健统计量HL/Shamos和Med/MAD方法的灵敏度指数箱线图,结果表明:在9种污染情形下基于稳健统计量的全局灵敏度分析方法都能正确识别因子重要度,因子灵敏度指数关系为S2>S1>S3,与解析解的结果一致。因此,基于稳健统计量的灵敏度指数计算方法能够实现数据污染情形下因子重要度排序,相比基于方差的方法更稳健。比较图3b与图3c中第Ⅰ种污染参数组合情况可知在输出无污染时,基于稳健统计量的全局灵敏度分析方法同样能够正确识别输入因子的重要度。 样本量较小时,由于统计量THS相对于统计量TMM的分布更趋向正态分布,且统计量HL/Shamos相对统计量Med/MAD的效率更高,因此基于统计量HL/Shamos的全局灵敏度分析方法性能更优。 输出高度偏态分布的函数[36]: y=x1/x2,x1~χ2(10),x2~χ2(13.978)。 输入变量x1对函数输出的贡献比x2对函数输出的贡献大,然而基于方差的全局灵敏度分析方法无法识别出两因子的重要度。 为了验证输出偏态分布且受到污染情形下基于方差、HL/Shamos和Med/MAD等方法的有效性和稳健性,采用与3.1节相同的试验程序,计算9种污染情形下基于不同统计量的输入因子灵敏度指数。在显著水平为0.05时,对9种污染条件下基于方差方法的两因子1 000次仿真试验的灵敏度指数进行检验。结果显示,除第I种污染参数组合外,其它污染参数组合下的P值都大于显著水平,因此两因子1 000次仿真试验的灵敏度指数无显著差异,不能对输入因子进行重要度排序,t检验P值如表4所示。 表4 不同污染情形下基于方差方法的因子灵敏度指数检验 如表5所示为输出偏态分布的函数在9种污染情形下基于不同统计量的全局灵敏度分析方法,各进行1 000次独立重复试验,所得因子的灵敏度指数均值统计结果。由表5可知,在函数输出偏态分布或被污染情形时,基于方差全局灵敏度分析方法无法识别因子重要度,即因子x1的灵敏度指数S1和因子x2的灵敏度指数S2的关系为S1≈S2。对比基于稳健统计量HL/Shamos和Med/MAD方法的灵敏度指数可知,因子x1的灵敏度指数S1显著大于因子x2的灵敏度指数S2,因此基于稳健统计量的灵敏度分析方法不受数据污染或偏态分布的影响,能正确识别因子重要度,具有较高的稳健性。 表5 不同污染情形下基于不同统计量的因子灵敏度指数 如图4所示为输出偏态分布的函数在9种不同污染情形下,基于不同的统计量的全局灵敏度分析方法,各进行1 000次独立重复试验,所得因子灵敏度指数的箱线图。 由图4a可知,在函数输出呈偏态分布条件下,不论输出是否存在污染的情形,基于方差的方法均无法识别因子的重要度,仿真试验结果无法对因子重要度排序;图4b和图4c是基于稳健统计量的灵敏度指数箱线图,结果显示函数输出在9种污染情形下,输入因子x1的全局灵敏度指数S1显著大于输入因子x2的全局灵敏度指数S2,因此基于稳健统计量的全局灵敏度分析方法在数据偏态分布情形下,不论数据是否被污染都能准确识别输入因子的重要度;基于稳健统计量的全局灵敏度分析具有较高的稳健性和更广泛的适用性。 在较高维输入和较高污染数据比例情形下,为了验证本文基于稳健统计量的全局灵敏度分析方法的有效性,选用全局灵敏度分析中常用的测试函数Sobol G—函数[35],其形式为: 其中:输入因子xi(i=1,2,…,d)在[-1,1]d上均匀分布,ai是非负常数。Sobol G—函数可以通过控制非负常数来调节每一个输入对输入方差的贡献。当非负常数ai小时,其对应的输入因子对输出的方差贡献就更大;当非负常数ai大时,其对应的输入因子对输出的方差贡献就小。本文设置输入因子数目为6,每个输入因子对应的非负常数是(a1,a2,a3,a4,a5,a6)=(15,3,2,1,0.1,0),模型输出的污染参数组合如表6所示。 表6 Sobol G—函数的输出污染参数组合 考虑稳健统计量HL和Shamos的极限BP点为29.3%,在此验证数据中污染数据占比较高的情形下,基于稳健统计量的全局灵敏度方法的有效性,设置污染参数最大比例为25%。如表7所示为不同污染情形下6维Sobol G—函数基于不同统计量的1 000次仿真试验所得输入变量灵敏度指数均值统计结果。 表7 不同污染情形下Sobol G—函数基于不同统计量的因子灵敏度指数 由表7可知,基于方差的方法仅在数据不存在污染的情形下能够正确地对输入因子重要度进行排序,再次验证了基于方差的全局灵敏度分析方法不适用于数据污染的情形。基于稳健统计量的方法既能在数据无污染情形下识别因子重要度,又能在数据存在污染的情形下正确地识别因子的重要度。当数据中污染值的比例达到25%时,基于稳健统计量Med/MAD的方法优于基于稳健统计量HL/Shamos的方法,可能的原因是稳健统计量Med/Mad的BP点较高,而25%的污染值的占比使得稳健统计量HL/Shamos的性能较低。 针对数据污染情形下基于方差的全局灵敏度分析方法不能正确识别模型输入因子重要度的问题。本文提出一种新的Sobol’指数蒙特卡洛仿真计算方法RDLR法。通过蒙特卡洛仿真计算两个测试函数在不同的污染情形下基于不同方法的因子灵敏度指数,对比传统的DLR方法和本文所提方法的稳健性和有效性。分析试验结果可得出以下结论: (1)本文所提方法具有良好的稳健性,在模型输出存在异常值时,能正确识别因子重要度,有效抵御异常值的影响; (2)RDLR法具有广泛的适用性,在模型输出理想无污染或高度非正态分布的情形下,能正确识别因子重要度; (3)RDLR方法不必增加仿真试验次数,保证仿真试验的经济性; (4)在模型输入因子数目较小时,基于稳健统计量HL/Shamos的方法性能更优,当数据中污染数据占比较高的情形下,基于稳健统计量HL/Shamos的方法性能更优。 本文主要贡献是通过引入稳健统计量改进了Sobol’蒙特卡洛仿真计算方法,进而提高了其抗异常值特性,拓展了全局灵敏度分析方法的适用范围。需要指出的是,本文假设模型为单个输出并且输入因子相互独立,当模型有多个输出或输入因子具有相关关系时,稳健的全局灵敏度分析方法将是一个值得关注的方向。2.2 基于稳健统计量的RDLR蒙特卡洛仿真计算方法

2.3 RDLR方法的实现步骤

3 算例分析
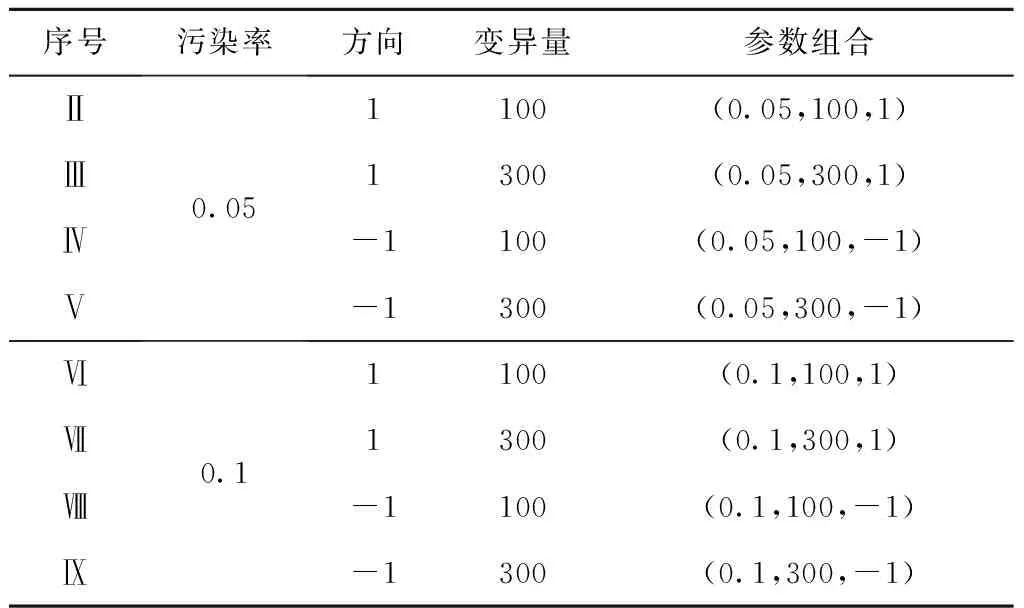
3.1 Ishigami函数




3.2 非线性偏态分布输出函数



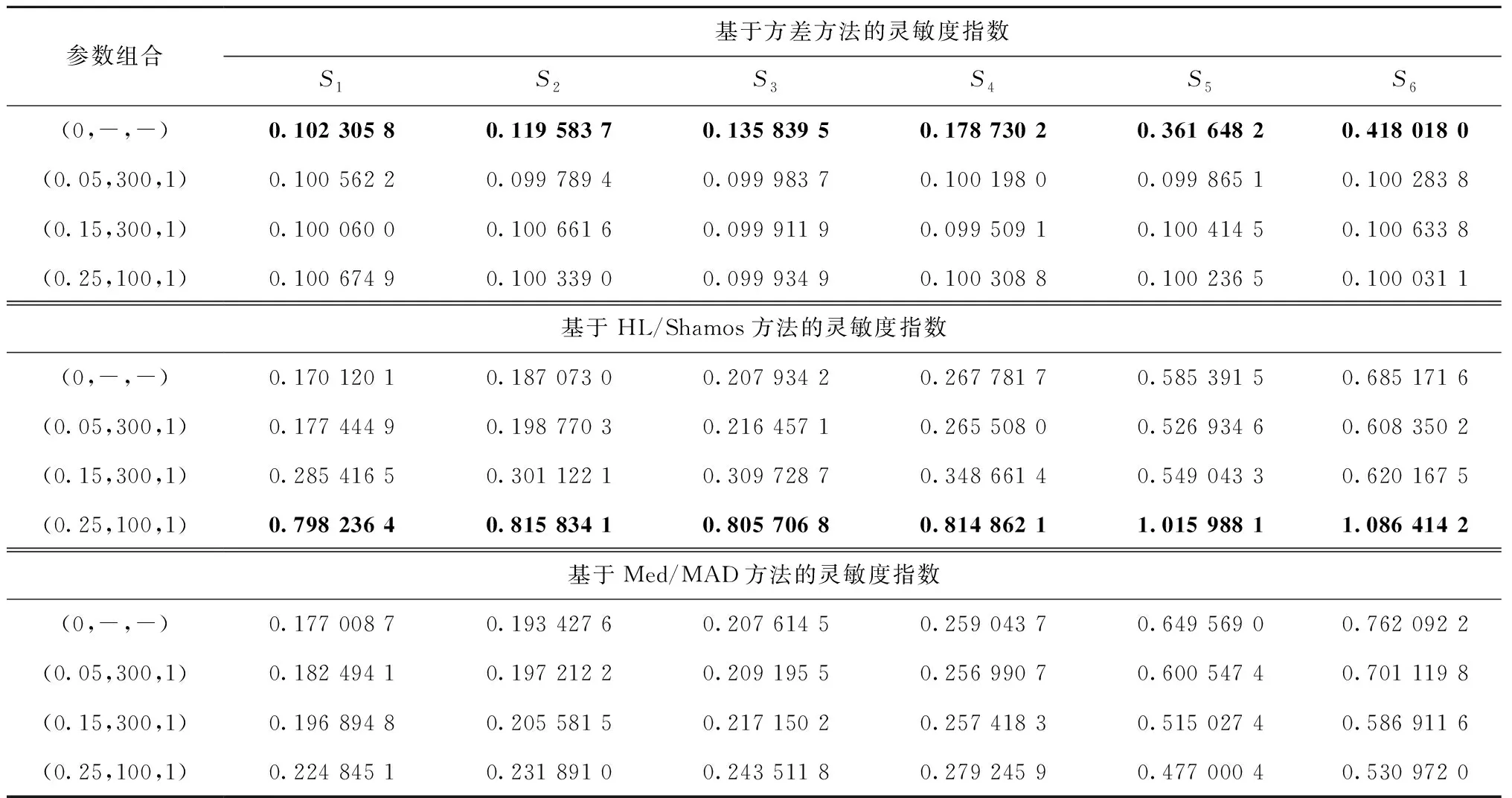
3.3 Sobol G-函数

4 结束语

