单支杆腹撑支架干扰测力及PIV试验研究

任凡凡，魏立辉，陶爱华，李雁鹏，杨磊，高娜，张彩成，蒋甲利，许相辉，王文达

航空工业空气动力研究院，哈尔滨 150000

0 引 言

国内外风洞试验工程师对支架干扰问题的研究主要集中在两方面：一是在满足风洞试验支撑系统刚度、强度要求的前提下，尽量减小支架干扰量，以降低支架干扰修正中大量相减带来的误差，提高风洞试验数据的准度；二是优化支杆的气动外形，提高支杆干扰的稳定性，实现支架干扰的准确测量与修正，保证和提高试验数据的精度[1-4]。

对于单支杆腹撑的支架干扰特性，郑新军等[1]在FL–9风洞中开展了不同截面支杆（圆截面支杆与24棱截面支杆、锥度支杆与等直段支杆）、不同模型机身与支杆直径比等一系列对比试验。针对低速风洞试验支架干扰问题也开展了一些其他工程应用研究，如王勋年等[5]对大迎角尾撑进行了研究，发现直支杆和预弯尾支杆的支架干扰量在中小迎角范围内随迎角变化不大，在大迎角状态下差异较大。沈彦杰等[6]对大幅振荡进行了研究，证明两步法可以去除支架的主要影响量。祝明红等[7]对大迎角张线尾撑进行研究发现，张线尾撑装置的横梁对飞机纵向的远场干扰量较小，大迎角区域内尾支杆对飞机纵向的近场干扰量较大。高静等[8]对推力矢量试验背撑的研究得出了背支杆在中等迎角以后（迎角α＞25°）对模型的升力、阻力会产生较大的负干扰并引起俯仰力矩改变的结论。田学诗[9]在20 世纪90年代采用测力和油流显示等试验方法，获得了一种采用24棱截面的固定转捩支杆，在雷诺数为0.2×106～0.5×106时，其气动特性及表面流动状态比圆截面支杆更稳定。该24棱支杆在FL-8风洞中被验证有效后，在中国航空工业空气动力研究院（简称气动院）的风洞中全面替换了圆截面支杆，系统地提升了气动院的支架干扰试验精准度。以上研究大多从测力试验展开[10-11]，公开资料中很少有人从支杆绕流与尾流特性方面进行分析。

针对FL-51风洞单支杆支架干扰问题，本文以减小腹撑支架干扰为目标，在FL-51风洞开展单支杆在不同截面形状、不同预置角等条件下的测力试验研究工作；并在FL-53风洞中开展PIV试验，以进一步分析不同尺寸、截面形状的二维支杆绕流与尾流特性。通过以上研究工作，获得不同截面形状、不同预置角支架的干扰量及其对比，同时获得各截面形状支杆的尾涡区宽度及支杆尾流的干扰区域。本研究可为提高FL-51风洞单支杆试验数据精准度提供技术参考。

1 风洞及支撑机构

FL-51风洞是一座开/闭口两用单回路连续式风洞，试验段截面为矩形，闭口试验段截面尺寸为4.5 m × 3.5 m × 11 m（宽 × 高 × 长），闭口空风洞最大风速为100 m/s。FL-51风洞内式应变天平单支杆腹撑系统主要包括回转转盘、迎角机构、单支杆、内式应变天平等。

FL-53风洞也是一座开/闭口两用单回路连续式风洞，试验段截面为矩形，闭口试验段截面尺寸为0.5 m × 0.375 m（宽 × 高），闭口空风洞最大风速为100 m/s，开口空风洞最大风速为85 m/s。本研究采用底部支撑方式，模型底部与转盘相连。模型姿态由偏航角机构和姿态角控制系统配合完成。采用的SPIV系统由TSI公司研制，激光器为镭宝公司生产的集成式双Nd:YAG激光器，互/自相关CCD摄像机为PowerView™ Plus 4MP 630059。采用便携式压力雾化示踪粒子发生器产生所需的粒子，粒子介质为橄榄油，产生的示踪粒子直径约为1～2 µm。

2 单支杆腹撑支架干扰测力试验

2.1 试验方法

采用FL-51风洞单支杆支撑系统进行试验，试验风速分别为70和50 m/s。假支杆连接在天平的固定端，不与模型接触，可与模型同时运动以保证试验在不同迎角下顺利进行。

采用两步法进行支架干扰测量，模型反装，以背撑为辅助支撑，以与不带腹撑假支杆背撑测力结果的差值为支架干扰量Fz。不带腹撑假支杆测得的气动力值为Fm，带腹撑假支杆测得的气动力值F=Fm+Fz。试验纵向结果以气流坐标轴系给出，横向结果以机体体坐标轴系给出。

2.2 试验内容

基于某飞机模型进行24棱支杆、圆截面支杆和截断翼型截面支杆支架干扰的测量试验。其中，不同截面形状单支杆腹撑三维支杆的支架干扰特性风洞试验内容如表1所示，单支杆腹撑不同预置角支杆的支架干扰特性试验内容如表2所示。

表1 3种截面三维支杆支架干扰特性测量试验内容Table 1 Support interference characteristics measurement test contents of three-dimensional support rod with three kinds of cross section

表2 3种截面三维支杆不同预置角支架干扰特性测量试验内容Table 2 Support interference characteristics measurement test contents of three-dimensional support rod with three kinds of cross section and different pre-deflection angles

2.3 试验结果

因该模型巡航构型（0°后襟，下同）与30°后襟状态支架干扰对比规律相近，故本文研究以巡航构型为主。该模型迎角为8°时，24棱、圆截面和截断翼型截面支杆的横向支架干扰量变化趋势与迎角为0°时基本一致，故本文的分析以0°迎角为主。

2.3.1 不同截面形状支杆

图1和2为24棱、圆截面和截断翼型截面支杆的支架干扰量对比曲线，图中ΔCL为升力系数支架干扰量，ΔCD为阻力系数支架干扰量，Δ Cma为气流轴俯仰力矩系数支架干扰量，ΔCl为滚转力矩系数支架干扰量，ΔCnb为偏航力矩系数支架干扰量，ΔCC为侧力系数支架干扰量。从图中可以看出，24棱、圆截面支杆支架干扰基本一致。相对于24棱支杆，截断翼型截面支杆产生负向的升力系数支架干扰，阻力系数支架干扰线性较好，气流轴俯仰力矩系数干扰量降低一半。截断翼型截面支杆在阻力系数干扰量和气流轴俯仰力矩系数干扰量方面更有优势。圆截面支杆的横向支架干扰量优于24棱支杆，但24棱支杆横向支架干扰曲线的线性度优于圆截面支杆。纵向支架干扰较优的截断翼型截面支杆在横向恶化，支架干扰量相对较大。

图1 3种截面支杆的纵向支架干扰对比（风速 70 m/s，0°后襟）Fig.1 Comparison of longitudinal strut support interference with three kinds of cross section（wind speed is 70 m/s, flap is 0°）

图3和4为从巡航状态变化到30°后襟状态时的24棱支杆和截断翼型截面支杆的支架干扰量对比曲线，表3为大部分的变化范围。可以看出，截断翼型截面支杆的纵向支架干扰量变化明显小于24棱支杆，且阻力支架干扰量线性度明显优于24棱支杆，故在纵向试验中，截断翼型截面支杆在数据准度和重复性精度方面都优于24棱支杆。采用截断翼型截面支杆进行不同构型纵向试验时，共用巡航构型下的支架干扰即可满足要求。滚转力矩系数支架干扰量和偏航力矩系数支架干扰量变化都较大，因此以24棱和截断翼型截面支杆进行不同构型横向试验时，需采用对应构型的支架干扰。

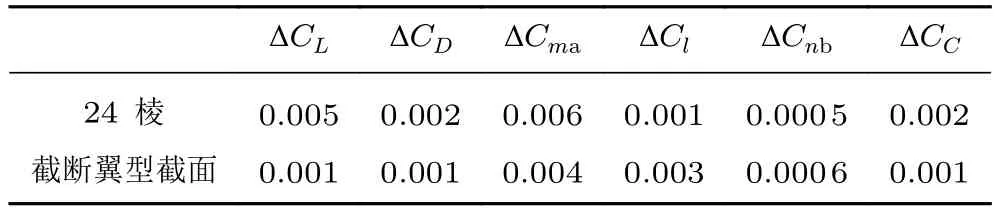
表3 24棱和截断翼型截面支杆不同构型支架干扰差量Table 3 Support interference difference of 24 ribbed and truncated airfoil support rods with different configurations

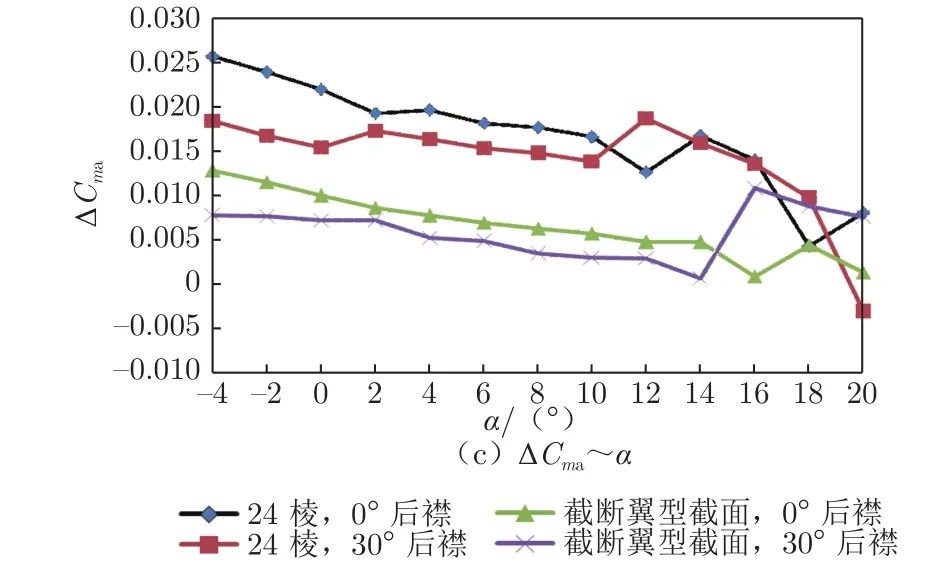
图3 后襟不同偏度的纵向支架干扰对比（风速 50 m/s）Fig.3 Comparison of longitudinal support interference with different bias at the back（wind speed is 50 m/s）

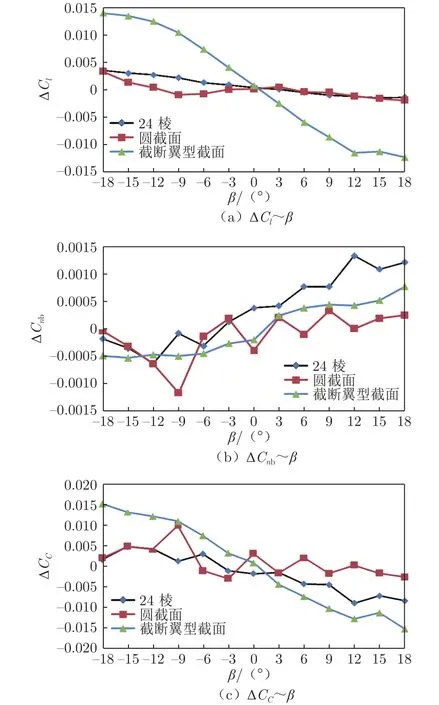
图2 3种截面支杆的横向支架干扰对比（风速 70 m/s，0°迎角，0°后襟）Fig.2 Comparison of transverse support interference with three kinds of cross section（wind speed 70 m/s, angle of attack is 0°, flap is 0°）

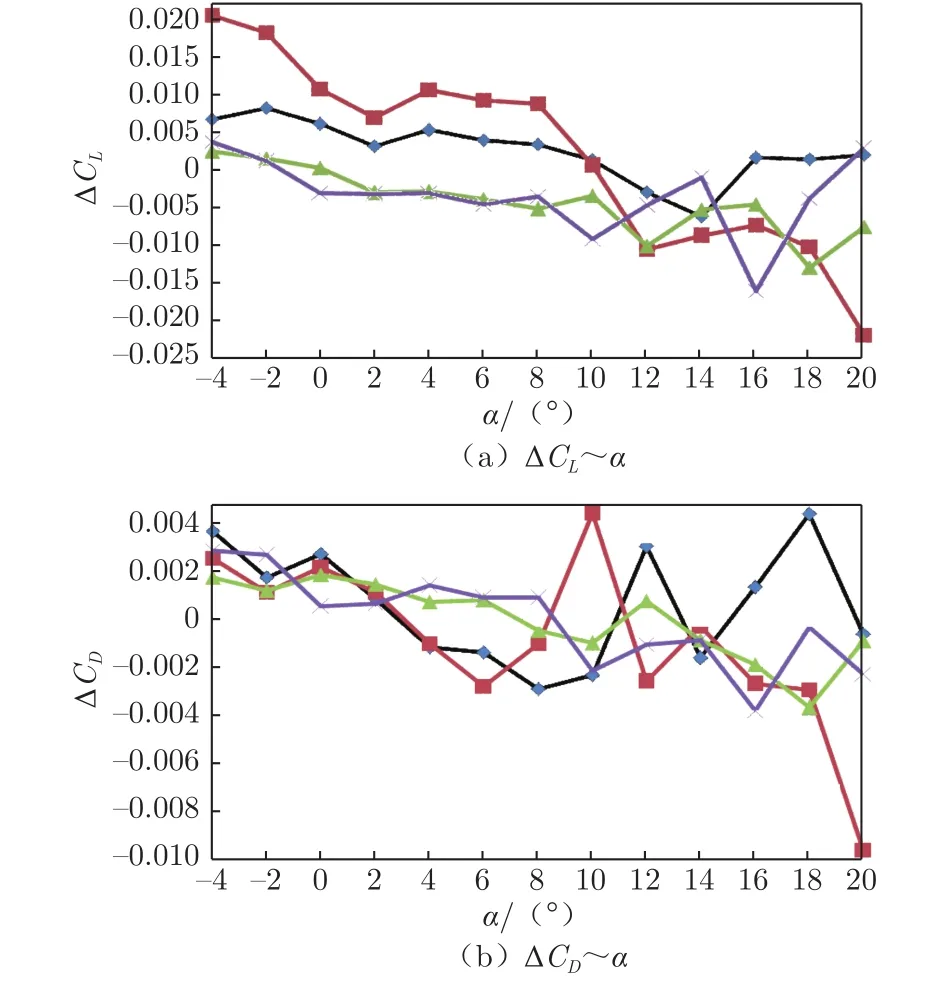
图4 后襟不同偏度的横向支架干扰对比（风速 50 m/s，0°迎角）Fig.4 Comparison of transverse support interference with different bias at the back（wind speed is 50 m/s, angle of attack is 0°）

图5～8给出了风速为70和50 m/s时的24棱支杆和截断翼型截面支杆的支架干扰量对比曲线，表4给出了大部分变化范围。从表中可以看出：巡航构型和30°后襟时，除阻力外，截断翼型截面支杆的纵向支架干扰量变化明显小于24棱支杆，且阻力支架干扰量线性度明显优于24棱支杆，故采用截断翼型截面支杆的纵向试验在数据准度和重复性精度方面都优于24棱支杆。采用截断翼型截面支杆进行巡航构型纵向试验时，不同风速时共用风速70 m/s下的支架干扰即可满足要求。滚转力矩系数支架干扰量和偏航力矩系数支架干扰量变化都较大，以24棱支杆和截断翼型截面支杆进行横向试验时，不同风速需采用对应风速的支架干扰。

表4 24棱和截断翼型截面支杆不同风速支架干扰差量Table 4 Support interference difference of 24 ribbed and truncated airfoil support rods with different wind speeds

图5 巡航状态不同风速的纵向支架干扰对比Fig.5 Comparison of longitudinal support interference with different wind speeds in cruise state

图6 巡航状态不同风速的横向支架干扰对比（0°迎角）Fig.6 Comparison of transverse support interference with different wind speeds in cruise state（angle of attack is 0°）

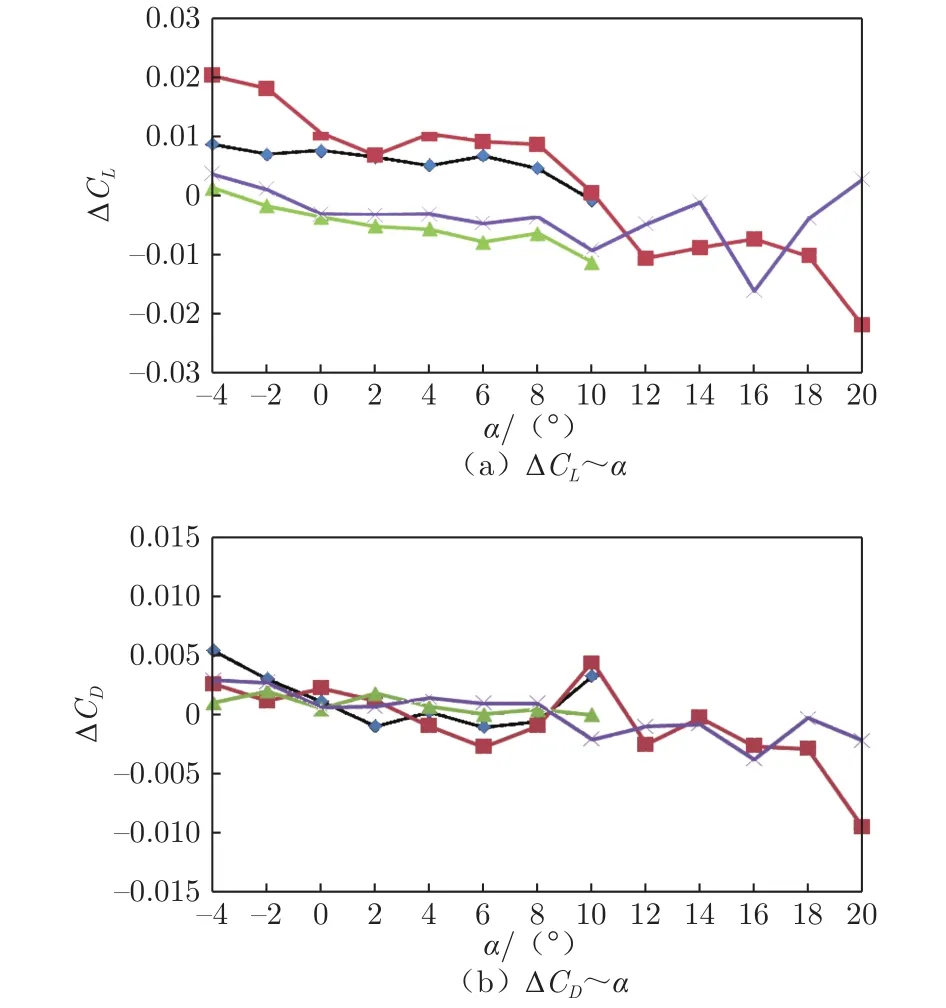
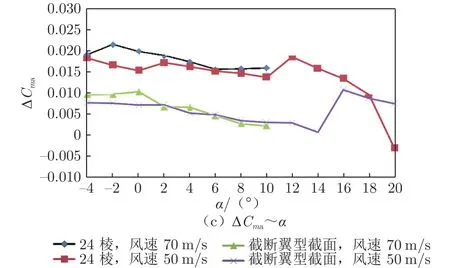
图7 30°后襟不同风速的纵向支架干扰对比Fig.7 Comparison of longitudinal support interference with different wind speeds and 30 degrees at the back

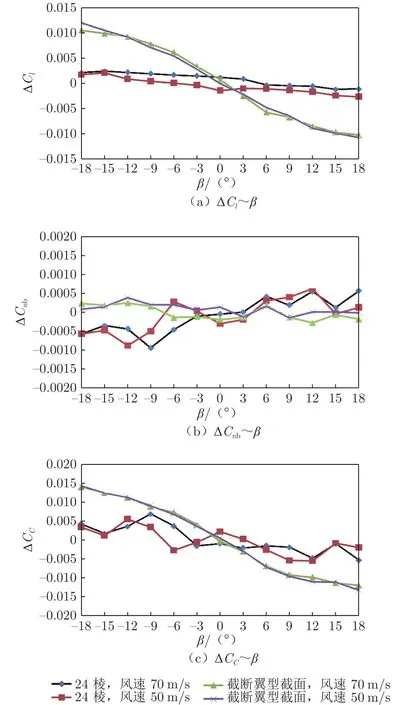
图8 30°后襟不同风速的横向支架干扰对比（0°迎角）Fig.8 Comparison of transverse support interference with different wind speeds and 30 degrees at the back（angle of attack is 0°）

2.3.2 不同预置角支杆

图9和10为支杆预置角从11°增大到60°时的24棱支杆、圆截面支杆和截断翼型截面支杆的支架干扰量对比曲线，表5给出了大部分变化范围。从表中可以看出：24棱支杆和圆截面支杆的纵向支架干扰差量较大，分别用二者进行纵向试验时，增大支杆预置角有利于提高纵向试验的准度和精度；截断翼型截面支杆的纵向支架干扰差量较小，以其进行纵向试验时，增大支杆预置角对纵向试验准度和精度的影响可以忽略不计。采用24棱支杆和圆截面支杆进行横向试验时，增大支杆预置角对横向试验的准度和精度影响不大；采用截断翼型截面支杆进行横向试验时，增大支杆预置角有利于提高横向试验的准度和精度。

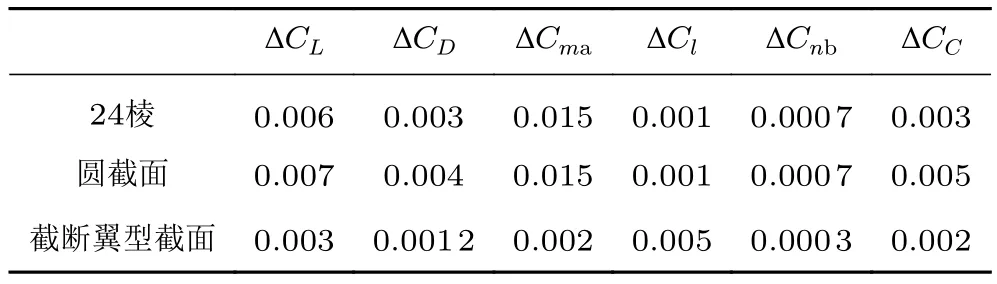
表5 24棱支杆、圆截面支杆和截断翼型截面支杆预置角11°和60°的支架干扰差量Table 5 Support interference differences of 24 ribbed support rods，round support rods and truncated airfoil support rods with pre-deflection angles of 11° and 60°

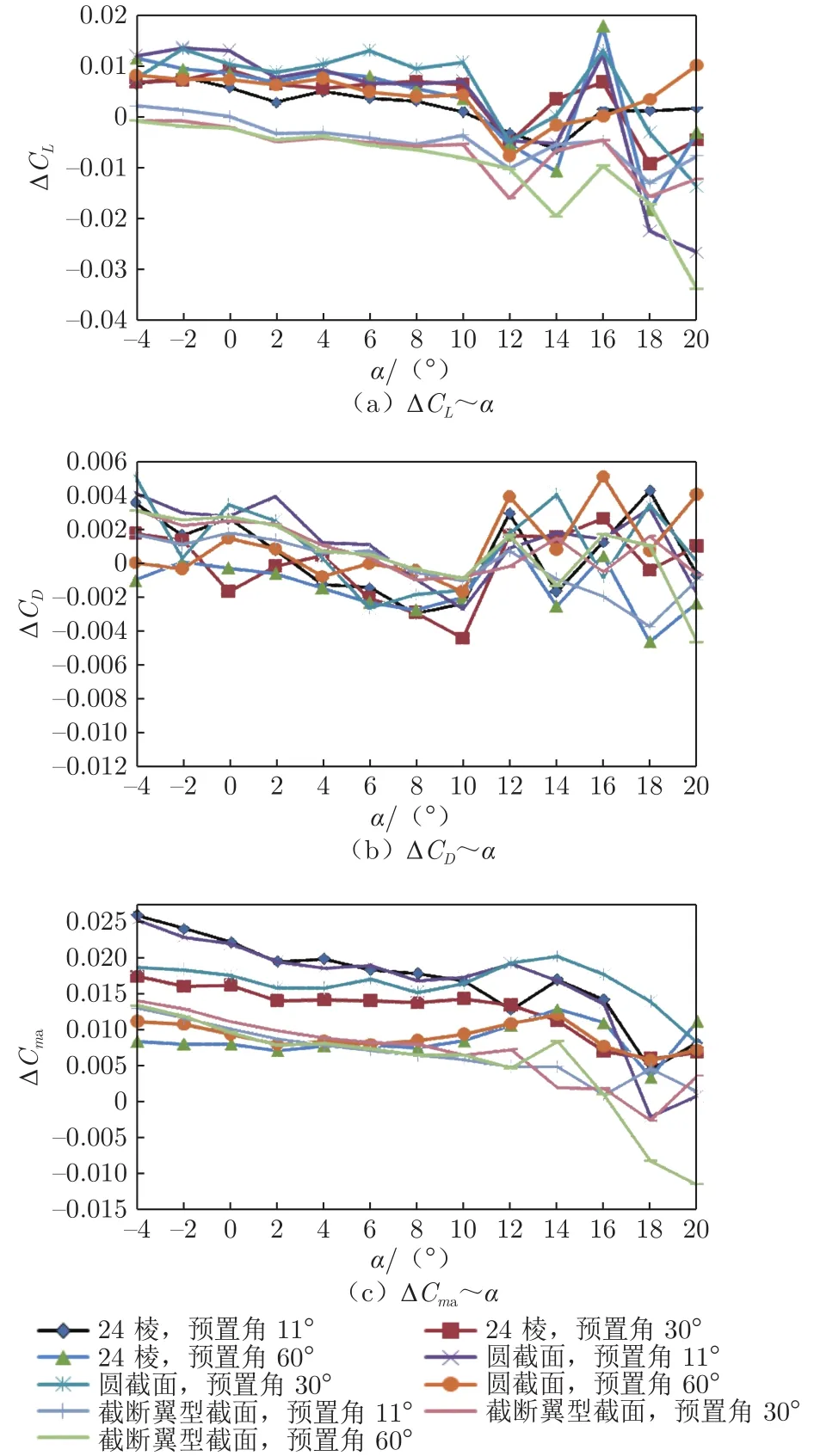
图9 不同预置角的纵向支架干扰对比（风速 50 m/s，0°后襟）Fig.9 Comparison of longitudinal support interference with different pre-deflection angles（wind speed is 50 m/s, flap is 0°）

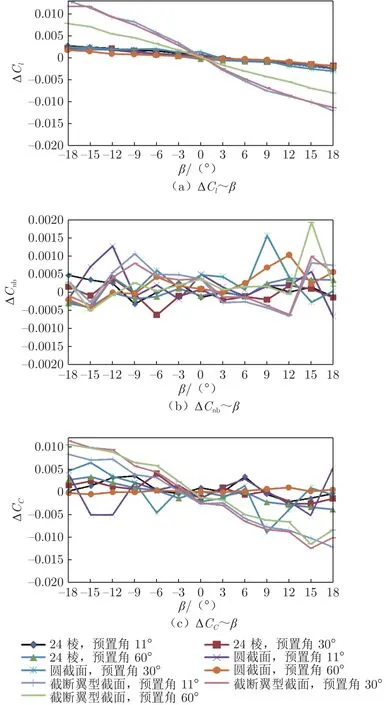
图10 不同预置角的横向支架干扰对比（风速 50 m/s，8°迎角，0°后襟）Fig.10 Comparison of transverse support interference with different pre-deflection angles（wind speed is 50 m/s, angle of attack is 8°, flap is 0°）

3.1 试验模型与状态

图11为二维支杆模型在风洞中的安装示意图，图12为各种二维支杆截面形状示意图，因其直径或最大厚度为50和120 mm时与80 mm时的截面形状相似，且FL-51风洞单支杆直径为80 mm，故图12仅给出了80 mm的示意图；表6为具体试验内容。

表6 二维支杆绕流与尾流特性PIV试验内容Table 6 PIV test content of two-dimensional support rod flow around and wake characteristics

图11 二维支杆绕流与尾流特性试验示意图Fig.11 Schematic diagram of two-dimensional support rod flow around and wake characteristics test

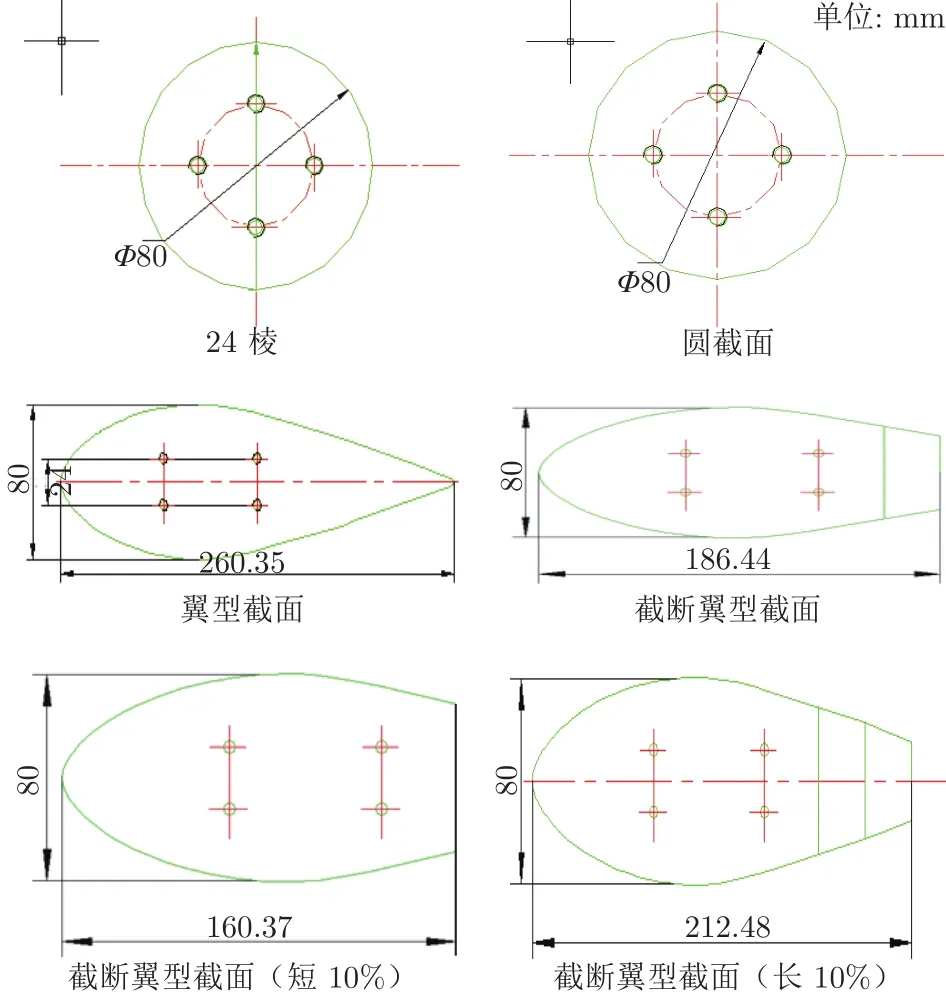
图12 各种二维支杆截面形状示意图Fig.12 Schematic diagram of two-dimensional support rods with various cross section shapes

3.2 试验结果分析

图13为直径（或最大厚度）为80 mm的各截面形状支杆（限于篇幅，略去了直径或最大厚度为50 mm的结果）在风速70 m/s、0°迎角（带模型试验时的侧滑角）时的支杆尾涡分布对比图，图中x为尾涡的流向，y为尾涡的宽度方向。表7为直径（或最大厚度）为50和80 mm的各截面支杆尾涡区前段的宽度情况。

表7 各截面支杆尾涡区前段的宽度Table 7 The trailing vortex region's front section width of support rodwith various cross section

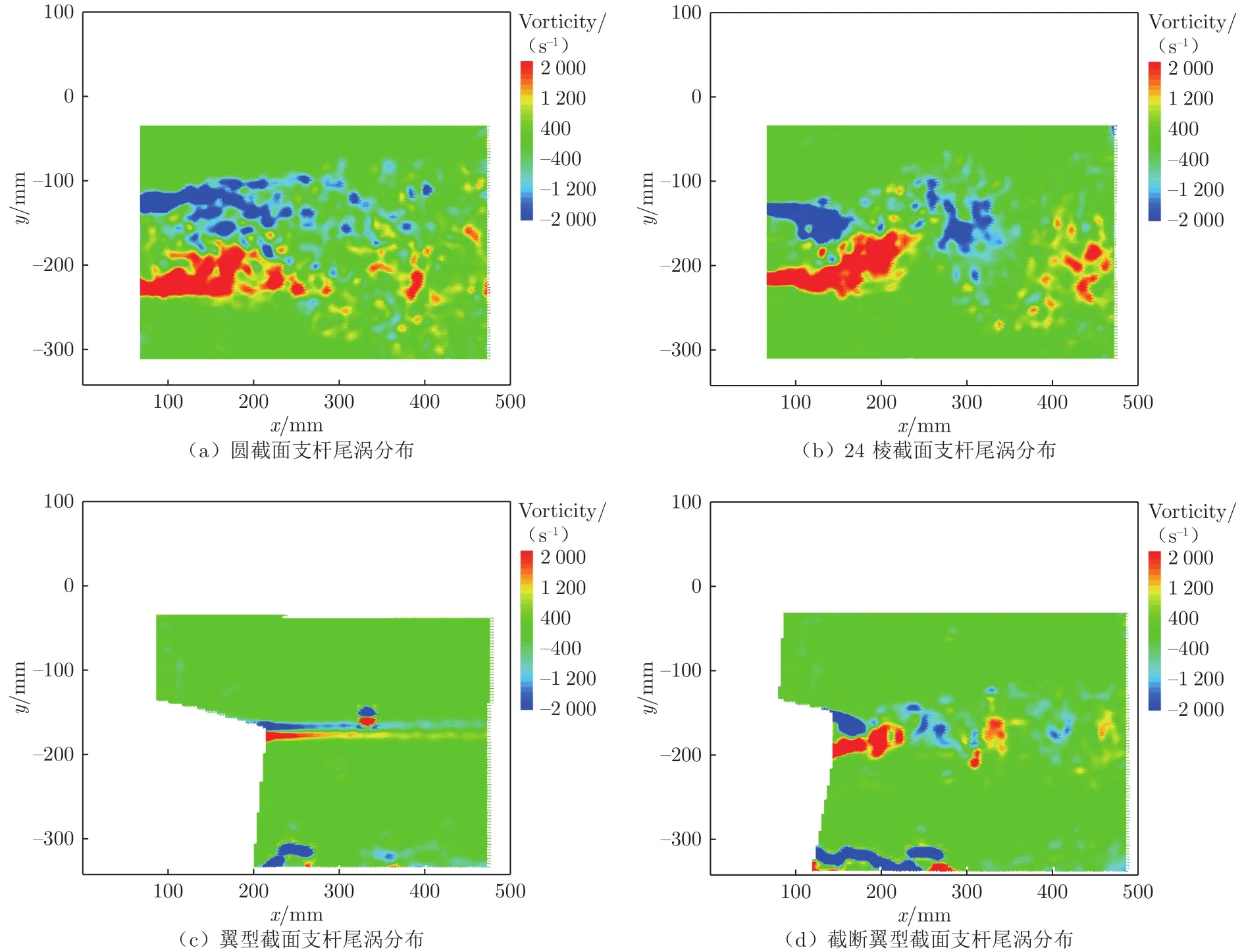
图13 直径/最大厚度80 mm各截面形状支杆尾涡分布图Fig.13 The trailing vortex distribution diagram of support rods with various cross section shapes and diameter/maximum thickness of 80 mm

从图中和表中可以看出，在相同风速下，相同直径（或最大厚度）支杆的尾涡区宽度由小到大依次为：翼型支杆，截断翼型长10%支杆，截断翼型支杆，截断翼型短10%支杆，24棱支杆和圆截面支杆。可见，对于带模型状态下的纵向试验，支杆宜选择翼型截面或者适当截断的翼型截面。

圆截面支杆和24棱支杆直径由50 mm增大到80 mm时，其尾涡宽度也相应增大了30 mm左右；翼型截面和各截断翼型截面支杆最大厚度增大，而尾涡区宽度基本不变。可见，随着最大厚度的增大，翼型截面和各截断翼型截面支杆的尾涡具有较好的一致性；而24棱支杆和圆截面支杆的尾涡则随直径增大存在一定的变化。由此可知，风洞试验选择翼型截面支杆时可适当加大支杆的尺度（而尾涡区的宽度基本不变），这更有利于提高支杆刚度，以及满足某些特殊试验通高压气或安装大量传感器线缆的需求。

与24棱支杆相比，截断翼型截面支杆的尾涡宽度小且具有较好的一致性，从流动现象层面解释了前文支架干扰测力试验得出的结论，即纵向试验采用截断翼型截面支杆优于24棱支杆。

图14为直径80 mm的24棱支杆在风速70 m/s、迎角分别为0°和7.5°时的尾流涡量图。从图中可以看出，当二维24棱支杆的迎角（带模型试验时的侧滑角）变化时，其尾流区宽度变化很小且具有较好的一致性。

图14 24棱支杆变迎角下的尾流涡量图Fig.14 Wake vorticity diagram of 24 ribbed support rodsat varying attack angles

图15和16为最大厚度为50 mm的翼型截面支杆和截断翼型长10%支杆（限于篇幅，略去了截断翼型截面支杆、截断翼型截面长10%支杆）在风速70 m/s以及迎角-8°、-16°和-30°（带模型试验时的侧滑角）时的尾流涡量图。从图15和16可以看出，迎角从-8°变化到-16°，支杆的尾涡区都有变宽的趋势，其中仅翼型截面支杆尚能保持较小的尾涡区宽度，翼型截面支杆在迎角-16°时尾涡区宽度就已超过了翼型的最大厚度。迎角达到-30°时，因流动分离，翼型截面支杆的尾涡区宽度显著增大，基本略大于支杆在垂直气流方向的尺度。

图15 翼型截面支杆变迎角下的尾流涡量图Fig.15 Wake vorticity diagram of airfoil support rods at varying attack angles

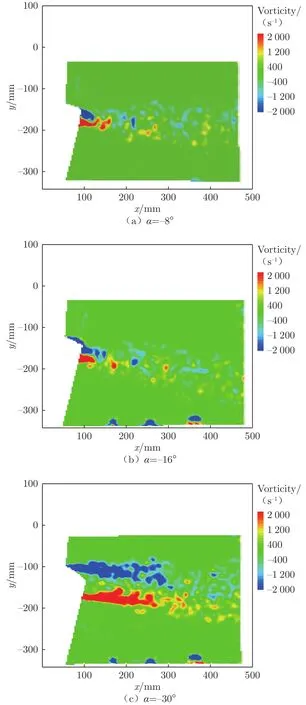
图16 截断翼型截面短10%支杆变迎角下的尾流涡量图Fig.16 Wake vorticity diagram of truncated airfoil and 10% shorter support rods at varying attack angles

与截断翼型截面支杆相比，24棱支杆的尾涡宽度随迎角（风洞试验时的侧滑角）的变化较小且具有较好的一致性，从流动现象层面解释了前文支架干扰测力试验得出的结论，即与24棱支杆相比，纵向支架干扰较优的截断翼型截面支杆的横向干扰恶化，支架干扰量相对较大。

4 结 论

圆截面支杆与24棱支杆支架干扰量类似，采用24棱支杆进行不同构型、不同风速纵横向试验时基本都需进行对应构型、风速下的支架干扰试验，增大支杆预置角有利于提高纵向试验的准度和精度；截断翼型截面支杆的阻力和俯仰力矩支架干扰量较小，纵向支架干扰较优的截断翼型截面支杆的横向干扰恶化，支架干扰量相对较大；采用截断翼型截面支杆进行不同构型、不同风速纵向试验时共用巡航构型、风速70 m/s下的支架干扰即可满足要求，横向试验时则需采用对应构型、风速下的支架干扰，增大支杆预置角有利于提高横向试验的准度和精度。

随着最大厚度的增大，翼型支杆和各截断翼型截面支杆的尾涡具有较好的一致性；而24棱支杆和圆截面支杆的尾涡则随着直径变化存在一定的变化。对于仅进行纵向试验或以纵向试验为重点的风洞试验，支杆宜选择翼型截面或者适当截断的翼型截面；此外，选择翼型截面支杆还可适当加大支杆的尺度（其尺度加大而尾涡区的宽度基本不变），有利于提高支杆刚度以及满足某些特殊试验通高压气或安装大量传感器线缆的需求。与24棱支杆相比，迎角（风洞试验时的侧滑角）为0°时截断翼型截面支杆的尾涡宽度小且具有较好的一致性，但随迎角变化较大且一致性不好，从流动现象层面解释了支架干扰测力试验得出的结论，即纵向试验采用截断翼型截面支杆优于24棱支杆；与24棱支杆相比，纵向支架干扰较优的截断翼型截面支杆的横向干扰恶化，支架干扰量相对较大。