基于激光雷达回波的动态尾涡特征参数计算

赵丽雅，谷润平，魏志强

(中国民航大学空中交通管理学院，天津，300300)

飞行安全间隔很大程度上受限于飞机翼尖产生的尾涡，对尾涡特征参数的分析有助于提高机场跑道利用率、减少飞机延误，而通过激光雷达探测特定区域内的尾涡并解算其特征参数是一种重要的研究手段。

Rahm等[1]利用机载多普勒雷达测量大型飞机在自由大气中的尾涡，通过对探测数据的处理得到尾涡运动轨迹。徐世龙等[2]从飞机尾涡激光探测的总体要求出发，设计了尾涡相干激光探测系统的结构与参数。牛凤梁等[3]对降雨条件下飞机尾流的雷达特性进行研究，得到尾流中雨滴数密度分布特性，基于某雷达参数通过信号处理得到降雨条件下飞机尾流的雷达回波，并发现了其独特的多普勒特性。Wu等[4]在北京首都国际机场利用激光雷达探测飞机尾涡，对雷达探测系统及探测方式进行了详细讨论。Penkin等[5]在俄罗斯机场利用多普勒激光雷达探测到B737-800飞机的尾涡并进行了动力学分析。Hon等[6]介绍了香港国际机场的飞机尾涡观测计划及初步数据分析结果。上述研究主要利用雷达探测尾涡轨迹，并定性分析了尾涡的位置与强度变化，没有对尾涡的特征参数进行定量反演计算。

利用雷达回波对尾涡特征参数进行定量研究的成果也有不少。Köpp等[7]在Tarbes机场对大型飞机产生的尾涡进行探测，并利用速度包络法设计了距离-高度显示器(range-height indicator，RHI)扫描方式下的尾涡特征参数反演算法。吴永华等[8]研究了飞机尾涡激光探测技术，给出激光探测方式和探测系统的参量。徐世龙等[9]利用速度包络法设计了平面-位置显示器(plan-position indicator，PPI)扫描方式下的尾涡特征参数反演算法，并以某型号飞机的激光雷达探测实验数据为例进行了计算。屈龙海[10]围绕飞机尾流雷达探测需求，研究了晴空、云雾以及降雨条件下飞机尾流的雷达散射特性。Smalikho等[11-12]利用“Stream-Line”脉冲相干多普勒激光雷达对飞机尾涡进行探测，提出了根据雷达数据估计尾涡轨迹的方法，并采用径向速度法估算飞机尾涡的特征参数。Loaec等[13]用激光雷达探测不同机型的尾涡强度，分析了背景风场的影响。Darracq等[14]鉴于机载雷达的位置特殊性，设计了利用轴向速度推演尾涡特征参数的算法。

上述研究中提出的算法多是针对静态尾涡的特征参数反演，没有考虑在实际大气中尾涡的强度消散和涡核下沉，影响到特征参数的计算精度。本文从飞机尾涡的物理模型出发，分析尾涡附近的径向速度场与特征参数的关系，并结合尾涡的运动及消散模型，建立动态尾涡特征参数反演算法。最后通过仿真实验来验证该算法的有效性。

1 飞机尾涡的物理模型

1.1 尾涡环量模型

飞机尾涡的强度一般用涡旋环量Γ来表示。在理想无黏气体中，流场内的环量处处相等且保持不变。但通常情况下，在涡旋中心处受到空气黏性影响较大，其环量为零，而且涡旋环量随着时间的变化也会逐渐减小。同时，由于相互之间的诱导作用和重力因素，涡旋形成之后会一边旋转扩散一边下降。

在尾涡刚刚形成还没有扩散衰减时，初始环量Γ0取决于飞机的质量、速度、翼展等参量[15]：

(1)

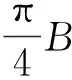
1.2 尾涡速度模型

尾涡旋转速度直接关系着尾涡的形状、大小和演化进程。尾涡速度模型很多，本文选用Hallock-Burnham模型描述尾涡切向速度分布。该模型与尾流的拟合度好、形式简单、速度变化相对比较平滑。与涡核中心距离为r的某一点的切向速度VT为：

(2)

式中:rc为涡核半径。涡核半径为各个方向上切向速度最大值的点与涡核的距离，通常为(3%～5%)b0。

1.3 尾涡消散模型

尾涡消散分为两个阶段：扩散阶段和快速消散阶段。在扩散阶段，尾涡消散的速度非常慢，其强度近似认为不变；在快速消散阶段，尾涡强度迅速减小。设尾涡扩散阶段的持续时间为tc，同时为了计算方便，通常还定义相对于基准参数的无量纲参数——参考时间t0与参考下沉速度ω0：

(3)

在尾涡扩散阶段其强度消散约为10%，且与时间倒数近似为负指数关系，扩散阶段的尾涡消散模型为[16]：

(4)

经过时间tc后，尾涡消散会加快，快速消散阶段的尾涡消散模型为[16]：

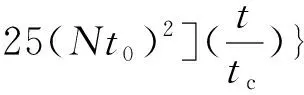
(5)

式中：N为浮力频率。

1.4 尾涡下沉模型

尾涡产生以后，不仅随着时间逐渐消散，并且由于相互的诱导作用而向下运动。尾涡下沉速度ω与涡核间距及涡核半径有关[17]：

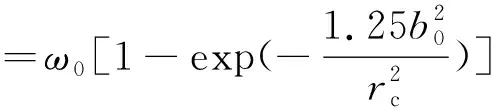
(6)

尾涡经过t秒后下降的高度h按下式计算：

ωdt

(7)

式中：h0为初始尾涡高度。

2 静态尾涡特征参数计算方法

2.1 径向速度

如图1所示，激光雷达对飞行中的飞机左右机翼产生的一对尾涡进行扇形扫描。分别以激光雷达中心和两个涡核的中点为坐标原点建立坐标系YOZ和Y′O′Z′，RO为两个坐标原点之间的距离。设涡核中心分别为O1和O2，其与激光雷达的径向距离为R1和R2。选取尾涡流场内任意一点P作为研究对象，P与激光雷达的距离为R，激光雷达扫描到P点时的探测角度为φP，αP为尾涡径向速度与Y轴的夹角。

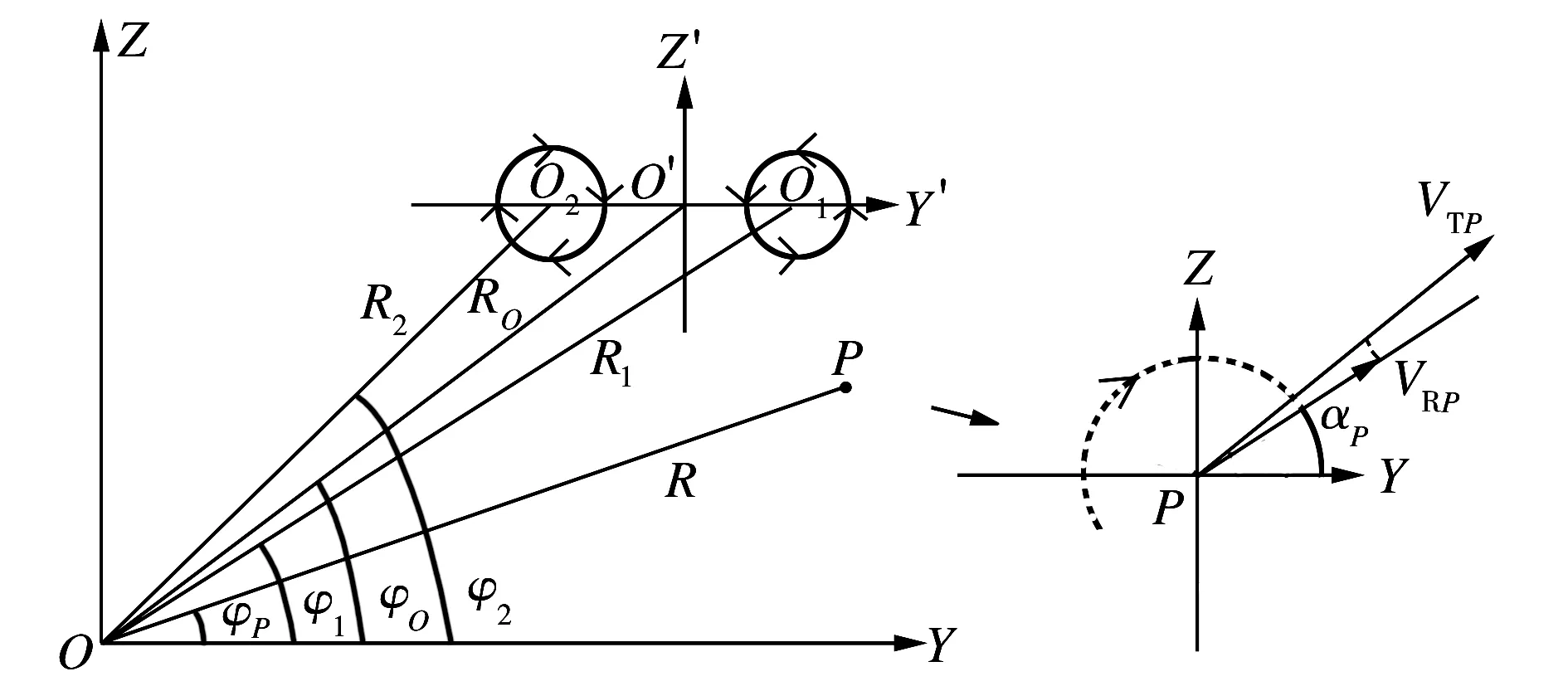
图1 径向速度计算示意图

Fig.1Schematicdiagramofthecalculationofradialvelocity

激光雷达测量尾涡流场的速度实质上是测量大气分子或气溶胶粒子的运动速度，所以只有与激光波束传播方向一致的速度分量才能引起后向散射光信号的多普勒频移。本文使用RHI扫描方式，扫描结果只能获取尾涡剖面上各点速度沿激光波束的径向分量，即切向速度在扫描径向上的投影值，称为径向速度VR。通过图1所示的坐标关系，利用式(2)计算出尾涡附近某一点P受到单个涡影响时的径向速度为：

αP-φP)

(8)

同时由式(8)可推导出尾涡流场内任意一点受到两个涡影响时的径向速度为[7]：

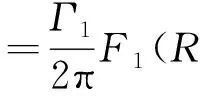
(9)

其中，

Fl(R,φ)=

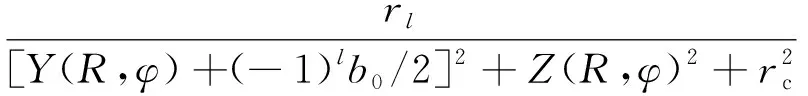
rl=ROsin(φ-φO)-(-1)l(b0/2)sinφ，

Y(R,φ)=Rcosφ-ROcosφO，

Z(R,φ)=Rsinφ-ROsinφO。

式中：l为尾涡编号，l=1代表右涡，l=2代表左涡。

通过分析可知rc与其他数值相比较小，可以忽略不计，为方便计算同时又不失精度，将上式中的Fl(R,φ)简化为：

(10)

2.2 涡核位置

让激光雷达在预定义区域内扫描，将探测到的回波数据进行降噪、插值等处理后，得到有较高速度分辨率的多普勒谱，利用各个探测单元内的多普勒谱计算出尾涡径向速度。在每个探测单元的多普勒谱中选取适当的门限值，如图2所示，该门限值与多普勒谱的交点即为尾涡流场中的速度正包络与负包络，分别记为Vmax与Vmin，代表各探测单元内径向速度的最大值和最小值。

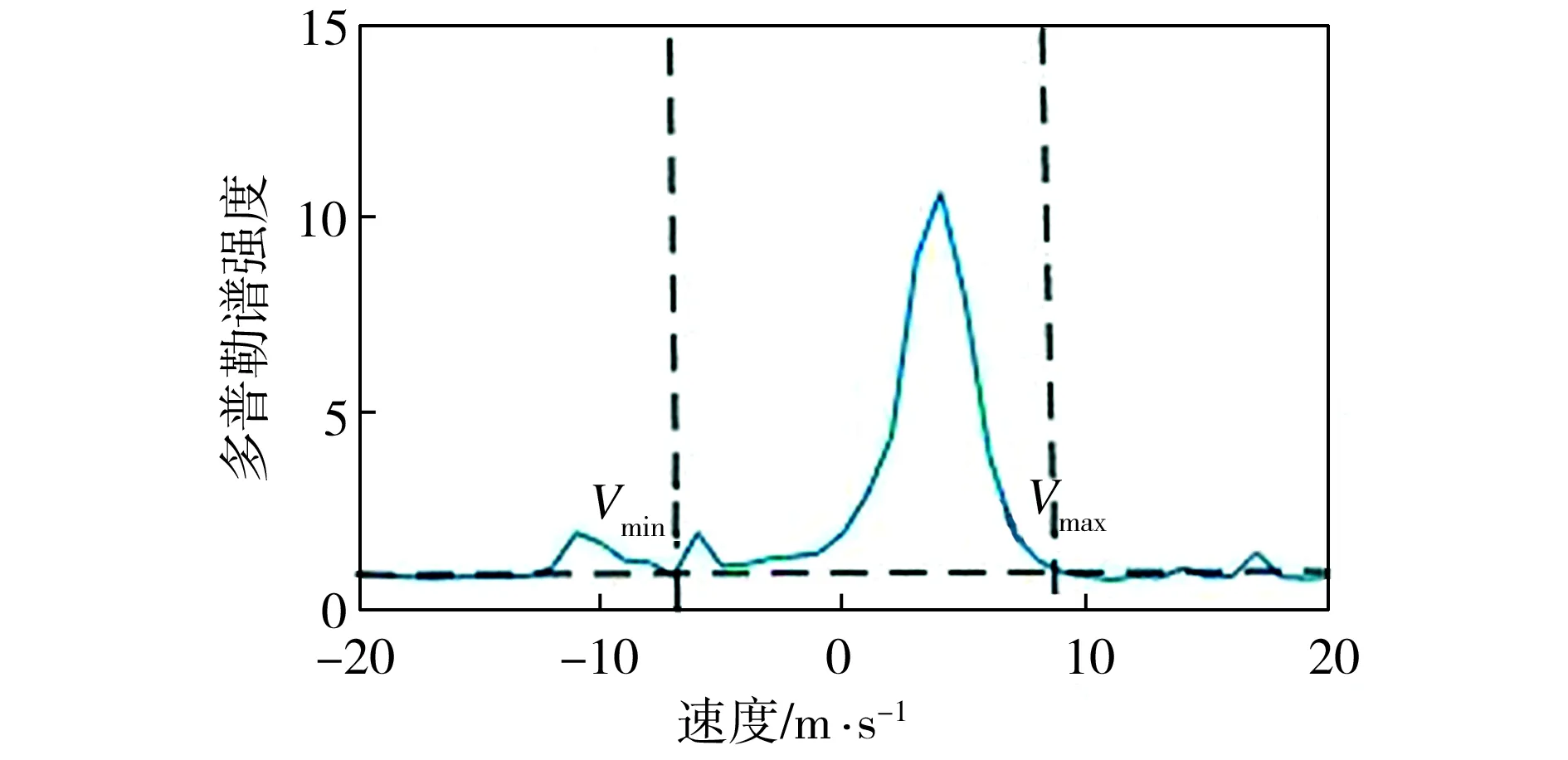
图2 利用多普勒谱得到的速度包络值

两个尾涡的位置可利用上述速度包络来确定。分别计算不同探测单元的正、负速度包络，如图3所示。选取正包络的最大值点A、B，其坐标

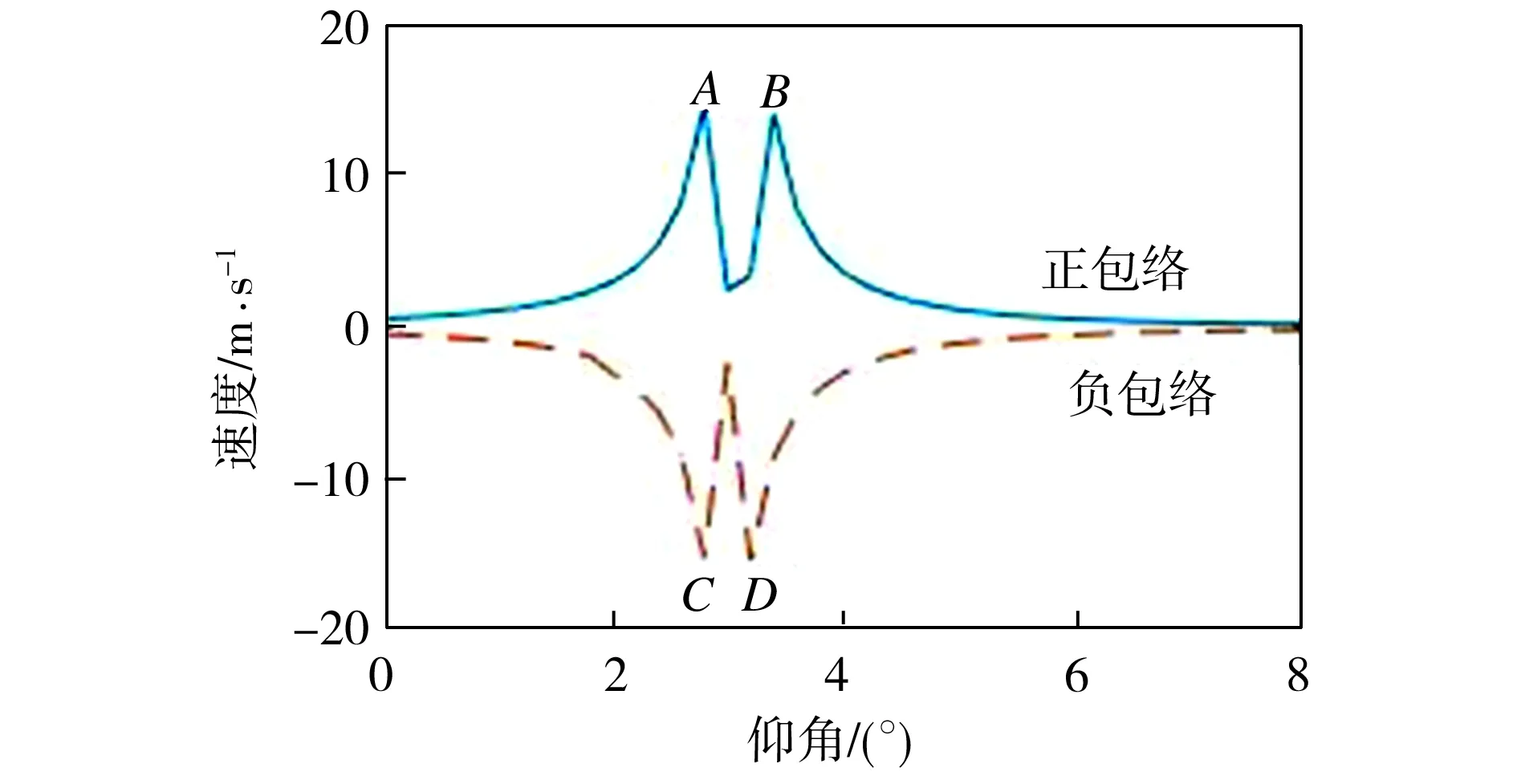
图3 正、负速度包络值

(11)

2.3 尾涡环量

速度包络值代表的是每个探测单元内径向速度的正向最大值和负向最小值，所对应的点为探测单元内的径向速度极值点，其导数为零，即

(12)

通过求解式(12)可得出：

(13)

计算出正、负包络上的速度理论值，将式(13)带入式(9)，得出：

(14)

式中：d(φ)=b0cosφ。式(14)所示即为每个单元内径向速度正向最大点或负向最小点的速度。

假设在尾涡流场中的某些位置只受到单个涡的影响，则可利用这些点的速度计算单个尾涡的环量大小。如图4所示，选取与激光雷达距离为R1、R2处的点i和k，探测到i、k点的激光雷达仰角分别为φi、φk。

图4 尾涡环量计算示意图

Fig.4Schematicdiagramofvortexcirculationcalculation

由式(14)推导出：

(15)

式中：Γ1ik与Γ2ik为利用i点和k点估算得到的两个尾涡的环量值。

选取与激光雷达的距离为R1的n个数据点以及与激光雷达的距离为R2的m个数据点进行计算，通过式(15)得到环量估计值Γ1ik和Γ2ik。将这些估算值求和后取平均值，得出根据径向速度计算尾涡环量的公式如下：

(16)

2.4 尾涡特征参数计算流程

综上所述，基于激光雷达回波的静态尾涡特征参数计算流程为：①激光雷达发射激光波束对尾涡周围进行扫描，并接受后向散射信号；②将接收到的信号进行降噪、傅里叶变换等信号处理得到多普勒谱；③选取门限值确定正、负速度包络，进而得到探测区域的径向速度分布；④利用径向速度分布，通过式(11)反演得到涡核位置；⑤将涡核坐标值带入式(16)计算尾涡环量。

2.5 实例分析

2.5.1 静态尾涡流场

下面利用A320飞机的尾涡流场进行计算分析，飞机的相关参数如表1所示。

表1 A320飞机相关参数

假定尾涡形成后强度及高度不变，仿真出静态尾涡的激光雷达回波。激光雷达与机场跑道中轴线水平距离为700 m，探测开始时飞机距离地面约60 m，激光雷达扫描参数如表2所示。

表2 激光雷达扫描参数

经过对回波信号的处理和径向速度的解算，得到如图5所示的扫描区域径向速度分布。

图5 扫描区域径向速度分布

根据径向速度反演出不消散、不下沉的静态尾涡左右两涡的环量分别为283.9731、282.9731 m2/s，与表1中尾涡初始环量290m2/s比较接近。

2.5.2 动态尾涡流场

上述算法在计算静态尾涡环量时的精度较高，然而大气中尾涡产生后会不断下沉且逐渐消散，因此以下分析该算法在计算动态尾涡特征参数时的性能。

利用静态尾涡特征参数计算方法，结合尾涡下沉运动模型反演出两个尾涡的涡核高度，如图6中虚线所示，图中实线为利用式(7)计算得到的涡核高度随时间的变化情况，显然二者存在较大偏差，估算出的涡核位置较高。

图6 静态尾涡特征参数算法计算出的动态尾涡高度

Fig.6Heightofdynamicwakevortexcalculatedbythestaticvortexcharacteristicparameteralgorithm

尾涡下沉和消散都可能导致上述算法对环量估算精度的降低。本文根据尾涡下沉与消散的变化情况，仿真动态尾涡的回波信号，并利用该回波信号计算尾涡的特征参数，与尾涡流场内利用机型参数的计算结果进行对比。由于涡核附近流场速度会发生突变，可导致计算值存在一定偏差，因此利用探测到左涡涡核位置之前10 s的数据点以及探测到右涡涡核位置之后10 s的数据点进行计算，不同时刻下尾涡环量的计算结果如图7所示，其中实线为根据文献[15]中的研究结果得出的A320飞机尾涡环量消散情况。由图7可见，估算结果与尾涡流场的环量变化拟合度较差。

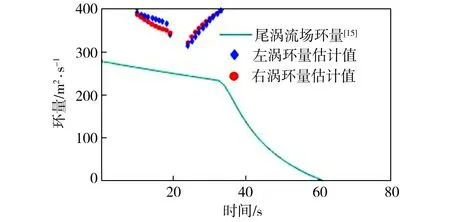
图7 静态尾涡特征参数算法计算出的动态尾涡环量

Fig.7Circulationofdynamicwakevortexcalculatedbythestaticvortexcharacteristicparameteralgorithm

将根据不同时刻的激光雷达探测数据计算得到的环量值加和取平均得到左、右尾涡环量的最终计算结果分别为365.63、363.67 m2/s，这与利用机型参数计算得到的环量值(290 m2/s)的误差在25%左右。

综上所述，对于静态尾涡，即在不考虑尾涡的消散和运动的情况下，式(11)～式(16)所代表的算法能够较为准确地计算出尾涡的特征参数。但实际中尾涡的位置与强度不断变化，通过该方法估算出的尾涡特征参数与尾涡流场内的实际情况相差较多，因此需要考虑尾涡的消散与下沉特性对算法进行优化，以提高特征参数计算精度。

3 尾涡特征参数计算方法的改进

3.1 涡核位置的计算

由于尾涡的下沉运动，其涡核位置会发生变化，故以下对式(11)中的静态尾涡涡核位置确定方法进行改进。

首先，通过式(11)找到涡核位置，即为当前探测时刻的涡核位置，解算出该时刻涡核与激光雷达之间的水平距离x及垂直距离y：

x=Rlcosφl,y=Rlsinφl

(17)

然后，根据尾涡的下降速度计算尾涡不同探测时刻t的涡核高度yt：

yt=y+ωt

(18)

最后，根据垂直距离重新计算每一个探测时刻t的尾涡距离Rlt和探测角度φlt：

(19)

3.2 尾涡环量的计算

根据式(19)计算出的涡核位置更接近大气中运动尾涡的实际位置，利用该结果反演出的尾涡环量也会更加精确。将式(19)替换式(16)中的Rl和φl(l=1,2)，得到只考虑尾涡下沉而不考虑消散的动态尾涡环量计算公式为：

(20)

然而，尾涡在下沉运动的同时，其环量也要逐渐衰减。公式(15)中，用于计算速度的环量应为不同时刻的环量值，即

(21)

式中：Γ10和Γ20为两个尾涡的初始环量;p(t)为尾涡消散函数;ti和tk分别为探测到i点和k点的时刻。

由式(21)推导出同时考虑尾涡下沉和尾涡消散的动态尾涡环量计算公式：

(22)

3.3 动态尾涡特征参数计算仿真

下面利用仿真的动态消散、下沉的尾涡流场作为参照组，与通过激光雷达回波计算得出的特征参数进行对比，分析改进算法的准确性。

首先，只考虑尾涡下沉的影响，利用式(20)估算出尾涡的环量大小，结果如图8中菱形和圆形线所示，图中实线为根据文献[15]得出的结果，虚线为根据尾涡消散模型(式(4)～式(5))得出的结果。由图8可见，估算出的尾涡环量偏小，这是因为公式(20)没有考虑尾涡的消散情况。但是与图7对比可以看出，即使只改进尾涡的涡核位置确定方法，最后的尾涡环量估算精度也有明显提高。

图8 只考虑尾涡下沉影响的优化算法计算结果

Fig.8Calculationresultsofoptimizationalgorithmonlyconsideringtheeffectofvortexdescent

然后，同时考虑尾涡消散和下沉的影响，通过式(22)估算出尾涡的初始环量。利用不同时刻的估算值，结合式(4)～式(5)的尾涡消散模型计算出不同时刻的尾涡环量值，其结果如图9所示。从图9来看，利用式(22)估算出的尾涡初始环量更接近尾涡消散模型和文献[15]的研究结果。

将上述实验结果中不同时刻估算的初始环量值求和取平均得到最终反演出的尾涡初始环量值。只考虑尾涡下沉影响因素时计算出的左、右尾涡初始环量分别为267.64、260.21 m2/s，对比通过机型参数计算出的尾涡初始环量290 m2/s，其误差分别约为7%与10%；而综合考虑尾涡消散和下沉因素时计算出的左、右尾涡初始环量分别为281.25、281.40 m2/s，其误差约为3%。前面2.5.2节的研究结果表明，不考虑尾涡下沉和消散影响的环量计算误差在25%左右。由此可以看出，与尾涡消散相比，尾涡下沉对尾涡环量的估算精度影响更大。这是因为，涡核位置影响到计算使用的数据点与涡核的距离r的大小，从而涉及每一个数据的计算，累计误差较大，导致环量计算偏差较大，而所选取用于计算的数据点处于涡核附近，这时尾涡还未进入或者刚刚进入快速消散阶段，环量衰减较小，故对最终的环量计算精度的影响程度相对较低。

图9同时考虑尾涡下沉和消散影响的优化算法计算结果

Fig.9Calculationresultsofoptimizationalgorithmconsideringtheeffectsofvortexdescentanddecay

4 结语

在实际情况中，飞机尾涡产生后是逐渐消散并且不断下沉的，而静态尾涡特征参数计算方法对尾涡环量的估算偏差较大。本文综合考虑了尾涡的消散和下沉因素，提出了利用激光雷达回波计算动态变化的飞机尾涡特征参数的方法。首先使用特定门限值提取尾涡流场的速度包络，解算出尾涡径向速度分布，然后利用该径向速度计算出涡核位置与尾涡环量。该方法能够更加准确地反演出动态尾涡环量。利用仿真的动态尾涡流场激光雷达探测回波进行计算分析显示，相较于尾流消散，涡核下沉运动对尾涡环量的计算精度影响更大，所以对涡核位置的精确计算能够有效提高尾涡整体特征参数的估算精度。