基于正规基表示的有限域GF(28)上椭圆曲线点阵群的加密算法

刘海峰，卢开毅，梁星亮

(1.陕西科技大学电气与信息工程学院，陕西 西安，710021；2．陕西科技大学文理学院，陕西 西安,710021)

椭圆曲线密码体制(elliptic curve cryptosystem，ECC)可以使用比RSA密码体制短得多的密钥得到相同的安全性，是一种安全性高、计算量小、所需带宽要求低的非对称加密算法，可以在很大程度上减少处理负荷，被广泛用于硬件实现的加密系统中[1-3]。有限域GF(2m)上的基本运算涉及到多项式的模乘运算和求逆运算[4]，因此有限域GF(2m)上椭圆曲线比有限域GF(P)上椭圆曲线具有更高的复杂性，从而也有其独特的安全性优势，受到信息安全界的大量关注。

有限域GF(28)上椭圆曲线的点可以通过正规基的形式进行表示，有利于算法的硬件实现，并且由于同一元素在不同正规基下的表示形式并不一定相同，使得攻击者获得有效信息的难度更大，为此本文运用群论的概念构造有限域GF(28)上的椭圆曲线点阵群，将其应用于分组加密算法当中，从而得到基于有限域GF(28)上正规基表示的椭圆曲线点列的分组密码系统。

1 有限域GF(28)上椭圆曲线概述

1.1 有限域GF(28)上的基本运算

GF(28)是一种特殊的有限域，其具有28个元素，每个元素都可以表示为8位二进制数，并可以将每个元素惟一地映射为一个系数为0和1的8次以下的一元多项式，其有限域上的多项式加法和乘法等运算具有封闭性，在密码学、信息安全等领域都是很重要的数学工具。有限域GF(28)与GF(2)[x]/p(x)上的元素及元素间相应的运算具有一一对应的性质，其中GF(2)[x]是二元域GF(2)上的一元多项式的全体集合，p(x)是GF(2)上的一个8次不可约多项式，因此一般来说，讨论有限域GF(28)就等价于讨论有限域GF(2)[x]/p(x)。

(2)a(x)-b(x)=a(x)+b(x)。

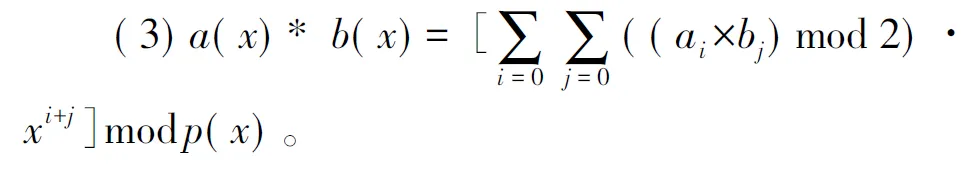
(4)a(x)-1:当且仅当a(x)*a(x)-1=1。

(5)a(x)/b(x)=a(x)*b(x)-1。

1.2 有限域GF(28)上椭圆曲线的定义[5]

对于有限域GF(28)上的椭圆曲线，使用变元和系数均在有限域GF(28)上取值的三次方程，并利用有限域GF(28)中的算术运算规则进行计算。有限域GF(28)上适合于椭圆曲线密码应用的三次方程为:

y2+xy=x3+ax2+b，

其中的变元x和y以及系数a和b都是有限域GF(28)中的元素，且所有的计算均在GF(28)中进行。椭圆曲线上的所有整数对(x,y)和无穷远点O组成集合E28(a,b)，当b≠0时则可基于集合E28(a,b)定义一个有限的阿贝尔群。

1.3 有限域GF(28)上椭圆曲线的运算规则

有限域GF(28)上椭圆曲线上点的运算规则如下。对所有的点P,Q∈E28(a,b)：

(1)P+O=P，其中O为无穷远点。

(2)若P=(xP,yP)，则有P+(xP,xP+yP)=O。因此-P=(xP,xP+yP)为P的负元。

(3)若P=(xP,yP)，Q=(xQ,yQ)，且有P≠Q，P≠-Q，则R=P+Q=(xR,yR)由以下规则确定：

xR=λ2+λ+xP+xQ+a，

yR=λ(xP+xR)+xR+yP，

其中

λ=(yQ+yP)(xQ+xP)-1。

(4)若P=(xP,yP)，则R=2P=(xR,yR)由以下规则确定：

xR=λ2+λ+a，

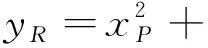
其中

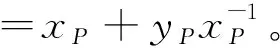
1.4 椭圆曲线的离散对数难题

使用椭圆曲线作为公钥密码体制的基础是定义在有限域GF(2m)上椭圆曲线的点集可以构成阿贝尔群，由此可以定义其上的离散对数。椭圆曲线的离散对数难题，即在已知椭圆曲线上一点P和Q=kP时(其中P,Q∈E2m(a,b))，要计算k的值就只能找到指数级时间复杂度的算法，而无法用多项式时间复杂度的算法进行求解[6]。

2 基于有限域GF(28)上点阵群的椭圆曲线加密算法设计

2.1 密码学意义上点阵群的构建

本文在杨军[7]提出的椭圆曲线点阵群概念的基础之上，构建一种具有密码学意义的有限域GF(28)的椭圆曲线点阵群[8]。令K=F28为有限域GF(28)。E/K为定义在K上的椭圆曲线，E(K)是椭圆曲线E/K上所有的点连同无穷远点O构成的有限加群，考虑集合G={A|A∈Mr×s(E(K))}，其中Mr×s(E(K))表示元素是E(K)上点的r×s规模之矩阵的集合。

定义1(点阵相等) 设P,Q∈G，其中Pij是矩阵P第i行第j列的元素，Qij是矩阵Q的第i行第j列的元素，若有Pij=Qij(i=1,2,…,r;j=1,2,…,s)，则称P和Q相等，记为P=Q。

定义2(点阵加法) 设P,Q∈G，其中Pij是矩阵P第i行第j列的元素，Qij是矩阵Q的第i行第j列的元素，若R=P+Q，则有Rij=Pij+Qij(i=1,2,…,r;j=1,2,…,s)。

定义3(点阵负元) 设P,Q∈G，其中Pij是矩阵P第i行第j列的元素，Qij是矩阵Q的第i行第j列的元素，若O=P+Q，其中O为元素全为无穷远点O的零阵，也即O=Pij+Qij(i=1,2,…,r;j=1,2,…,s)，则称P为Q的负元(或Q为P的负元)，记为P=-Q(或Q=-P)。

下面证明有限域GF(28)上椭圆曲线上的点阵关于加法“+”构成群〈G,+〉。

(1)封闭性：设P,Q∈G，则显然P+Q=([Pij]+[Qij])∈G成立。

(2)结合律：设P,Q,R∈G，则显然有(P+Q)+R=([Pij]+[Qij])+[Rij]=[Pij]+([Qij]+[Rij])=P+(Q+R)。

(3)存在单位元：设P∈G，则O+P=P+O。

(4)每个元都有逆元：设P∈G，则点阵P中的元素Pij都是椭圆曲线上的点，因此必然存在椭圆曲线上的点Qij使得有Pij+Qij=O，因此点阵Q=[Qij]∈G。

根据以上的证明，可得有限域GF(28)上椭圆曲线上的点构成的集合满足群的概念，可以构造密码学意义上的椭圆曲线点阵群。

2.2 椭圆曲线加密算法设计

假设A要给B发送消息，则双方需要先确定好有限域GF(28)上的不可约多项式p(x)以及椭圆曲线的参数a和b，从而得到相应椭圆曲线上点的集合E28(a,b)。然后选取基点G，并通过双方的私钥nA、nB分别产生A、B双方的公钥PA=nAG、PB=nBG。

(2)解密阶段：加密阶段A使用了B的公钥PB，B要对密文进行解密，则需要用密文点阵Cm的第二列减去第一列与B的私钥nB的乘积，从而实现解密，也即有Pm+kPB-nB(kG)=Pm+k(nBG)-nB(kG)=Pm。

A通过将点阵kPB与点阵Pm相加来伪装消息，因为只有A知道k，所以即使PB是公钥，除了A之外任何人都不能去除伪装kPB，鉴于椭圆曲线的离散对数难题，攻击者要想从G和kG中求出k是很难的，并且在使用了基于点阵群的椭圆曲线之后，每次分组加密时的k是一个向量而不是一个单独的数值，因此要同时破解k的t个分量难度更大，从而攻击者想要恢复消息明文的难度也越大。

3 基于有限域GF(28)上点阵群的椭圆曲线加密算法实现

3.1 有限域GF(28)上元素的正规基表示

有限域GF(28)上元素的正规基表示[9]也即在8次不可约多项式p(x)确定之后，可以找到有限域上的一个生成元g，使得有p(g)=0，并且GF(2)[x]/p(x)-{0}的元素可以表示为{g0,g1,g2,…,g28-1}，其中生成元g∈GF(28)。通过正规基的表示，特别是当正规基是最优正规基[10]的时候，有限域GF(28)上的运算可以得到很大程度的简化。

(1)平方运算：平方运算可以简化成循环移位运算，从而有利于硬件实现。

(2)模逆运算：通过分治法，求逆运算可以转化为乘法运算和移位运算的结合。

(3)模乘运算：如果选择的正规基是最优正规基，则可以采用效率更高的方法实现模乘运算。

由于有限域GF(28)上的模乘运算和模逆运算相对于有限域GF(p)上的运算更为复杂，而将该域上的元素用正规基的形式表示有利于提高计算效率，因此目前基于有限域GF(2m)上的快速算法仍然是研究的热点问题。

3.2 椭圆曲线加密算法实现

本文选取8次不可约多项式p(x)=x8+x5+x3+x2+1，并选取有限域GF(2)[x]/p(x)上的一个生成元g=x，可以得到g在模不可约多项式p(x)下各次方幂的运算结果，如表1所示。

由表1可知，正规基g=x在模p(x)下的1～255次方幂刚好可以生成GF(2)[x]/p(x)-{0}上的所有元素一次且仅一次(其中g0=g255)。这里选取椭圆曲线方程的参数为a=g8=x5+x3+x2+1，b=g0=1，通过计算，可以得到此参数条件下椭圆曲线E28(g8,1)上基于生成元g的方幂表示的总共287个点，如表2所示，其中(x,y)表示实际椭圆曲线上的点(gx,gy)，(′E0′, 0)表示实际椭圆曲线上的点(0,1)。其对应的椭圆曲线E28(g8,1)上的点如图1所示。

表1 模p(x)下生成元g的各次方幂

表2 椭圆曲E28(g8,1)上基于生成元g的方幂表示的287个点

图1 椭圆曲线E28(g8,1)上的点

从图1可以看出，同一列上只有两个互为负元的点，即除了无穷远点O以外，其他的点都是成对出现的。本文选取287个互异的可见字符进行字符编码，如表3所示，使表3中的字符与表2中287个点建立一一对应的双射关系。

表3 字符编码表

注：space表示空格符。

假设要加密的字符串为M=hello,It’snicetomeetyou。首先，通过字符与椭圆曲线上点的对应关系，可以得到明文字符串的字符所对应的点分别为(2,104)，(240,65)，(241,52)，(241,52)，(38,68)，(11,90)，(′E0′, 0)，(55,6)，(210,242)，(223,182)，(210,240)，(′E0′, 0)，(3,153)，(225,245)，(1,183)，(240,65)，(′E0′, 0)，(210,242)，(38,68)，(′E0′, 0)，(3,180)，(240,65)，(240,65)，(210,242)，(′E0′, 0)，(227,142)，(38,68)，(4,197)。然后，将明文消息M分成4组，每组7个字符，可以得到M=M1+M2+M3+M4，选择基点G=(g1,g183)，得到G点的阶order=48(即有(n·order)G=O，其中O为无穷远点)，并随机生成具有7个分量的整数向量k=30 7 128 201 13 97 58，设B的私钥为nB=34，则加密方A通过B的公钥PB=nBG=(28,172)对消息分组进行加密Cm={kG,Pm+kPB}，最后可得加密后密文消息为C=C1+C2+C3+C4，其中：C1=ΦУΩΨⅰⅶⅳ┤Яс∧yi;C2=9У∪Ψ0ⅶA┤AcШуΨ;C3=┤УΩΨ⋮ⅶШ┤ЯсууⅨ;C4=vУΩΨnⅶ↓┤jc!Yσ。从加密结果来看，显然，当明文点所对应的k值相同时，其加密之后的密文点对的第一个分量也相同，因此符合预期。加密后的密文点对所对应的生成元g的方幂表示如表4所示，其中(x,y)表示实际椭圆曲线上的点(gx,gy)。

解密时B先将密文点对的两个相邻分量分别转换成椭圆曲线E28(g8,1)上的点，然后用他的私钥nB=34来计算Cm2-nBCm1=Pm+kPB-nB(kG)=Pm即可得到明文所对应的椭圆曲线上的点，最后通过查表转换，即可得到解密后的明文M=hello, It’s nice to meet you。

表4 椭圆曲线E28(g8,1)上基于生成元g的方幂表示的密文点对

4 安全性分析

4.1 有限域GF(28)的丰富性

椭圆曲线加密算法的安全性首先表现在它所确定的有限域的丰富性。在有限域GF(28)中，当选取的8次不可约多项式p(x)不同时，得到的有限域也不相同，即一旦确定了有限群，可供选取的椭圆曲线是非常丰富的。通过计算可以得到多项式环GF(2)[x]上的8次不可约多项式共有30个，其降幂排列时对应的系数向量如表5所示，因此一共可以构成30个不同的有限域GF(2)[x]/p(x)。

表5 多项式环GF(2)[x]上所有8次不可约多项式的系数向量

4.2 随机点列的破解难度

4.3 正规基的非确定性

同一个有限域GF(2m)上可能会有多个不同的生成元，例如在有限域GF(24)上，选取多项式环GF(2)[x]上的4次不可约多项式为p(x)=x4+x+1时，可选择的生成元包括g1=x，g2=x+1，g3=x2，g4=x2+1，g5=x3+1，g6=x3+x+1，g7=x3+x2+1，g8=x3+x2+x，其在模p(x)下的1～15次方幂的系数向量如表6所示。

从表6中可以看出，不同生成元gi的1～15次方都可以生成GF(24)-{0}中的所有元素一次且仅一次，因此可知有限域GF(24)上的同一个元素在不同正规基下会有不同的表现形式，对于有限域GF(2m)来说，情况也类似，因此，只有在知道所选择的正规基g之后，才能将正规基形式表示的点(x,y)还原到真正的椭圆曲线上的点(gx,gy)，由于正规基选择的非确定性，从而使得基于正规基表示的椭圆曲线点阵群的加密算法有更高的安全性。

表6 模p(x)下的不同生成元各次方幂的系数向量

5 结语

椭圆曲线密码体制是现有公钥密码体制中单位比特加密强度最高的算法。有限域GF(28)上椭圆曲线的点可以通过正规基的形式来表示，本文在选定多项式环GF(2)[x]上的8次不可约多项式p(x)之后，将有限域GF(28)上的元素用所选择生成元g的正规基表示，使模逆运算和模乘运算等得以简化，提高了加密算法效率。运用群论的概念建立有限域GF(28)上的椭圆曲线点阵群，将其应用于分组加密算法中，从而构建了基于有限域GF(28)上正规基表示的椭圆曲线点列的分组密码系统，分析表明其具有较高的安全性。